Problem 2) Consider the following Maxwell Boltzmann distribution of molecular speeds: P(v) = 4( m 27kBT a) Check the last equation. b) Calculate the average of v. c) Calculate the average of v². mp² v²e2kBT To calculate average values for say f(v) (function of v) one just integrates f(v) with P(v)dv from zero to infinity = P(v)f(v)dv, where signifies average of f(v). Of course, the distribution should be normalized: P(v)dv=1, (is a requirement for any probability distribution).
Problem 2) Consider the following Maxwell Boltzmann distribution of molecular speeds: P(v) = 4( m 27kBT a) Check the last equation. b) Calculate the average of v. c) Calculate the average of v². mp² v²e2kBT To calculate average values for say f(v) (function of v) one just integrates f(v) with P(v)dv from zero to infinity = P(v)f(v)dv, where signifies average of f(v). Of course, the distribution should be normalized: P(v)dv=1, (is a requirement for any probability distribution).
Related questions
Question
![**Problem 2: Consider the following Maxwell-Boltzmann distribution of molecular speeds:**
\[ P(v) = 4\pi \left( \frac{m}{2\pi k_B T} \right)^{\frac{3}{2}} v^2 e^{-\frac{mv^2}{2k_B T}} \]
To calculate average values for say \( f(v) \) (function of \( v \)), one just integrates \( f(v) \) with \( P(v) dv \) from zero to infinity \( \langle f(v) \rangle = \int_0^\infty P(v) f(v) dv \), where \( \langle f(v) \rangle \) signifies the average of \( f(v) \). Of course, the distribution should be normalized: \(\int_0^\infty P(v) dv = 1\), (this is a requirement for any probability distribution).
**Tasks:**
a) Check the last equation.
b) Calculate the average of \( v \).
c) Calculate the average of \( v^2 \).
d) Calculate from c) the RMS (Root Mean Square) value of the speed.
e) Calculate the most probable value of \( v \).
f) Square the results of b, d, and e and rank them from smallest to the largest value.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F09613d8c-4cef-4639-a65c-ee2add319cba%2Ffe920d0c-0f3d-47a4-b80b-a19c00c74e1d%2Flm0d07g_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 2: Consider the following Maxwell-Boltzmann distribution of molecular speeds:**
\[ P(v) = 4\pi \left( \frac{m}{2\pi k_B T} \right)^{\frac{3}{2}} v^2 e^{-\frac{mv^2}{2k_B T}} \]
To calculate average values for say \( f(v) \) (function of \( v \)), one just integrates \( f(v) \) with \( P(v) dv \) from zero to infinity \( \langle f(v) \rangle = \int_0^\infty P(v) f(v) dv \), where \( \langle f(v) \rangle \) signifies the average of \( f(v) \). Of course, the distribution should be normalized: \(\int_0^\infty P(v) dv = 1\), (this is a requirement for any probability distribution).
**Tasks:**
a) Check the last equation.
b) Calculate the average of \( v \).
c) Calculate the average of \( v^2 \).
d) Calculate from c) the RMS (Root Mean Square) value of the speed.
e) Calculate the most probable value of \( v \).
f) Square the results of b, d, and e and rank them from smallest to the largest value.
Expert Solution
Step 1
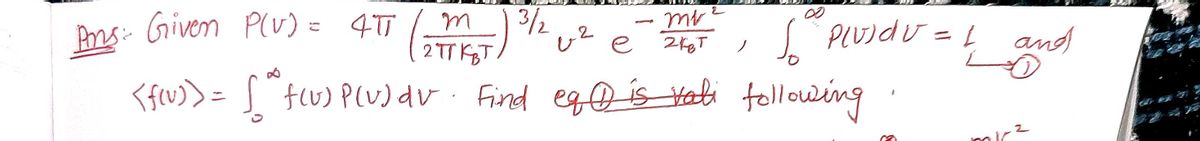
Step by step
Solved in 2 steps with 2 images
