• prove that the force is Conserved •then find the potential function
Q: If the speed at x = 1, v(x = 1) = 3 m/s then the speed at x 0, v(x=0) is:
A:
Q: position is located at . Consider the following potential V(r) = 31² + 4r + 3. The equilibrium and…
A:
Q: Suppose that an electric charge flows through a straight conductor (of cross section So) due to an…
A:
Q: In a plane region the volumetric charge density grows linearly along the direction. We can conclude…
A: Given that the volume charge density grow lenearly along X- axes. Hence let volume charge density=…
Q: (d) When a conservative force does negative work, which way do the force and infinitesimal…
A: (d) When a conservative force does negative work, the force and infinitesimal displacement vectors…
Q: question 47. can u explain step by step
A: Given values, Mass of sphere-1, m1=0.5 Kg Mass of sphere-2, m2=1.5 Kg Before collision: Velocity of…
Q: Compute for the electric potential at A(-3,6,4) given the electric field due to a uniform infinite…
A:
Q: With what initial speed should a positive charge, +q, of mass mbegiven such that if starting…
A:
Q: Find the electrical potential at point P. 2R R. 3R
A: Given, The electric potential for a ring of radius a at the same point (distance x) is: V = 14πεoqr2…
Q: Q 2: A particle, moving in the potential Vx)--Fx, travels from the point x 0 to the point x a in a…
A: Given that the particle is moving in potential given by, V(x)=-Fx (1) As it moves from x=0 to…
Q: A simple pendulum is composed of a bob of mass m attached to a string of length l. The tension at an…
A: We’ll answer the first question since the exact one wasn’t specified. Please submit a new question…
Q: Consider the "step" potential: 0. =1 (a) Calculate the reflection coefficient, for the case E 0.…
A:
Q: i) E can be expressed as a gradient of a scalar (V). What property of E allows us to do that? i)…
A:
Q: Determine whether the vector field is conservative and, if so, find the general potential function.…
A: Write the expression of vector field. F=coszi+2y3j-xsinzk
Q: Consider the potential distribution V = 5r² sin 0 sin ø. Find: Py everywhere i. ii. The energy…
A: (i). The relation between scaler potential and volume charge density is given by the poissions…
Q: Example 2 Aparticle moves in a linear potential V (x)=-ka, (i.e. under a constant force condition).…
A:
Q: The radial force is given as follows: F = (-k/r^2) r^ Calculate V XF =? Then find the potential…
A: The curl of a operator in spherical coordinated is given by, ∇×A→=r^ 1rsin(Θ)∂∂ΘAϕsin(Θ)-∂AΘ∂ϕ +Θ^…
Q: The force vector is conservative or non conservative
A: Given that:- F→=(x2yz)i^+(-xyz2)k^ For a conservative force, its curl is zero.
Q: Consider the following potential V(x) = 3r² + 4x + 3. The equilibrium position is located at %3D and…
A: Given : V(x) = 3x2+4x+3 We have to calculate the equilibrium position and whether it is stable,…
Q: Take a square configuration of point charges, two positive and two negative, all of the same…
A: Given charge distribution: Where, q is magnitude of all charges and…
Q: Consider a space with a constant electric field pointing up E = Ek, with E = 1 (in units of V/m).…
A: Given: E=1k^ V/m, r1=(1,3,3), r2=(3,0,4) The electric field in a region is defined by the negative…
Q: A thin rod has total charge 3W spread out uniformly over its length H. The distance between point A…
A:
Q: What is vactor quantity
A:
Q: the linear charge density of electric charge in a wire of length L, is given by the function g = kx…
A: Given: Length of wire is L Function g=kx
Q: The charge density on a disk of radius R = 11.8 cm is given by o = ar, with a = 1.36 µC/m³ and r…
A:
Q: Show that the force F = -k(yz, rz, ry), where k is a constant, is conservative and determine the…
A:
Q: a) What is the general expression of force resulting from the L-J potential? b) At what value of…
A: The force Fx corresponding to a potential Ux is given by, Fx = - dUdx Given, Ux = 4U0x0x12 - x0x6'…
Q: • A block of mass m = 0.88 kg is connected to a spring of forceconstant k = 845 N>m on a smooth,…
A:
Q: Consider the geometry shown in the figure below. The lengths of the plates in the x and z directions…
A:
Q: Please Find the critical points, evaluate the stability of them and sketch the inn phase plane.…
A:
Q: A particle with charge g4 = -6.35 µC is located at (0, 3.25 cm) and a second particle with charge gR…
A: Given : qA = -6.35 µC = -6.35 x 10-6 C qB = 3.00 µC = 3.00 x 10-6 C
Q: A circular disk with radius R has a constant surface charge density, o. ) Determine the electric…
A: From ∆rl OPQPQ2=OP2+OQ2PQ2=Z2+R2PQ = Z2+R2So potential at P are…
Q: BL Using the general expression V(r,0) = E2o (4,r' +)P(cose) for the potential at a %3D distance r…
A: Potential inside and outside spherical shell
Q: Separation of Variables: Cartesian coordinates A rectangular metal tube (its height extends from z =…
A:
Q: (0, 0,0) and the 5. The point o is the origin of the coordinate system, o = coordinates of b are b =…
A: (a) Given: The electric potential at point o is 0. The electric potential at point b is -∫obE→·dr→.…
Q: There are 12 cqually like charges arranged in a clock face pattern of radius R. Determine then, if…
A:
Q: The electric potential of a charged conducting sphere (as well as a spherical shell) can be…
A:
Q: Consider an infinitely long, hollow duct with a square cross section, see Figure below. The sides of…
A:
Q: An object with charge q = -11.00 nC is placed in a region of uniform electric field and is released…
A: Given: Charge, q=-11 nC=-11×10-9 C Work done by the electric field, W=0.5 μJ=0.5×10-6 J Electric…
Q: Q3) Find the potential u(r, 9) inside a ring 1 <r < 2 if the potential on the inner boundary r = 1…
A:
Q: : Suppose the electric potential at (x, y) is given by f(x, y) = 0.5 Ln(xpow2 + ypow2) estimate the…
A:
Q: find where E = 0, given V(x,y) = 2xy - x^2-y. E is the electric field and V(x,y) is the potential.…
A: Given value--- V(x,y) = 2xy - x^2-y. We have to find--- value of x and y at which electric field…
Q: A particle is trapped in a potential well described by U(x) = 16x² – b, %3D with U in joules, x in…
A: Force on a particle with potential energy U is, F=-dU(x)dx ...................(1) Given Data…
For conservative force, the curl of force is zero.
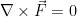
Conservative force can be written as
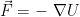
Where U = Potential function
Step by step
Solved in 3 steps with 8 images
