Answered: Q3) Find the potential u(r, 9) inside a… | bartleby

Related questions

Question

Q3) Find the potential u(r, 9) inside a ring 1 <r < 2 if the potential
on the inner boundary r = 1 is zero while on the outer boundary
r = 2 is given by 2 cos 39

Expert Solution

Step 1

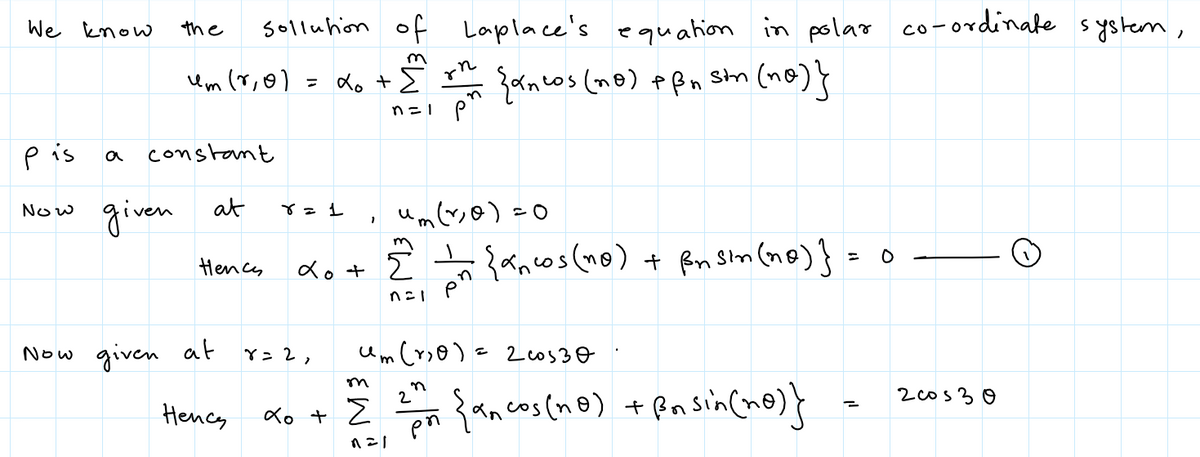
Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 2 images

SEE SOLUTION Check out a sample Q&A here

Blurred answer

Similar questions

Suppose we have an electric potential that is a function of z and the distance in the transverse plane, Vx2 + y?. In other words, o → ¢(rl,z). Show that the gradient can be written V¢ = dz Similarly, suppose we have a potential that is purely a function of the distance, r = from the origin. Show that the gradient can be written Vx2 + y2 + z², Vø = ar
An isolated conducting sphere of radius r1 = 0.20 m is at a potential of -2000V, with charge Qo. The charged sphere is then surrounded by an uncharged conducting sphere of inner radius r2 = 0.40 m, and outer radius r3 = 0.50m, creating a spherical capacitor. (a)Draw a clear physics diagram of the problem. (b) Determine the charge Qo on the sphere while its isolated. (c)A wire is connected from the outer sphere to ground, and then removed. Determine the magnitude of the electric field in the following regions: R<r1 ; re<R < r2; r2< R < r3; r3 < R (d) Determine the magnitude of the potential difference between the sphere and the conducting shell. (e) Determine the capacitance of the spherical capacitor.
What is the electric potential in volts (realative to zero at infinity) at the origin for a charge of uniform density 14.62 nC/m is distributed along the z axis from z=2,5 m to z=5.78 m Round your answer to 2 decimal places.
SSD_W06_04 0/3 points (graded) R. +Q B R. The figure above shows a solid insulating sphere of radius R2 with charge -Q (Q > 0) distributed uniformly throughout the volume. This sphere is centered within a thin spherical shell of radius R1; a charge +Q is distributed uniformly on the surface of the spherical shell. Very far away from the sphere and the spherical shell, the electric potential is zero. Use k for Coulomb's constant. At point A on the surface of the spherical shell, what is the electric potential VA? VA = Point B is on the surface of the sphere. What is the potential difference, VB – VẠ? VB - VA = Point C is at the center of the sphere. What is the potential difference, Vo - VB? Ve - VB =
E1.3
Consider a solid insulating sphere which has a total chargeof +3Q but is distributed as ρ(r) = βr, and has a radius of a. This issurrounded by a conducting shell that has a charge of −3Q placed onits outer surface. The inner radius is b and the outer radius is c. a) Determine β in terms of Q and a.b) Find the potential at all points in space
A thin rod extends along the x-axis from x = −a to x = a . The rod carries a positive charge +Q uniformly distributed along its length 2a with charge density λ, as shown in Figure attached. a) Use dV = 1/4πε0 ∫ dq/r to show that the electric potential at point P is given by: V(x) = (λ/4πε0) ln(x + a/x − a) b) What is the electric potential of the rod at x = 4a and x = 2a? c) What is the electric potential difference between x = 4a and x = 2a?
What is the electric potential in volts (relative to zero at infinity) at the origin for a charge of uniform density 13.97 nC/m is distributed along the z axis from z = 2.1 m to z = 6.45 m. Round your answer to 2 decimal places.
What is the electric potential in volts (relative to zero at infinity) at the origin for a charge of uniform density 11.46 nC/m is distributed along the z axis from z = 2.6 m to z = 6.12 m.
A cylindrical shell of radius R, and height his charged with charge that is uniformly distributed over it surface. To find the electric potential due to this shell at point Pa distance d from its right base we take, as an element, a thin ring that has a charge element: ut of dx Select one: O dq = o(2 TRdx) O dq = o(2 Trdr) O dq = p(TR?dx) dq = o(TR?dx) Two concentric conducting spherical shells of radii a and bare charged to a total charge Q. If the two shells are connected as shown. Which of the following is false? en 5 ete D out of REDMI NOTE 9 144 AI QUAD CAMERA
When an uncharged conducting sphere of radius a is placed at the origin of an xyz coordinate system that lies in an initially uniform electric fieldE = E, k, the resulting electric potential is V (x,y,z) = Vo for the points inside the sphere and V (x,y,z) = Vo – Egz + Ega³z (x² + y² + z²)3/2 for points outside the sphere, where V is the (constant) electric potential on the conductor. Use this equation to determine the x, y, and z components of the resulting electric field in the following regions. (Use the following as necessary: X, y, z, a, and Eo:)
The electric potential in a region of space varies as V=by/(a2+y2)V=by/(a2+y2). Determine the components of E→ Express your answers in terms of the variables a, b, and y separated by commas..

SEE MORE QUESTIONS