l. The mean score for 16 randomly selected boys is 136 with a standard deviation of 29, and the mean score of 13 randomly selected girls is 142 with a standard deviation of 27. At alpha equal 0.05, can you reject the researcher's claim? Assume the population are normally distributed and variances are equal. a. Set up the Hypotheses and indicate the claim H0: Ha: b. Decision rule Please show rejected region c. Computation
5. A teacher claims that the
a. Set up the Hypotheses and indicate the claim
H0:
Ha:
b. Decision rule Please show rejected region
c. Computation
d. Decision
e. Interpretation
Hi, the question have more than 3 parts. As per the guidelines I am obliged to answer first three parts only.
The researcher claims that the mean scores on a Mathematic assessment test for 7th grade boys and girls are equal. So null hypothesis will be that the mean scores on a Mathematic assessment test for 7th grade boys and girls are equal whereas alternative hypothesis will contradicts the claim that the mean scores on a Mathematic assessment test for 7th grade boys and girls are not equal.
Thus, the hypothesis will be:
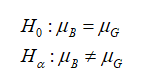
The tail of the test is two tailed. The critical value can be calculated from 0.05 level of significance and degree of freedom will be degree of freedom.
Thus the critical value will be:
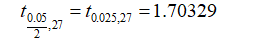
Thus, the rejection region is,
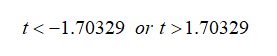
Step by step
Solved in 3 steps with 5 images









