Determine the reactions on the beam at A and B. 300 N/m 5 m 550 N/m 5 m. 5 m- 300 N/m B
Determine the reactions on the beam at A and B. 300 N/m 5 m 550 N/m 5 m. 5 m- 300 N/m B
Principles of Foundation Engineering (MindTap Course List)
9th Edition
ISBN:9781337705028
Author:Braja M. Das, Nagaratnam Sivakugan
Publisher:Braja M. Das, Nagaratnam Sivakugan
Chapter8: Vertical Stress Increase In Soil
Section: Chapter Questions
Problem 8.6P: Two line loads q1 and q2 of infinite lengths are acting on top of an elastic medium, as shown in...
Related questions
Question
Statics. A similar question is provided but I still don't get it. Please show fbd as the solved example

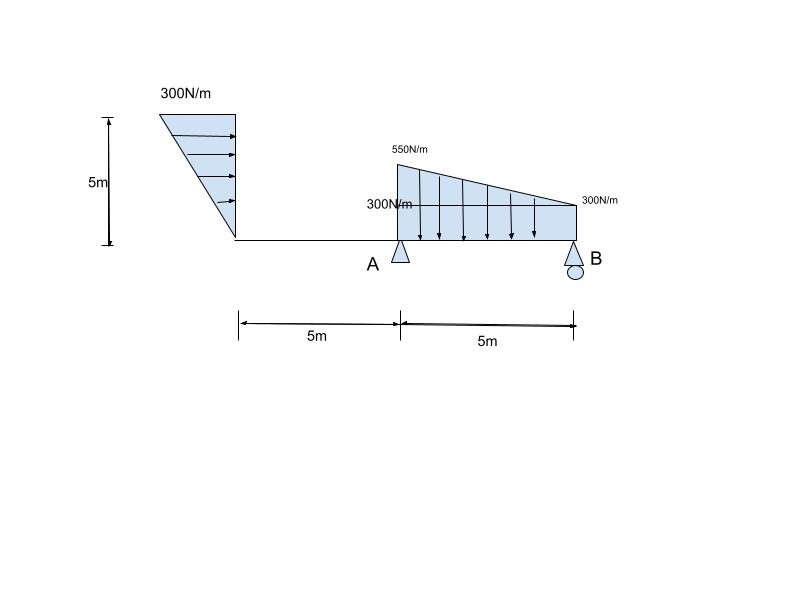
Transcribed Image Text:**Determine the reactions on the beam at A and B.**
In the diagram provided, there is a beam with a unique configuration and loading conditions. The beam is horizontal, transitioning into a vertical section at one end. The following are the details depicted:
- **Loads:**
- A uniformly distributed load of 300 N/m acts vertically downward on the vertical section of the beam (left side).
- The vertical section of the beam is 5 meters in height.
- A triangular distributed load acts across the horizontal section. The apex (zero) starts at the midpoint and increases to a maximum of 300 N/m at point B.
- The horizontal section's first half, nearest point A, is under a uniformly distributed load of 550 N/m pointing vertically downward.
- **Supports:**
- There are two supports: one at point A and another at point B. Point A appears to be a pin support which allows rotation but no translation, and point B appears to be a roller support which allows horizontal movement but no vertical movement.
- **Measurements:**
- The horizontal length is 10 meters in total, with support A located 5 meters from the start of the horizontal section and support B located at the far right end.
The problem invites analysis to determine the reaction forces at supports A and B, which are critical for assessing structural stability and ensuring safety under the given load conditions.
![### Problem Statement
1. The beam has a pin support at A, a roller support at B, and is subjected to a trapezoidal distributed load. What are the reactions at A and B?
### Diagram
- A beam is supported at two points: a pin support at point A and a roller support at point B.
- The beam is 4 meters long.
- The distributed load is trapezoidal in shape, ranging from 50 kN/m at point A to 25 kN/m at point B.
### Calculations
#### Sketch
- A free body diagram of the beam is drawn.
- The load is replaced by equivalent point loads representing the trapezoidal distribution.
#### Equations
1. Moment about A:
\[
\Sigma M_A = + B(4) - 100(2) - 50\left(\frac{4}{3}\right) = 0
\]
- Solving for B:
\[
B = 66 \frac{2}{3} \text{ kN}
\]
2. Vertical Force Equilibrium:
\[
\Sigma F_y = A + B - 50 - 100 = 0
\]
- Solving for A:
\[
A = 83 \frac{1}{3} \text{ kN}
\]
### Reactions at Supports
- Reaction at support A: \( A = 83 \frac{1}{3} \text{ kN} \)
- Reaction at support B: \( B = 66 \frac{2}{3} \text{ kN} \)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F56e31c7e-7756-4536-82bd-7b11459ca2a1%2Fc78864d1-8174-48ba-a76b-39b7f6ba8cf2%2F9ixymr_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem Statement
1. The beam has a pin support at A, a roller support at B, and is subjected to a trapezoidal distributed load. What are the reactions at A and B?
### Diagram
- A beam is supported at two points: a pin support at point A and a roller support at point B.
- The beam is 4 meters long.
- The distributed load is trapezoidal in shape, ranging from 50 kN/m at point A to 25 kN/m at point B.
### Calculations
#### Sketch
- A free body diagram of the beam is drawn.
- The load is replaced by equivalent point loads representing the trapezoidal distribution.
#### Equations
1. Moment about A:
\[
\Sigma M_A = + B(4) - 100(2) - 50\left(\frac{4}{3}\right) = 0
\]
- Solving for B:
\[
B = 66 \frac{2}{3} \text{ kN}
\]
2. Vertical Force Equilibrium:
\[
\Sigma F_y = A + B - 50 - 100 = 0
\]
- Solving for A:
\[
A = 83 \frac{1}{3} \text{ kN}
\]
### Reactions at Supports
- Reaction at support A: \( A = 83 \frac{1}{3} \text{ kN} \)
- Reaction at support B: \( B = 66 \frac{2}{3} \text{ kN} \)
Expert Solution
Step 1: Given data
A beam is loaded as follows
Step by step
Solved in 5 steps with 13 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning

Steel Design (Activate Learning with these NEW ti…
Civil Engineering
ISBN:
9781337094740
Author:
Segui, William T.
Publisher:
Cengage Learning

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781305081550
Author:
Braja M. Das
Publisher:
Cengage Learning

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning

Steel Design (Activate Learning with these NEW ti…
Civil Engineering
ISBN:
9781337094740
Author:
Segui, William T.
Publisher:
Cengage Learning

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781305081550
Author:
Braja M. Das
Publisher:
Cengage Learning

Principles of Geotechnical Engineering (MindTap C…
Civil Engineering
ISBN:
9781305970939
Author:
Braja M. Das, Khaled Sobhan
Publisher:
Cengage Learning

Residential Construction Academy: House Wiring (M…
Civil Engineering
ISBN:
9781285852225
Author:
Gregory W Fletcher
Publisher:
Cengage Learning

Engineering Fundamentals: An Introduction to Engi…
Civil Engineering
ISBN:
9781305084766
Author:
Saeed Moaveni
Publisher:
Cengage Learning