By employing the prescribed definitions of the raising and lowering operators pertaining to the one-dimensional harmonic oscillator: x = ħ - (â+ + â_) 2mw hmw p = i - (â+ − â_) 2 Compute the expectation values of the following quantities for the nth stationary staten. Keep in mind that the stationary states form an orthogonal set. [ 4m4ndx = 8mn a. The position of particle (x) b. The momentum of the particle (p). c. (x²) d. (p²) e. Confirm that the uncertainty principle is satisfied for all values of n
By employing the prescribed definitions of the raising and lowering operators pertaining to the one-dimensional harmonic oscillator: x = ħ - (â+ + â_) 2mw hmw p = i - (â+ − â_) 2 Compute the expectation values of the following quantities for the nth stationary staten. Keep in mind that the stationary states form an orthogonal set. [ 4m4ndx = 8mn a. The position of particle (x) b. The momentum of the particle (p). c. (x²) d. (p²) e. Confirm that the uncertainty principle is satisfied for all values of n
Related questions
Question
100%

Transcribed Image Text:By employing the prescribed definitions of the raising and lowering operators pertaining to
the one-dimensional harmonic oscillator:
x
=
ħ
2mω
-(â+ + â_)
hmw
ê = i
Compute the expectation values of the following quantities for the nth stationary staten.
Keep in mind that the stationary states form an orthogonal set.
2
· (â+ − â_)
[ pm 4ndx
YmVndx = 8mn
a. The position of particle (x)
b. The momentum of the particle (p).
c. (x²)
d. (p²)
e. Confirm that the uncertainty principle is satisfied for all values of n
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
how do you determine what the values of the rising and lowering operators are? (how did you get these values of a+ and a-)
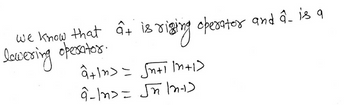
Transcribed Image Text:we know that ât is r
is rising operator and a_ is a
lowering operator.
â+In> = √n+in+1)
â-|m>= √n Inds
Solution