a) In this experiment you are measuring the change of potential AV over small displacement Ar. In the limit Ar 0, AV/Ar would give you the derivative of V with respect to r, which is the radial component of the electric field, E, (strictly speaking, with the minus sign). Take the natural logarithm of both sides of to show that In() can be represented as a linear function of In(7), In(A) = a In(r) + b. What are the constants a and b in terms of C and n?¹ AV Ar
a) In this experiment you are measuring the change of potential AV over small displacement Ar. In the limit Ar 0, AV/Ar would give you the derivative of V with respect to r, which is the radial component of the electric field, E, (strictly speaking, with the minus sign). Take the natural logarithm of both sides of to show that In() can be represented as a linear function of In(7), In(A) = a In(r) + b. What are the constants a and b in terms of C and n?¹ AV Ar
College Physics
11th Edition
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Raymond A. Serway, Chris Vuille
Chapter1: Units, Trigonometry. And Vectors
Section: Chapter Questions
Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...
Related questions
Question
Hello, I really need help with part A, part B, and Part C because I don't understand this problem can you help me with parts A, PART B, PART C, AND can you label which one is which.

Transcribed Image Text:Problem 3: It is postulated that the radial electric
field of a group of charges falls off as E, = C/r", where
Cis a constant, r is the distance from the center of the
group, and n is an unknown exponent. To test this
hypothesis, you make a field probe costisting of two
needle tips spaced Ar= 1.0 mm apart. You orient the
needles so that a line between the tips points to the
center of the charges, then use a voltmeter to read the
potential difference between the tips. After you take measurements at several distances from the center
of the group, your data are as given in the table. Use an appropriate graph of the data to determine the
constants C and n.
3
limit Ar →
a) In this experiment you are measuring the change of potential AV over small displacement Ar. In the
0, AV/Ar would give you the derivative of V with respect to r, which is the radial component
of the electric field, E, (strictly speaking, with the minus sign). Take the natural logarithm of both sides of
Ato show that In (AV) can be represented as a linear function of In(r), In(A) = aln(r) + b. What
are the constants a and b in terms of C and n?¹
b) Place the measurements In (AV) as a function of In(r) on the graph below.
2
1
7779 79 7
-3
-6
Distance, r (cm) Potential difference, AV (mV)
2.0
34.7
4.0
6.6
6.0
2.1
1.2
-7-1
S
8.0
10.0
-2
In(r)
0.6
2
AV
Note that here we use A=instead of E, = -A because the minus sign is already absorbed into the potential
difference values given in the table. The potential in this problem is decreasing with the distance, which means that the value
of potential at the tip of the probe that is farther from the center will be smaller than the potential of the closer tip.
c) If E, is indeed equal to C/r", your measurements should lic on a straight line (otherwise, you would
have to conclude that the field must be described by a different function). Can you connect the dots with
a straight line? Determine the constants C and n from this line (to do that, it is helpful to remember that
a line y = ax + b intersects y axis at the point y = b and x axis at the point x = -b/a).
Expert Solution
Step 1
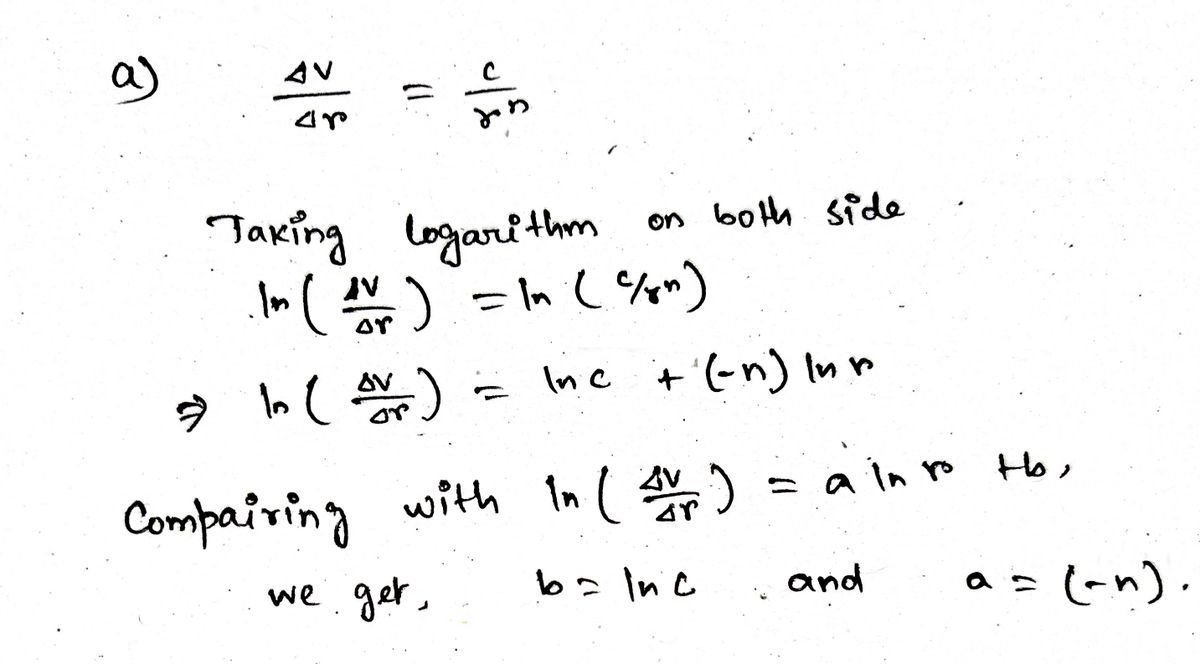
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:
9780321820464
Author:
Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:
Addison-Wesley

College Physics: A Strategic Approach (4th Editio…
Physics
ISBN:
9780134609034
Author:
Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:
PEARSON