12 तना State 2 Ita 77 State 1 datum
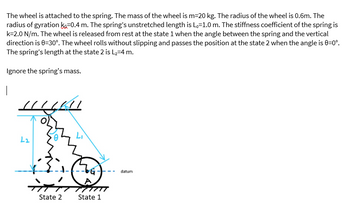
The wheel is attached to the spring. The mass of the wheel is m=20 kg. The radius of the wheel is 0.6m. The radius of gyration kG=0.4 m. The spring’s unstretched length is L0=1.0 m. The stiffness coefficient of the spring is k=2.0 N/m. The wheel is released from rest at the state 1 when the angle between the spring and the vertical direction is θ=30°. The wheel rolls without slipping and passes the position at the state 2 when the angle is θ=0°. The spring’s length at the state 2 is L2=4 m.
Ignore the spring's mass.
(1) If the datum for gravitational potential energy is set as shown below, the the gravitational potential energy of the wheel at the state 1 is___ N m(two decimal places)
(2) If the datum for gravitional potential energ is set as shown below, the gravitational potential energy of the wheel at the state 2 is___ N m (two decimal places)
(3) At state 1, how long the spring is stretched from its unstretched state (length difference):________(m) (two decimal places)
(4) The elastic potential energy of the spring at the potion 1 is_______(N·m) (two decimal places)
(5) At state 2, how long the spring is stretched from its unstretched state (length difference):________(m) (two decimal places)
(6) The elastic potential energy of the spring at the state 2 is_______(N·m) (two decimal places)
(7) The instantaneous center of zero velocity (IC) of the wheel at state 1 is
(8) The mass moment of inertial of the wheel about its mass center G is IG =_________(kg·m2 ) (two decimal places)
(9) The mass moment of inertial of the wheel about its IC center at state 1 is IIC =_________(kg·m2 ) (two decimal places)
(10) The total kinetic energy of the system at the state1 is:________ (N·m) (two decimal places)
(11) Apply the theory of work-energy to the whole system during state 1 and state 2, and calculate the angular velocity of the wheel at the state 2: _______(rad/s) (two decimal places)
12) Based on result from (11), the kinetic energy of the wheel at the state 2 is:______ (N·m) (two decimal places)

Step by step
Solved in 2 steps with 2 images

The wheel is attached to the spring. The mass of the wheel is m=20 kg. The radius of the wheel is 0.6m. The radius of gyration kG=0.4 m. The spring’s unstretched length is L0=1.0 m. The stiffness coefficient of the spring is k=2.0 N/m. The wheel is released from rest at the state 1 when the angle between the spring and the vertical direction is θ=30°. The wheel rolls without slipping and passes the position at the state 2 when the angle is θ=0°. The spring’s length at the state 2 is L2=4 m.
Ignore the spring's mass.
(5) At state 2, how long the spring is stretched from its unstretched state (length difference):________(m) (two decimal places)
(6) The elastic potential energy of the spring at the state 2 is_______(N·m) (two decimal places)
(7) The instantaneous center of zero velocity (IC) of the wheel at state 1 is
(8) The mass moment of inertial of the wheel about its mass center G is IG =_________(kg·m2 ) (two decimal places)
(9) The mass moment of inertial of the wheel about its IC center at state 1 is IIC =_________(kg·m2 ) (two decimal places)
(10) The total kinetic energy of the system at the state1 is:________ (N·m) (two decimal places)
(11) Apply the theory of work-energy to the whole system during state 1 and state 2, and calculate the angular velocity of the wheel at the state 2: _______(rad/s) (two decimal places)
12) Based on result from (11), the kinetic energy of the wheel at the state 2 is:______ (N·m) (two decimal places)