What is Depth First Search?
Depth-first search (DFS) also known as Depth First traversal is an algorithm used to traverse or search the nodes in a tree or graph data structure. Traversal usually means visiting all the nodes of a graph. DFS performs in a depth-ward manner. It uses a stack to remember the vertices it has visited. The search starts from the root node, where any arbitrary node is selected as a root node in a graph, and then each node is explored along each branch before performing backtracking. The DFS algorithm uses a recursive technique by following the idea of backtracking. DFS algorithm does this by performing an in-depth search of all the nodes by traversing in a forward direction. If the required node is not found, it starts backtracking to previously visited nodes.
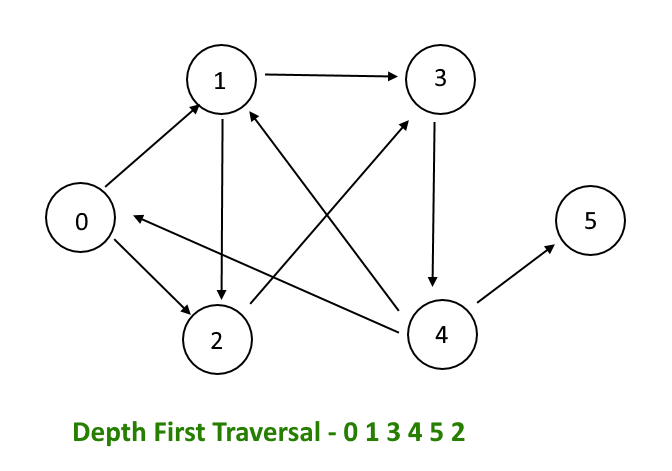
How Depth First Search(DFS) Works?
In a DFS algorithm, the traversal of a tree starts from a particular vertex that is often the root node. The traversing goes down to its child nodes and grandchild nodes till any end vertex is reached. As soon as the last vertex is reached from where no forward movement can be done that is no more child or neighbor is left to visit, the DFS algorithm starts backtracking to the node from where traversing can be continued to the nodes which have not been visited yet. The same process is repeated till all the nodes are traversed.
DFS implementation of any graph or tree marks each node/vertex as either Visited or Not Visited. The whole purpose of DFS is to mark all the nodes visited from which it may move in a forward or a backward direction. Also, the DFS algorithm does this in a manner to avoid cycles.
The DFS algorithm can be written as:
- Start: Put any random vertex of the graph on top of a stack.
- Add the node at top of the stack to the visited list.
- Mention all the adjacent nodes of the visited vertex in a list. The vertices which has not been visited should be added to the top of the stack.
- Repeat the above 2 steps until the stack is empty.
Methods of implementing DFS
Traversing can be done in three different manners based on the position of the node in a tree. A node can have three basic positions- Left(Pre), Right(Post), and Center(In). Following are the methods of implementing Depth First Search-
- Preorder
- Inorder
- Postorder
Preorder
The preorder DFS algorithm is the most standard. It works by visiting the root node/vertex first and keeps on moving to the left part of the tree(subtree) until no more child are unvisited, When all the node of the left subtree has been visited it moves to the right part of the tree and traverses the remaining nodes in a center-left-right manner. This strategy is commonly referred to as DLR (D-data, L-left child, R-right child).
Inorder
The Inorder depth-first search algorithm starts with the leftmost node of the left subtree instead of going down. It then reads the data stored in the root node before moving to the right subtree. As it reaches the right subtree, it again finds the leftmost child of the right subtree and continues to traverse in a left-center-right manner. This strategy is known as LDR.
Postorder
Postorder depth-first search algorithm works by traversing the leftmost leaf in the tree, then it jumps to the right subtree and starts traversing the left node of the right part. It keeps shifting from the left subtree and then at last visits the parent node of the tree in a left-right-center manner. This DFS strategy is called LRD.
Example of DFS
Let's understand DFS with the help of an example. Consider the following graph.
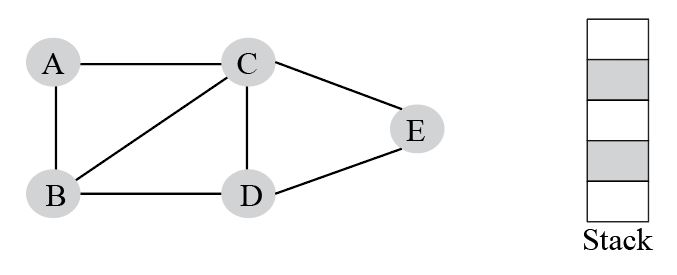
Step 1: Mark vertex A as a visited node, selecting it as a source node.
Now, push adjacent vertices of A, which are not visited yet to the top of the stack.
Visited list: A
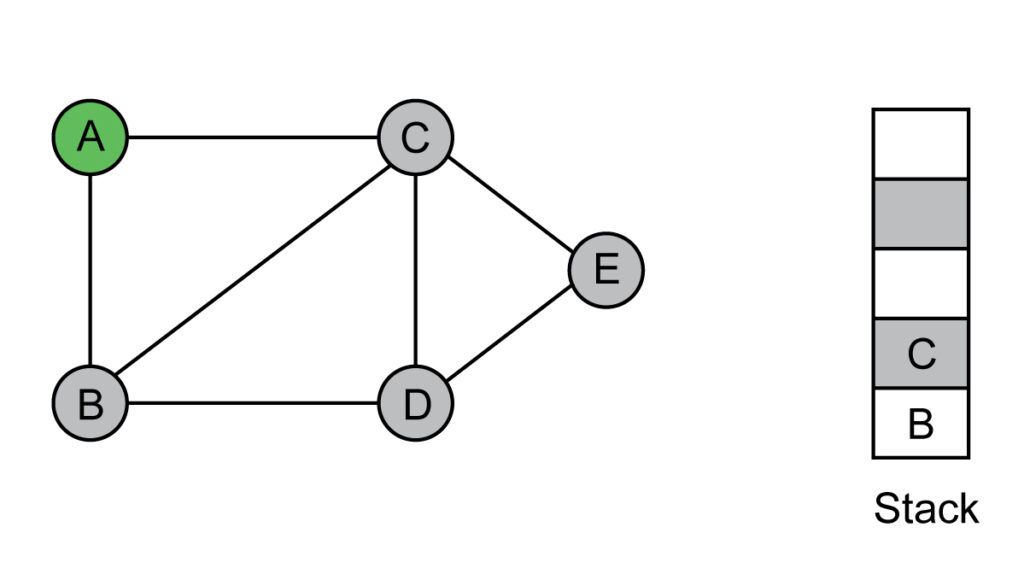
Step 2: Add the top vertex of the stack to the visited list.
Visited list: A, C
Now, push adjacent vertices of C, which are not visited yet to the top of the stack.
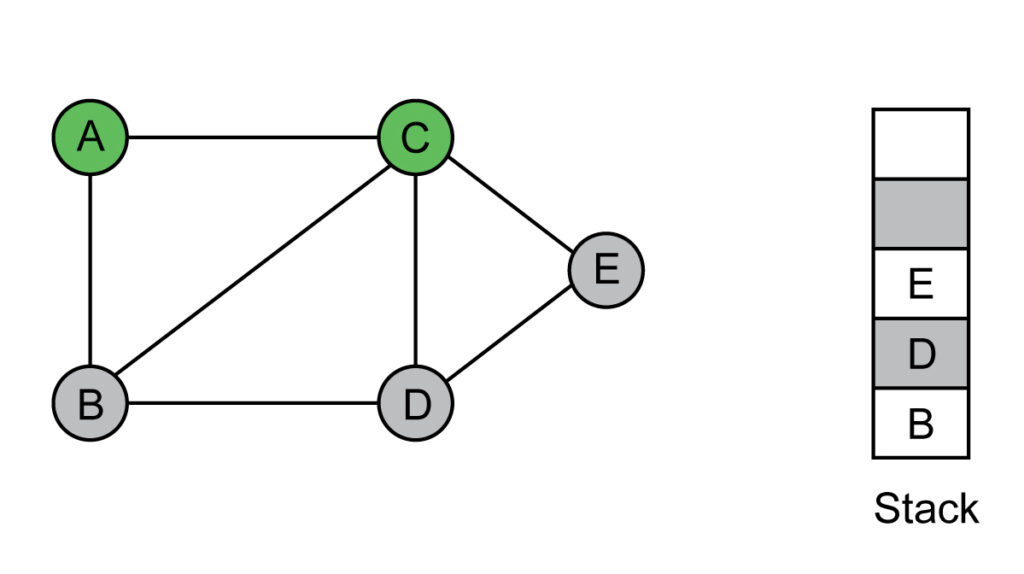
Step 3: Add E to the visited list and push the neighbors to the stack.
Visited list: A, C, E
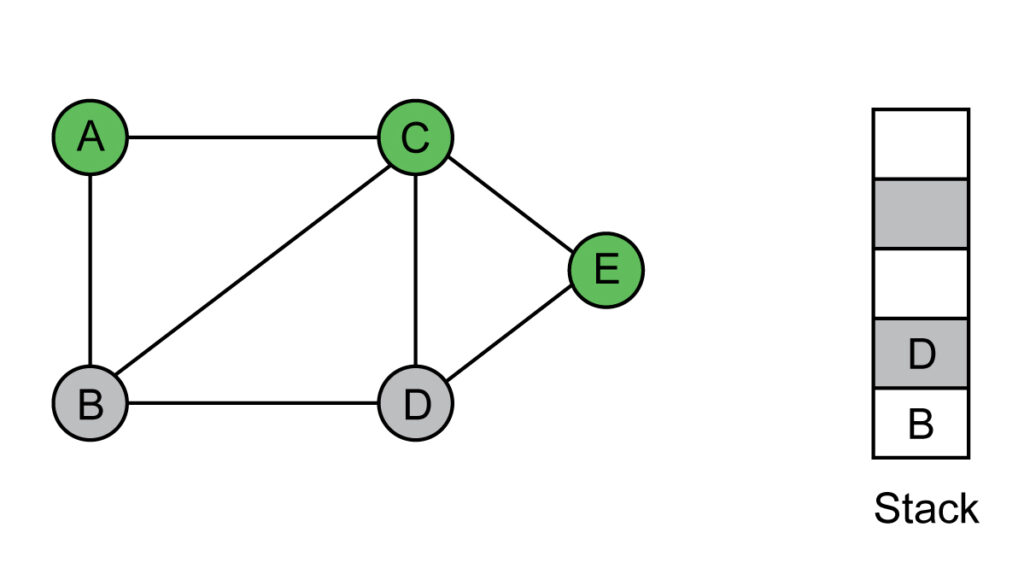
Step 4: Add D to the visited list, which is on top of the stack. Push D's neighbors, which are not visited yet. B is already in stack.
Visited list: A, C, E, D
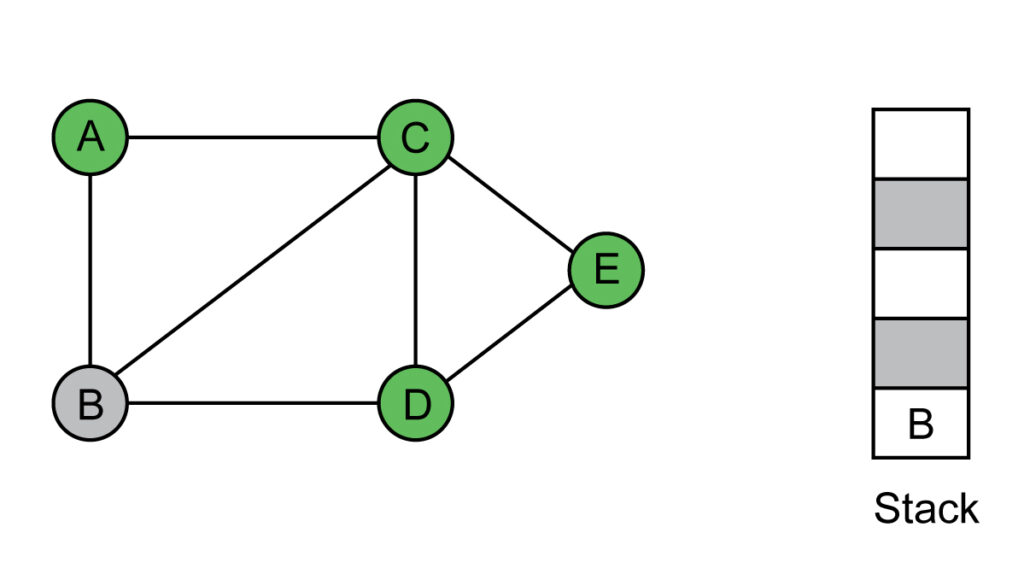
Step 5: Visit vertex B. Push the neighbors of B which are unvisited. No such vertices left in the graph.
Visited list: A, C, E, D, B
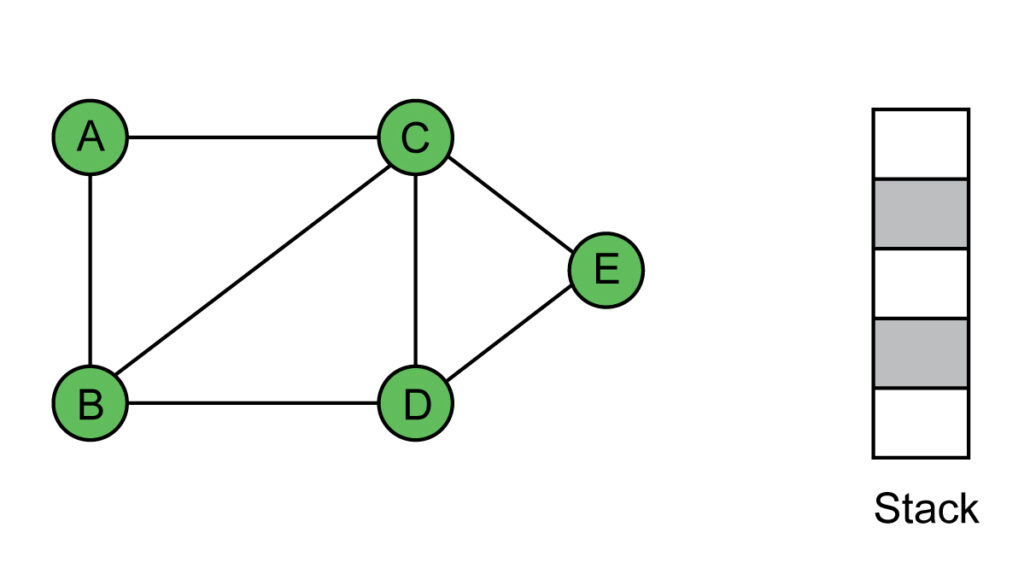
So BFS of the given graph is A-C-E-D-B. It is based on the order, in which the vertices are pushed on to the stack. If vertex C is pushed to the stack before vertex B, then B will be at the top of the stack and the DFS will be: A-B-D-E-C.
What is Depth First Search used for?
Wide applications of Depth First Search are
- Used in Topological sorting.
- Used for Scheduling problems.
- Used for Solving puzzles.
- Used for analyzing networks.
- Used for finding the path from one node to another.
- Used for finding the strongly connected components in a graph.
- Used for Cycle detection in graphs.
- Used to test, if a graph is bipartite or not.
DFS vs BFS
The breadth-first search algorithm is used to search or explore data structures such as graphs and trees. It starts from the root node and then explores all nodes at a certain level before moving on to the nodes of the next level.
The breadth-first search algorithm can be called less space-efficient than depth-first search because BFS maintains a priority queue of the entire traversal of vertex while DFS keeps only a few pointers at each level.
DFS is better than BFS while considering a tree. If a single answer is needed or when the depth of the tree can vary then only BFS is a good option. For example, to find the shortest path in a tree, we have to traverse the entire tree that is all vertex of a tree, then definitely DFS is a better option.
Complexity of Depth First Search
The time complexity of depth first search is O(V+E) where, V is the vertex count on the graph and E is the edge count in the graph. As an additional array of size V is needed to store the visited node information, the space complexity for DFS is O(V).
Common Mistakes
We use the DFS algorithm to search any node by traversing all the vertex/nodes in a depth-first manner but it is not necessary that every time we start a search, we may reach the goal node. Sometimes during the search using the forward or backtracking method, there are chances to enter into infinite loops. DFS may fail to find the shortest path in such cases.
Context and Applications
This topic is significant in the professional exams for both graduate and postgraduate courses, especially for:
- B.Tech in Computer Science
- M.Tech in Database System
- Bachelor's and Master's of Computer Applications
Related Topics
- Breadth-First Search (BFS)
- Traversing
- Types of search
- Spanning tree
Practice Problems
Q1. Which of the traversal in the Binary Trees is equivalent to Depth First Search?
a) In-order Traversal
b) Post-order Traversal
c) Level-order Traversal
d) Pre-order Traversal
Correct Answer- d) Pre-order Traversal
Explanation: In DFS, the nodes in the adjacent links are visited up to the last node and then backtrack to the node, so it is pre-order traversal.
Q2. In Depth First Search, how many times a node is visited?
a) 1
b) 2
c) 3
d) Equivalent to the degree of the node
Correct Answer- d) Equivalent to the degree of the node
Explanation: Each edge from a node will be visited to check if there is any node that is not visited in those paths.
Q3. Time Complexity of DFS is?
a) O(V/E)
b) O(V*E)
c) O(E)
d) O(V+E)
Correct Answer- d) O(V+E)
Explanation: The time complexity of DFS is based on the number of nodes (V) and edges (E).
Q4. Depth First Search of a graph is unique when the graph is __________
a) a Binary Tree
b) an n-ary Tree
c) a Linked List
d) a ternary Tree
Correct Answer- c) a Linked List
Explanation: The DFS will be unique when all nodes have only one successor. The linked list occupies this need.
Q5. Preorder depth-first search is also represented as
a} DLR
b) LDR
c) RLD
d) DRL
Correct Answer- a) DLR
Explanation: D- data, L-left, R- right is the order of traversal in preorder DFS.
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Depth First Search Homework Questions from Fellow Students
Browse our recently answered Depth First Search homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.