Chapter P.3, Problem 1P

Size and Life

Physicists look for simple models and general principles that underlie and explain diverse physical phenomena. In the first 13 chapters of this textbook, you’ve seen that just a handful of general principles and laws can be used to solve a wide range of problems. Can this approach have any relevance to a subject like biology? It may seem surprising, but there are general 'laws of biology“’ that apply, with quantitative accuracy, to organisms as diverse as elephants and mice.

Let’s look at an example. An elephant uses more metabolic power than a mouse. This is not surprising, as an elephant is much bigger. But recasting the data shows an interesting trend. When we looked at the energy required to raise the temperature of different substances, we considered specific heat. The “specific” meant that we considered the heat required for 1 kilogram. For animals, rather than metabolic rate, we can look at the specific metabolic rate, the metabolic power used per kilogram of tissue. If we factor out the mass difference between a mouse and an elephant, are their specific metabolic powers the same?

In fact, the specific metabolic rate varies quite a bit among mammals, as the graph of specific metabolic rate versus mass shows. But there is an interesting trend: All of the data points lie on a single smooth curve. In other words, there really is a biological law we can use to predict a mammal’s metabolic rate knowing only its mass M. In particular, the specific metabolic rate is proportional to M ^–0.25. Because a 4000 kg elephant is 160,000 times more massive than a 25 g mouse, the mouse’s specific metabolic power is (160,000)^0.25 = 20 times that of the elephant. A law that shows how a property scales with the size of a system is called a scaling law.

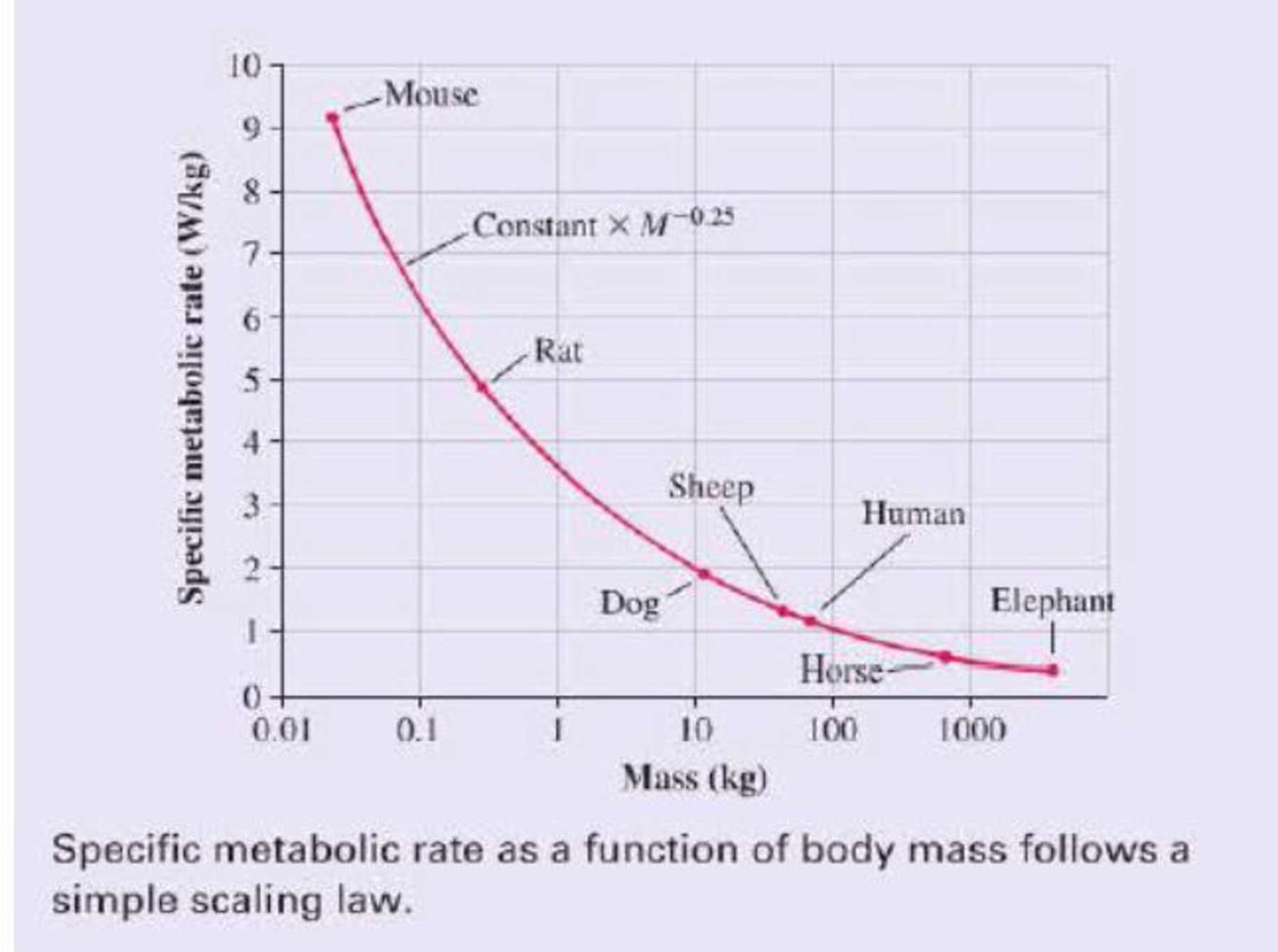
A similar scaling law holds for birds, reptiles, and even bacteria. Why should a single simple relationship hold true for organisms that range in size from a single cell to a 100 ton blue whale? Interestingly, no one knows for sure. It is a matter of current research to find out just what this and other scaling laws tell us about the nature of life.

Perhaps the metabolic-power scaling law is a result of heat transfer. In Chapter 12, we noted that all metabolic energy used by an animal ends up as heat, which must be transferred to the environment. A 4000 kg elephant has 160,000 times the mass of a 25 g mouse, but it has only about 3000 times the surface area. The heat transferred to the environment depends on the surface area; the more surface area, the greater the rate of heat transfer. An elephant with a mouse-sized metabolism simply wouldn't be able to dissipate heat fast enough—it would quickly overheat and die.

If heat dissipation were the only factor limiting metabolism, we can show that the specific metabolic rate should scale as M^–0.33quite different from the M^–0.25 scaling observed. Clearly, another factor is at work. Exactly what underlies the M^–0.25 scaling is still a matter of debate, but some recent analysis suggests the scaling is due to limitations not of heat transfer but of fluid flow. Cells in mice, elephants, and all mammals receive nutrients and oxygen for metabolism from the bloodstream. Because the minimum size of a capillary is about the same for all mammals, the structure of the circulatory system must vary from animal to animal. The human aorta has a diameter of about 1 inch; in a mouse, the diameter is approximately l/20th of this. Thus a mouse has fewer levels of branching to smaller and smaller blood vessels as we move from the aorta to the capillaries. The smaller blood vessels in mice mean that viscosity is more of a factor throughout the circulatory system. The circulatory system of a mouse is quite different from that of ail elephant.

A model of specific metabolic rate based on blood-flow limitations predicts a M^–0.25 law, exactly as observed. The model also makes other testable predictions. For example, the model predicts that the smallest possible mammal should have a body mass of about 1 gram—exactly the size of the smallest shrew. Even smaller animals have different types of circulatory' systems; in the smallest animals, nutrient transport is by diffusion alone. But the model can be extended to predict that the specific metabolic rate for these animals will follow a scaling law similar to that for mammals, exactly as observed. It is too soon to know if this model will ultimately prove to be correct, but it’s indisputable that there are large-scale regularities in biology that follow mathematical relationships based on the laws of physics.

The following questions are related to the passage "Size and Life" on the previous page.

A typical timber wolf has a mass of 40 kg, a typical jackrabbit a mass of 2.5 kg. Given the scaling law presented in the passage, we’d expect the specific metabolic rate of the jackrabbit to be higher by a factor of

1. A. 2
2. B. 4
3. C. 8
4. D. 16