The Greenhouse Effect and Global Warming
Although seasons come and go, on average the earth’s climate is very steady. To maintain this stability, the earth must radiate thermal energy—electromagnetic waves—back into space at exactly the same average rate that it receives energy from the sun. Because the earth is much cooler than the sun, its thermal radiation is long-wavelength infrared radiation that we cannot see. A straightforward calculation using Stefan's law finds that the average temperature of the earth should be –18°C, or 0°F, for the incoming and outgoing radiation to lie in balance.
This result is clearly not correct; at this temperature, the entire earth would be covered in snow and ice. The measured global average temperature is actually a balmier 15°C, or 59°F. The straightforward calculation fails because it neglects to consider the earth’s atmosphere. At visible wavelengths, as the figure shows, the atmosphere has a wide “window” of transparency, but this is not true at the infrared wavelengths of the earth’s thermal radiation. The atmosphere lets in the visible radiation from the sun, but the outgoing thermal radiation from the earth sees a much smaller “window.” Most of this radiation is absorbed in the atmosphere.
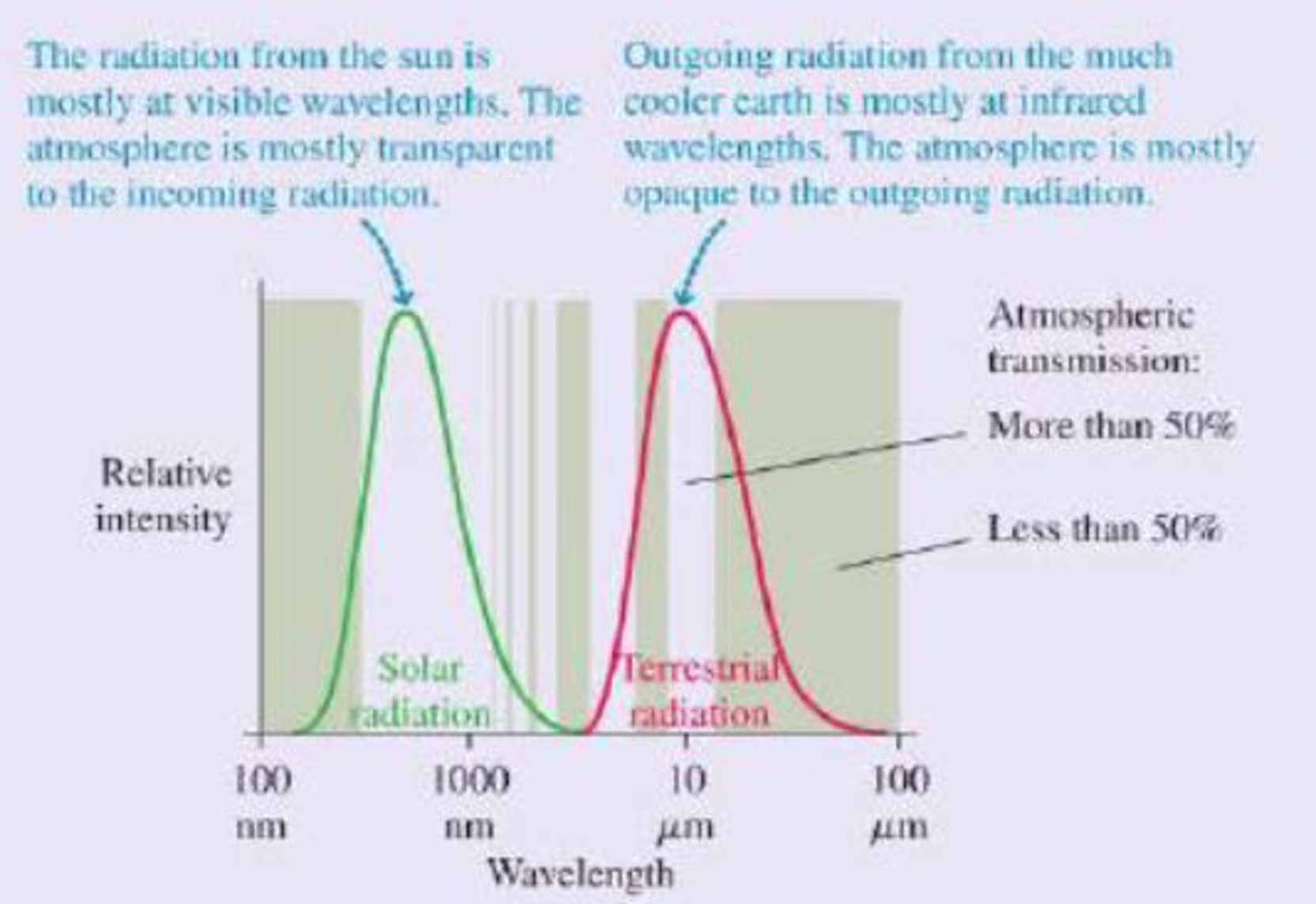
Thermal radiation curves for the sun and the earth. The shaded bands show regions for which the atmosphere is transparent (no shading) or opaque (shaded) to electromagnetic radiation.
Because it’s easier for visible radiant energy to get in than for infrared to get out, the earth is warmer than it would be without the atmosphere. The additional warming of the earth’s surface because of the atmosphere is called the greenhouse effect. The greenhouse effect is a natural part of the earth’s physics; it has nothing to do with human activities, although it’s doubtful any advanced life forms would have evolved without it.
The atmospheric gases most responsible for the greenhouse effect are carbon dioxide and water vapor, both strong absorbers of infrared radiation. These greenhouse gases are of concern today because humans, through the burning of fossil fuels (oil, coal, and natural gas), are rapidly increasing the amount of carbon dioxide in the atmosphere. Preserved air samples show that carbon dioxide made up 0.027% of the atmosphere before the industrial revolution. In the last 150 years, human activities have increased the amount of carbon dioxide by nearly 50%, to about 0.040%. By 2050, the carbon dioxide concentration will likely increase to 0.054%, double the pre-industrial value, unless the use of fossil fuels is substantially reduced.
Carbon dioxide is a powerful absorber of infrared radiation. And good absorbers are also good emitters. The carbon dioxide in the atmosphere radiates energy back to the surface of the earth, warming it. Increasing the concentration of carbon dioxide in the atmosphere means more radiation: this increases the average surface temperature of the earth. The net result is global warming.
There is strong evidence that (he earth has warmed nearly 1°C in the last 100 years because of increased greenhouse gases. What happens next? Climate scientists, using sophisticated models of the earth’s atmosphere and oceans, calculate that a doubling of the carbon dioxide concentration will likely increase the earth’s average temperature by an additional 2°C (≈ 3°F) to 6°C (≈9°F) There is some uncertainty in these calculations; the earth is a large and complex system. Perhaps the earth will get cloudier as the temperature increases, moderating the increase. Or perhaps the arctic ice cap will melt, making the earth less reflective and leading to an even more dramatic
But the basic physics that leads to the greenhouse effect, and to global warming, is quite straightforward. Carbon dioxide in the atmosphere keeps the earth warm; more carbon dioxide will make it warmer. How much warmer? That’s an important question, one that many scientists around the world are attempting to answer with ongoing research. But large or small, change is coming. Global warming is one of the most serious challenges facing scientists, engineers, and all citizens in the 21st century.
The following questions are related to the passage “The Greenhouse Effect and Global Warming” on the previous page.
The thermal radiation from the earth’s surface peaks at a wavelength of approximately 10 μm. If the surface of the earth warms, this peak will
- A. Shift to a longer wavelength.
- B. Stay the same.
- C. Shift to a shorter wavelength.
Want to see the full answer?
Check out a sample textbook solution
Chapter P Solutions
College Physics: A Strategic Approach (4th Edition)
Additional Science Textbook Solutions
Microbiology with Diseases by Body System (5th Edition)
Human Anatomy & Physiology (2nd Edition)
Microbiology: An Introduction
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Human Physiology: An Integrated Approach (8th Edition)
Campbell Biology (11th Edition)
- A shot putter releases a shot at 13 m/s at an angle of 42 degrees to the horizontal and from a height of 1.83 m above the ground. (Note: For each question draw a diagram to show the vector/s. Show all the step and provide units in the answers. Provide answer to 2 decimal places unless stated otherwise.) Calculate and answer all parts. Only use equations PROVIDED:arrow_forward"looks" like a particle.) ...32 GO In Fig. 22-55, positive charge q = 7.81 pC is spread uni- formly along a thin nonconducting rod of length L = 14.5 cm. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance R = 6.00 cm from the rod along its perpendicular bisector? R y Р + + + + + + + + +-× L Figure 22-55 Problem 32.arrow_forward1) A horizontal wire carrying current I in +x direction on the x-axis from x=0 to x=2 2) A vertical wire carrying current I upward at along the x=2 line from y=0 to y=8 3) A diagonal straight wire started at the origin and it ends at y=8 x=2 carrying a current in SE direction ( diagonally downward); y=4x In a regional magnetic field that is given in vector notation by B = ( y i - x j )/(x^2+y^2+25) As components Bx = (y+1)/x^2+y^2+25) By = (1- x )/(x^2+y^2+25) Find the integral expression for the net force for each branch carrying 5 ampere current.arrow_forward
- An electric power station that operates at 30 KV and uses a 15:1 set step-up ideal transformer is producing 400MW (Mega-Watt) of power that is to be sent to a big city with only 2.0% loss. What which is located 270 km away is the resistance of the Two wires that are being used? 52arrow_forwardSlink, from Toy Story, is a slinky dog whose middle section is a giant spring with a spring constant of 10.9 N/m. Woody, who has a mass of 0.412 kg, grabs onto the tail end of Slink and steps off the bed (as shown in figure A) with no initial velocity and reaches the floor right as his velocity hits zero again (as shown in figure C).arrow_forwardThe character Min Min from Arms was a DLC character added to Super Smash Bros. Min Min’s arms are large springs, with a spring constant of 8.53 ⋅ 10^3 N/m, which she uses to punch and fling away her opponents. Min Min pushes her spring arm against Steve, who is not moving, compressing it 1.20 m as shown in figure A. Steve has a mass of 81.6 kg. Assuming she uses only the spring to launch Steve, how fast is Steve moving when the spring is no longer compressed? As Steve goes flying away he goes over the edge of the level, as shown in figure C. What is the magnitude of Steve’s velocity when he is 2.00 m below where he started?arrow_forward
- Calculate the energy needed to melt 50 g of 0°C icearrow_forwardTwo very long line charges are set up along lines that areparallel to the z-axis, so they set up Electric fields strictly in the xy plane. One goes throughthe x-axis at x = −0.40 m and has charge a density λ1 = +12.0 μC/m, the other goesthrough the x-axis at x = +0.40 m has charge density λ2 = −8.0 μC/m.A. Find the Electric field at point A: (0.40, 0.80) (distances in meters). Give answersin unit vector notation and draw a graph of the x-y plane with the E-fields you justfound.B. Find a point on the x-axis at which the total E-field is 0.arrow_forwardIn order to increase the amount of exercise in her daily routine, Tara decides to walk up the four flights of stairs to her car instead of taking the elevator. Each of the steps she takes are 18.0 cm high, and there are 12 steps per flight. (a) If Tara has a mass of 77.0 kg, what is the change in the gravitational potential energy of the Tara-Earth system (in J) when she reaches her car? ] (b) If the human body burns 1.5 Calories (6.28 x 10³ J) for each ten steps climbed, how much energy (in J) has Tara burned during her climb? ] (c) How does the energy she burned compare to the change in the gravitational potential energy of the system? Eburned Δυarrow_forward
- A 4.40 kg steel ball is dropped onto a copper plate from a height of 10.0 m. If the ball leaves a dent 2.75 mm deep, what is the average force exerted by the plate on the ball during the impact? Narrow_forwardA block of mass m = 7.00 kg is released from rest from point and slides on the frictionless track shown in the figure below. (Assume h₂ = 7.80 m.) a m ha 3.20 m 2.00 m i (a) Determine the block's speed at points ® and point B ©. m/s m/s point (b) Determine the net work done by the gravitational force on the block as it moves from point J A to pointarrow_forwardA 1.10 x 10²-g particle is released from rest at point A on the inside of a smooth hemispherical bowl of radius R R B 2R/3 (a) Calculate its gravitational potential energy at A relative to B. ] (b) Calculate its kinetic energy at B. ] (c) Calculate its speed at B. m/s (d) Calculate its potential energy at C relative to B. J (e) Calculate its kinetic energy at C. ] = 26.5 cm (figure below).arrow_forward
 College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill AstronomyPhysicsISBN:9781938168284Author:Andrew Fraknoi; David Morrison; Sidney C. WolffPublisher:OpenStax
AstronomyPhysicsISBN:9781938168284Author:Andrew Fraknoi; David Morrison; Sidney C. WolffPublisher:OpenStax





