The mass moment of inertia of the machine component with respect to the axis through the origin characterized by the unit vector ( − 3 i − 6 j + 2 k ) / 7 .

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter B, Problem B.61P

To determine

The mass moment of inertia of the machine component with respect to the axis through the origin characterized by the unit vector (−3i−6j+2k)/7.

Expert Solution & Answer

Answer to Problem B.61P

The mass moment of inertia of the machine component with respect to the axis through the origin by the unit vector is 42.75×10−3 lb⋅ft⋅s2.

Explanation of Solution

Given information:

The diameter of the formed steel wire is 18 in, unit vector is (−3i−6j+2k)/7 and the specific weight of the steel is 490 lb/ft3.

The below figure represents the schematic diagram of the wire.

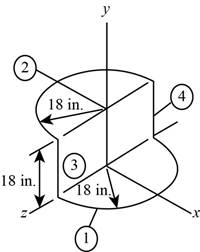
Vector Mechanics For Engineers, Chapter B, Problem B.61P

Figure-(1)

Concept used:

Expression of mass of the steel wire.

m=ρSTV ........ (I)

Here, density of the steel wire is ρST and the volume of the steel wire is V.

Expression of density of the steel wire.

ρST=γSTg ........ (II)

Here, the specific weight of the steel wire is γST and the acceleration due to gravity is g.

Substitute γSTg for ρST in Equation (I).

m=(γSTg)V ........ (III)

For section (1).

Substitute m1 for m and V1 for V in Equation (III).

m1=(γSTg)V1 ........ (IV)

Expression of volume of the steel wire after formation for section (1).

V1=(π4d12)(πd) ........ (V)

Here, the diameter of the formed wire is d1 and the diameter of the wire is d.

For section (2).

Substitute m2 for m and V2 for V in Equation (III).

m2=(γSTg)V2 ........ (VI)

Expression of volume of the steel wire after formation for section (2).

V2=(π4d12)(πd) ........ (VII)

For section (3).

Substitute m3 for m and V3 for V in Equation (III).

m3=(γSTg)V3 ........ (VIII)

Expression of volume of the steel wire after formation for section (3).

V3=(π4d12)(d) ........ (IX)

For section (4).

Substitute m4 for m and V4 for V in Equation (III).

m4=(γSTg)V4 ........ (X)

Expression of volume of the steel wire after formation for section (4).

V4=(π4d12)(d) ........ (XI)

Expression of Moment of inertia about x axis of the wire.

Ix=(Ix)1+(Ix)2+(Ix)3+(Ix)4 ........ (XII)

Here, the moment of inertia of section (1) about the x axis is (Ix)1, the moment of inertia of section (2) about the x axis is (Ix)2, the moment of inertia of section (3) about the x axis is (Ix)3 and the moment of inertia of section (4) about the x axis is (Ix)4.

Expression of moment of inertia of section (1) about the x axis.

(Ix)1=12m1d2 ........ (XIII)

Expression of moment of inertia of section (2) about the x axis.

(Ix)2=12m2d2+m2d2 ........ (XIV)

Expression of moment of inertia of section (3) about the x axis.

(Ix)3=112m3d2+m3{(d2)2+d2} ........ (XV)

Expression of moment of inertia of section (4) about the x axis.

(Ix)4=112m4d2+m4{(d2)2+d2} ........ (XVI)

Expression of Moment of inertia about y axis of the wire.

Iy=(Iy)1+(Iy)2+(Iy)3+(Iy)4 ........ (XVII)

Here, the moment of inertia of section (1) about the y axis is (Iy)1, the moment of inertia of section (2) about the y axis is (Iy)2, the moment of inertia of section (3) about the y axis is (Iy)3 and the moment of inertia of section (4) about the y axis is (Iy)4.

Expression of moment of inertia of section (1) about the y axis.

(Iy)1=m1d2 ........ (XVIII)

Expression of moment of inertia of section (2) about the y axis.

(Iy)2=m2d2 ........ (XIX)

Expression of moment of inertia of section (3) about the y axis.

(Iy)3=m3d2 ........ (XX)

Expression of moment of inertia of section (4) about the y axis.

(Iy)4=m4d2 ........ (XXI)

Expression of Moment of inertia about z axis of the wire.

Iz=(Iz)1+(Iz)2+(Iz)3+(Iz)4 ........ (XXII)

Here, the moment of inertia of section (1) about the z axis is (Iz)1, the moment of inertia of section (2) about the z axis is (Iz)2, the moment of inertia of section (3) about the z axis is (Iz)3 and the moment of inertia of section (4) about the z axis is (Iz)4.

Expression of moment of inertia of section (1) about the z axis.

(Iz)1=12m1d2 ........ (XXIII)

Expression of moment of inertia of section (2) about the z axis.

(Iz)2=12m2d2+m2d2 ........ (XXIV)

Expression of moment of inertia of section (3) about the z axis.

(Iz)3=13m3d2 ........ (XXV)

Expression of moment of inertia of section (4) about the z axis.

(Iz)4=13m4d2 ........ (XXVI)

Mass products of inertia Ixy is expressed as follows:

Ixy=∑(Ix′y′+mxy) …… (XXVII)

Here. Mass products of inertia is Ixy.

Mass products of inertia Iyz is expressed as follows:

Iyz=∑(Iyz) …… (XXVIII)

Here. Mass products of inertia is Iyz.

Mass products of inertia Izx is expressed as follows:

Izx=∑(Izx) ……(XXIX)

Here. Mass products of inertia is Izx.

Calculation:

Substitute 18 in for d1 and 18 in for d in Equation (V).

V1=(π4(18 in)2)(π(18 in))=(0.01227 in2)(π(18 in))=(0.694 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=4.016×10−4 ft3

Substitute 4.016×10−4 ft3 for V2, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (IV).

m1=(490 lb/ft332.2 ft/s2)(4.016×10−4 ft3)=(15.217 lb⋅s2/ft4)(4.016×10−4 ft3)=6.1112×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (VII).

V2=(π4(18 in)2)(π(18 in))=(0.01227 in2)(π(18 in))=(0.694 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=4.016×10−4 ft3

Substitute 4.016×10−4 ft3 for V2, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (VI).

m2=(490 lb/ft332.2 ft/s2)(4.016×10−4 ft3)=(15.217 lb⋅s2/ft4)(4.016×10−4 ft3)=6.1112×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (IX).

V3=(π4(18 in)2)(18 in)=(0.01227 in2)(18 in)=(0.22086 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=1.2783×10−4 ft3

Substitute 1.2783×10−4 ft3 for V3, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (VIII).

m3=(490 lb/ft332.2 ft/s2)(1.2783×10−4 ft3)=(15.217 lb⋅s2/ft4)(1.2783×10−4 ft3)=1.945×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (XI).

V4=(π4(18 in)2)(18 in)=(0.01227 in2)(18 in)=(0.22086 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=1.2783×10−4 ft3

Substitute 1.2783×10−4 ft3 for V4, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (X).

m4=(490 lb/ft332.2 ft/s2)(1.2783×10−4 ft3)=(15.217 lb⋅s2/ft4)(1.2783×10−4 ft3)=1.945×10−3 lb⋅s2/ft

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XIII).

(Ix)1=12(6.1112×10−3 lb⋅s2/ft)(18 in)2=12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=12(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=6.8751×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XIV).

(Ix)2=12(6.1112×10−3 lb⋅s2/ft)(18 in)2+(6.1112×10−3 lb⋅s2/ft)(18 in)2=[12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2]=(6.8751×10−3 ft⋅s2)+(13.7502×10−3 ft⋅s2)=20.6252×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XV).

(Ix)3=[112(1.945×10−3 lb⋅s2/ft)(18 in)2+(1.945×10−3 lb⋅s2/ft){(18 in2)2+(18 in)2}]=[112(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(1.945×10−3 lb⋅s2/ft)[{(18 in2)(1 ft12 in)}2+{(18 in)(1 ft12 in)}2]]=(0.3647×10−3 lb⋅ft⋅s2)+(5.4712×10−3 lb⋅ft⋅s2)=5.8359×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XVI).

(Ix)4=[112(1.945×10−3 lb⋅s2/ft)(18 in)2+(1.945×10−3 lb⋅s2/ft){(18 in2)2+(18 in)2}]=[112(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(1.945×10−3 lb⋅s2/ft)[{(18 in2)(1 ft12 in)}2+{(18 in)(1 ft12 in)}2]]=(0.3647×10−3 lb⋅ft⋅s2)+(5.4712×10−3 lb⋅ft⋅s2)=5.8359×10−3 lb⋅ft⋅s2

Substitute 6.8751×10−3 lb⋅ft⋅s2 for (Ix)1, 20.6252×10−3 lb⋅ft⋅s2 for (Ix)2, 5.8359×10−3 lb⋅ft⋅s2 for (Ix)3 and 5.8359×10−3 lb⋅ft⋅s2 for (Ix)4 in Equation (XII).

Ix=[(6.8751×10−3 lb⋅ft⋅s2)+(20.6252×10−3 lb⋅ft⋅s2)+(5.8359×10−3 lb⋅ft⋅s2)+(5.8359×10−3 lb⋅ft⋅s2)]=(27.5003×10−3 lb⋅ft⋅s2)+(11.6718×10−3 lb⋅ft⋅s2)=39.1721×10−3 lb⋅ft⋅s2

Thus, the mass moment of inertia of the wire with respect to x axis is 39.1721×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XVIII).

(Iy)1=(6.1112×10−3 lb⋅s2/ft)(18 in)2=(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=13.7502×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XIX).

(Iy)2=(6.1112×10−3 lb⋅s2/ft)(18 in)2=(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=13.7502×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XX).

(Iy)3=(1.945×10−3 lb⋅s2/ft)(18 in)2=(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=4.3769×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XXI).

(Iy)4=(1.945×10−3 lb⋅s2/ft)(18 in)2=(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=4.3769×10−3 lb⋅ft⋅s2

Substitute 13.7502×10−3 lb⋅ft⋅s2 for (Iy)1, 13.7502×10−3 lb⋅ft⋅s2 for (Iy)2, 4.3769×10−3 lb⋅ft⋅s2 for (Ix)3 and 4.3769×10−3 lb⋅ft⋅s2 for (Ix)4 in Equation (XVII).

Iy=[(13.7502×10−3 lb⋅ft⋅s2)+(13.7502×10−3 lb⋅ft⋅s2)+(4.3769×10−3 lb⋅ft⋅s2)+(4.3769×10−3 lb⋅ft⋅s2)]=(27.5004×10−3 lb⋅ft⋅s2)+(8.7538×10−3 lb⋅ft⋅s2)=36.2542×10−3 lb⋅ft⋅s2

Thus, the mass moment of inertia of the wire with respect to y axis is 36.2542×10−3 lb⋅ft⋅s2.

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XXIII).

(Iz)1=12(6.1112×10−3 lb⋅s2/ft)(18 in)2=12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=12(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=6.8751×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XXIV).

(Iz)2=12(6.1112×10−3 lb⋅s2/ft)(18 in)2+(6.1112×10−3 lb⋅s2/ft)(18 in)2=[12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2]=(6.8751×10−3 ft⋅s2)+(13.7502×10−3 ft⋅s2)=20.6252×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XXV).

(Iz)3=13(1.945×10−3 lb⋅s2/ft)(18 in)2=13(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=1.4590×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XXVI).

(Iz)4=13(1.945×10−3 lb⋅s2/ft)(18 in)2=13(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=1.4590×10−3 lb⋅ft⋅s2

Substitute 6.8751×10−3 lb⋅ft⋅s2 for (Iz)1, 20.6252×10−3 lb⋅ft⋅s2 for (Iz)2, 1.4590×10−3 lb⋅ft⋅s2 for (Iz)3 and 1.4590×10−3 lb⋅ft⋅s2 for (Iz)4 in Equation (XXII).

Iz=[(6.8751×10−3 lb⋅ft⋅s2)+(20.6252×10−3 lb⋅ft⋅s2)+(1.4590×10−3 lb⋅ft⋅s2)+(1.4590×10−3 lb⋅ft⋅s2)]=(27.5003×10−3 lb⋅ft⋅s2)+(3.098×10−3 lb⋅ft⋅s2)=30.5983×10−3 lb⋅ft⋅s2

Product of inertia (Ix′y′)1,(Ix′y′)2,(Ix′y′)3,(Ix′y′)4,(Iy′z′)1,(Iy′z′)2,(Iz′x′)3,(Iz′x′)4,y1,y2,x3 and x4 are zero due to symmetry.

Substitute 0 for all product of inertia (Ix′y′) in equation (XXVII).

Ixy=∑(0+mxy)Ixy=m2x2y2Ixy=(6.1112×10−3)×(−2×18π×12)(1812)Ixy=−8.7536×10−3 lb⋅ft⋅s2

Substitute (m3y3z3)+(m4y4z4) for product of inertia ∑(Iyz) in equation (XXVIII).

Iyz=(m3y3z3)+(m4y4z4)Iyz=((1.945×10−3)×y3z3)+((1.945×10−3)y3(−z3)) (Y3=Y4z4=−z3)Iyz=0

Substitute 0 for product of inertia ∑(Izx) in equation (XXIX).

Izx=0

Mass moment of inertia of the machine component with respect to the axis through the origin by the unit vector is calculated as follows:

I=Ixλx2+Iyλy2+Izλz2−2Ixyλxλy−2Iyzλzλy−2IzxλzλxI=[(39.1721×10−3)(−37)2+(36.2542×10−3)(−67)2+(30.5983×10−3)(27)2−2×(−8.7536×10−3)(−37)(−67)−0−0]×10−3I=(7.1948+26.6357+2.4978+6.4312)×10−3I=42.75×10−3 lb⋅ft⋅s2

Conclusion:

The mass moment of inertia of the machine component with respect to the axis through the origin by the unit vector is 42.75×10−3 lb⋅ft⋅s2.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

##### For the attached electropneumatic circuit, design where and how a counter should be attached so that a part is counted for each cycle

If you have a spring mass damper system, given by m*x_double_dot + c*x_dot + kx = 0 where m, c, k (all positive scalars) are the mass, damper coefficient, and spring coefficient, respectively. x ∈ R represents the displacement of the mass. Let us then discuss the stability of the system by using Lyapunov stability theorem. Consider the system energy as a candidate Lyapunov function shown in the image. Discuss the positive definiteness of V (x, x_dot). Derive the Lyapunov rate of this system (i.e., V_dot ), and discuss the stability property of thesystem based on the information we gain from ̇V_dot .

In class, two approaches—Theorems 1 and 2 below—are discussed to prove asymptotic stability of asystem when ̇V = 0. Show the asymptotic stability of the system given in Eq. (1) by applying Theorem 1. Show the asymptotic stability of the system given in Eq. (1) by applying Theorem 2.

Answer 2