
Concept explainers
(a)
Find the principal moment of inertia at the origin O.
(a)
Answer to Problem 9.179P
The principal moment of inertia at the origin O is
Explanation of Solution
Given information:
The mass of the cylinder is denoted by m.
The length of the circular cylinder is denoted by a.
The diameter OB of the top surface makes
Calculation:
Show the homogeneous circular cylinder as shown in Figure 1.
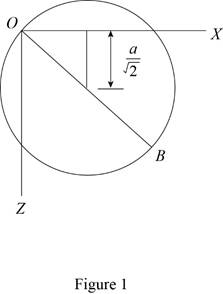
Refer Figure 1.
Refer Figure 9.28.
Apply parallel axis theorem
Show the moment of inertia of the circular cylinder about the y axis as follows:
Show the moment of inertia of the circular cylinder about the x and z axis as follows:
Here, a is the radius of the cylinder and L is the length of the cylinder.
Substitute
The centroidal axis products of inertia are zero due to symmetry.
Write the centroidal locations as measured from the origin O along the x, y and z axis as below;
Express the moment of inertia
Express the moment of inertia
Express the moment of inertia
Show the Equation 9.56 as follows:
Substitute
Substitute
Solve the above Equation and get the values of
Show the principal moment of inertia as follows:
Thus, the principal mass moment of inertia are
(b)
Find the angles made by the principal axis of inertia at O with the coordinate axis.
(b)
Answer to Problem 9.179P
The angles made by the principal axis of inertia at O with the coordinate axis is
Explanation of Solution
Given information:
Consider the direction cosines of each principal axis are denoted by
Calculation:
Refer Part (a).
Show the Equation 9.54 as follows:
Substitute
Modify Equation (3).
Consider
Solve Equation (4).
Add both the Equation in Equation (4).
Substitute
Show the Equation 9.57 as follows:
Substitute
Consider K1.
Substitute
Calculate the value of
Substitute
Show the direction cosines
Conisder K3.
Substitute
Calculate the value of
Substitute
Show the direction cosines
Consider K2.
Show the Equation 9.54b as follows:
Substitute
Refer Equation (3) and (6).
Substitute
Modify above Equations as follows:
Solve Equation (8) and get the value of
Show the Equation 9.57 as follows:
Substitute
Show the direction cosines
Thus, the velocity of the point B is
(c)
Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis.
(c)
Explanation of Solution
Given information:
Calculation:
Refer Part (a) and (b).
Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis as shown in Figure 2.
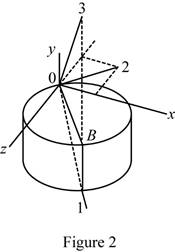
Refer Figure 2.
The principal axis 1 and 3 lies on the vertical plane of symmetry passing through OB.
The principal axis 2 lies in xz plane.
Want to see more full solutions like this?
Chapter 9 Solutions
VECTOR MECH....F/ENGNRS-STATICS -CONNECT
- The moment of inertia of the plane region about the x-axis and the centroidal x-axis are Ix=0.35ft4 and Ix=0.08in.4, respectively. Determine the coordinate y of the centroid and the moment of inertia of the region about the u-axis.arrow_forwardDetermine the product of inertia with respect to the x- and y-axes for the quarter circular, thin ring (tR) by integration.arrow_forward2. A rectangular prism (brick) has dimensions a (in x) b (in y) and c (in z) directions. Taking the origin at the center determine the mass moment of inertia about the y axis in terms of total mass m.arrow_forward
- A/23 The plane figure is symmetrical with respect to the 45° line and has an area of 1600 mm². Its polar mo- ment of inertia about its centroid C is 40(104) mm¹. Compute (a) the polar radius of gyration about O and (b) the radius of gyration about the xo-axis. Ans. (a) ko = 45.3 mm, (b) kxo = 11.18 mm 30 mm 30 mm 45° CHarrow_forwardConsider Figure Q3, Determine the mass moment of inertia of the composite body about the x and y axes. Mass of rod = 2 kg/m Mass of disc = 15 kg/m2arrow_forwardQuestion 4 Calculate the moments of inertia I, and I, of the composite region consisting of the rectangular tri- angle (T) and the wedge (W) with radius r. The wedge is centered symmetrically about the y-axis and spans an angle of 30°. Express your answer in terms of r. Warrow_forward
- For the body shown. If point P3 is the center of mass for rod part P1-P2, and point P4 is the center of mass for rod part P3-P5, and P6 is the center of mass of the disk part. Find the mass moment of inertia around axis perpendicular to the page and passes through point P5. Given; L = 1 m, mass density of rod parts = 5 kg / m, mass density of disk = 12 Kg / m?arrow_forwardFor the figure below answer the following: 1.What best approximates the mass moment of inertia of the composite body about the y-axis? 2. What best approximates the radius of gyration of the composite body about the y-axis?arrow_forwardConsider a wheel of radius r = 0.28 m, with six spokes (or three rods of length equal to the diameter of the wheel). The total mass of the wheel is 3.0 kg and 55% of the mass is evenly distributed on the circumference while the rest is evenly distributed on the spokes. Calculate the moment of inertia. rarrow_forward
- 2. The brick shown below is formed by a rectangular prism with three cylindrical holes. The brick has a density of 2000 kg/m³ and a depth (not pictured) of 50 mm. Each cylindrical hole has a diameter of 50 mm. a. Calculate the total mass of the brick. b. Calculate the center of mass of the brick measured from Point O. You may do this by inspection (no work required). Calculate the moment of inertia of the body about an axis into the plane of the page and passing through Point O. C. y O each dim. 50 mm OOO 200 mm 100 mmarrow_forwardA rigid body is rotating around O in the vertical plane. It consists of two slender rods, each of mass m and length L. At the instant shown, the rigid body has angular velocity w and angular acceleration a. Determine the following: L 0 8 Motion L ,لياarrow_forwardCalculate the mass moment of inertia for a rectangular plate for the H-H axis shown in the link. The mass of the plate is 8 kg, a = 5 m and b = 1 m.arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
