
Concept explainers
9.135 and 9.136 A 2-mm thick piece of sheet steel is cut and bent into the machine component shown. Knowing that the density of steel is 7850 kg/m3, determine the mass moment of inertia of the component with respect to each of the coordinate axes.
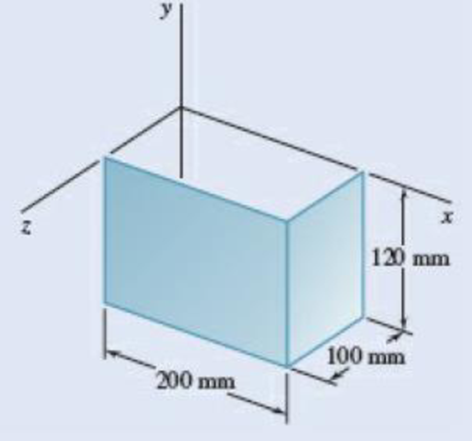
Fig. P9.135
Find the mass moment of inertia of the component with respect to
Answer to Problem 9.135P
The mass moment of inertia of the component with respect to
The mass moment of inertia of the component with respect to
The mass moment of inertia of the component with respect to
Explanation of Solution
Given information:
The thickness (t) of sheet steel is
The density
Calculation:
Sketch the sheet steel as shown in Figure 1.
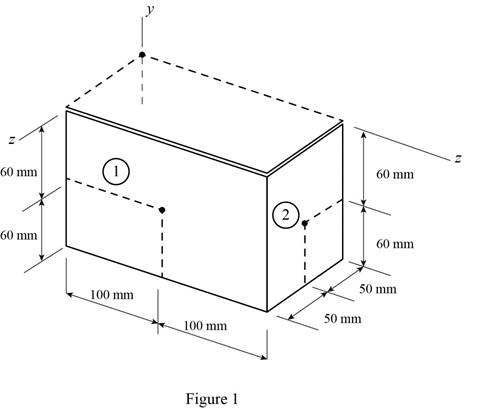
Find the mass of rectangular section 1 as shown in below:
Here,
Express the volume of rectangular section 1 as follows:
Substitute
Find the mass of rectangular section 2 as shown in below:
Here,
Express the volume of rectangular section 2 as follows:
Substitute
Panel 1:
Find the moment of inertia about x axis for panel 1 as shown below:
Substitute
Find the moment of inertia about y axis for panel 1 as shown below:
Substitute
Find the moment of inertia about z axis for panel 1 as shown below:
Substitute
Panel 2:
Find the moment of inertia about x axis for panel 2 as shown below:
Substitute
Find the moment of inertia about y axis for panel 2 as shown below:
Substitute
Find the moment of inertia about z axis for panel 2 as shown below:
Substitute
Find the total mass of inertia
Here,
Substitute
Thus, the mass moment of inertia of the component with respect to
Find the total mass of inertia
Here,
Substitute
Thus, the mass moment of inertia of the component with respect to
Find the total mass of inertia
Here,
Substitute
Thus, the mass moment of inertia of the component with respect to
Want to see more full solutions like this?
Chapter 9 Solutions
VECTOR MECH....F/ENGNRS-STATICS -CONNECT
- B.33 Determine the mass moment of inertia of the steel machine element shown with respect to the axis. (The density of steel is 7850 kg/m³.) 50 mm 50 i 240 min 360 nim 100 mm Fig. PB.32 and PB.33 200 mmarrow_forwardA 4 mm thick piece of sheet steel is cut and bent into the machine component shown. Knowing that the density of steel is 7850 kg/m³, determine the mass moment of inertia of the component with respect to each of the coordinate axes. 100 mm 100 mm 100 mm 80 mm 80 mm 100 mm The mass moment of inertia x is [10282.45 × 10-3 kg.m². The mass moment of inertia ly is [15071.93 × 10−³ kg.m². The mass moment of inertia / is [6933.124 × 10-³ kg-m².arrow_forwardA section of sheet steel 2 mm thick is cut and bent into the machine component shown. Knowing that the density of steel is 7850 kg/m3 , determine the mass products of inertia Ixy, Iyz, and Izx of the component.arrow_forward
- Problem 09.086 - Orientation of the principal axes and the corresponding moments of inertia For the area indicated, determine the orientation of the principal axes at the origin and the corresponding values of the moments of inertia when b= 76 mm and h = 56 mm. b The value of mis The value of 0m2 is The value of Imax is The value of I min is 180 270 1.429 7292 × h x 106 mm4. 106 mm4arrow_forwardFig. PB.15 B.15 A thin steel wire is bent into the shape shown. Dennting the mass per unit length of the wire by m', determine by direct integration the mo- ment of inertia of the wire with respect to each of the coordinate aves. y=(23_123)32arrow_forwardPlease help me answer the following, thanks.arrow_forward
- Two steel plates are welded to a rolled W section as indicated. Knowing that the centroidal moments of inertia Ix and Iy of the combined section are equal, determine (a) the distance a, (b) the moments of inertia with respect to the centroidal x and y axes.arrow_forwardFor items 4 and 5. A thin rectangular plate is welded on the center of the top of a circular cylinder. The mass of the cylinder is 5kg and the mass of the triangular plate is 2kg. Note that the x-axis is located on the centroidal x-axis of the triangular plate. 30cm 26cm 0.1725 m diam. d=7cm X 10cm 4. Which of the following is closest to the moment of inertia of the composite object about the x- axis? 0.208 kg-m^2 5. Which of the following is closest to the radius of gyration of the composite object about the x- axis?arrow_forwardUsing the polar moment of inertia of the isosceles triangle of Prob. 9.28, show that the centroidal polar moment of inertia of a circular area of radius r is π4/2. ( Hint: As a circular area is divided into an increasing number of equal circular sectors, what is the approximate shape of each circular sector?)(Reference to Problem 9.28):Determine the polar moment of inertia and the polar radius of gyration of the isosceles triangle shown with respect to point O.arrow_forward
- B.20 A portion of an 8-in.-long steel rod of diameter 1.50 in. is turned to form the conical section shown. Knowing that the turning process reduces the moment of inertia of the rod with respect to the x axis by 20 percent, de- termine the height h of the cone. Fig. PB.20arrow_forward1.3 cm 1.0 cm -0.5 cm 3.8 cm 0.5 cm AI B 3.6 cm PROBLEM 9.44 Determine the moments of inertia I, and I, of the area shown with respect to centroidal axes respectively parallel and perpendicular to side AB.arrow_forward60 mm 20 mm 10 mm 20 mm 60 mm 10 mm 100 mm- 10 mm- PROBLEM 9.71 Using the parallel-axis theorem, determine the moment of inertia of the area shown with respect to the x-x and y-yaxes.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





