Chapter 9.2, Problem 9.48P

(a)

To determine

Find the polar moment of inertia of the area with respect to point O.

Answer to Problem 9.48P

The polar moment of inertia of the area with respect to point O is $\underset{\_}{12.16\times {10}^6{\text{mm}}^{\text{4}}}$.

Explanation of Solution

Calculation:

Sketch the cross section as shown in Figure 1.

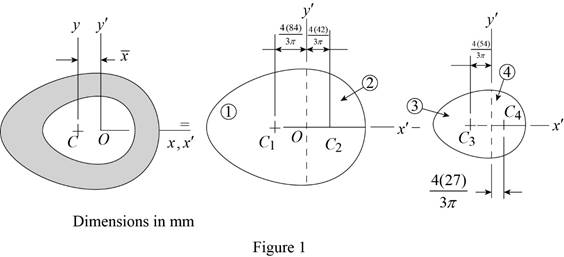
Refer to Figure1.

It is divided into 4 parts as shown above.

Find the area of section 1 ellipsoid using the relation:

$A_1=\frac{\pi }{2}\left(ar\right)$ (1)

Substitute $84\text{mm}$ for a and $42\text{mm}$ for r in Equation (1).

$\begin{array}{c}{A}_1=\frac{\pi }{2}\left(84\right)\left(42\right)\\ =5,541.76{\text{mm}}^{\text{2}}\end{array}$

Find the area of section 2 ellipsoid using the relation:

$A_2=\frac{\pi }{2}{\left(r_o\right)}^2$ (2)

Here, $r_o$ is radius of outer section.

Substitute $42\text{mm}$ for r in Equation (2).

$\begin{array}{c}{A}_2=\frac{\pi }{2}{\left(42\right)}^2\\ =2,770.88{\text{mm}}^{\text{2}}\end{array}$

Find the area of section 3 ellipsoid using the relation:

$A_3=-\frac{\pi }{2}\left(ar\right)$ (3)

Substitute $54\text{mm}$ for a and $\text{27}\text{mm}$ for r in Equation (3).

$\begin{array}{c}{A}_3=-\frac{\pi }{2}\left(54\right)\left(27\right)\\ =-2,290.22{\text{mm}}^{\text{2}}\end{array}$

Find the area of section 4 ellipsoid using the relation:

$A_4=-\frac{\pi }{2}{\left(r_i\right)}^2$ (4)

Substitute $27\text{mm}$ for r in Equation (4).

$\begin{array}{c}{A}_4=-\frac{\pi }{2}{\left(27\right)}^2\\ =-1,145.11{\text{mm}}^{\text{2}}\end{array}$

Find the total are of section (A) as shown below:

$A=A_1+A_2+A_3+A_4$ (5)

Substitute $5,541.76{\text{mm}}^{\text{2}}$ for $A_1$, $2,770.88{\text{mm}}^{\text{2}}$ for $A_2$, $-2,290.22{\text{mm}}^{\text{2}}$ for $A_3$, and $-1,145.11{\text{mm}}^{\text{2}}$ for $A_4$ in Equation (5).

$\begin{array}{c}A=5,541.76+2,770.88-2,290.22-1,145.11\\ =4,877.32{\text{mm}}^{\text{2}}\end{array}$

Find the centroid $\left(x_1\right)$ section 1 as shown below:

$\begin{array}{c}{x}_1=-\frac{112}{\pi }\\ =-35.6507\text{mm}\end{array}$

Find the centroid $\left(x_2\right)$ section 2 as shown below:

$\begin{array}{c}{x}_2=\frac{56}{\pi }\\ =17.8254\text{mm}\end{array}$

Find the centroid $\left(x_3\right)$ section 3 as shown below:

$\begin{array}{c}{x}_3=-\frac{72}{\pi }\\ =-22.9183\text{mm}\end{array}$

Find the centroid $\left(x_4\right)$ section 4 as shown below:

$\begin{array}{c}{x}_4=\frac{36}{\pi }\\ =11.4592\text{mm}\end{array}$

Find the centroid $\left(\overline{x}\right)$ using the relation as follows:

$\overline{x}=\frac{A_1{x}_1+A_2{x}_2+A_3{x}_3+A_4{x}_4}{A_1+A_2+A_3+A_4}$ (6)

Substitute $5,541.76{\text{mm}}^{\text{2}}$ for $A_1$, $2,770.88{\text{mm}}^{\text{2}}$ for $A_2$, $-2,290.22{\text{mm}}^{\text{2}}$ for $A_3$, $-1,145.11{\text{mm}}^{\text{2}}$ for $A_4$, $-35.6507\text{mm}$ for $x_1$, and $17.8254\text{mm}$ for $x_2$, $-22.9183\text{mm}$ for  $x_3$, $11.4592\text{mm}$ for $x_4$ , in Equation (6).

$\begin{array}{c}\overline{x}=\frac{5,541.76\left(-35.6507\right)+2,770.88\left(17.8254\right)-2,290.22\left(-22.9183\right)-1,145.11\left(11.4592\right)}{5,541.76+2,770.88-2,290.22-1,145.11}\\ =\frac{-197,567.62+49,392.044+52,487.949-13,122.0}{4,877.32}\\ =-22.3094\text{mm}\end{array}$

Find the polar moment of inertia ${\left(J_O\right)}_1$ section 1 as shown below:

${\left(J_O\right)}_1=\frac{\pi }{8}\left(a{r}_o\right)\left[a^2+r_o^2\right]$ (7)

Substitute $84\text{mm}$ for a and $42\text{mm}$ for $r_o$ in Equation (7).

$\begin{array}{c}{\left(J_O\right)}_1=\frac{\pi }{8}\left(84\times 42\right)\left[{84}^2+{42}^2\right]\\ =\frac{\pi }{8}\left(84\times 42\right)8,820\\ =12,219,601.62\\ =12.21960\times {10}^6{\text{mm}}^{\text{4}}\end{array}$

Find the polar moment of inertia ${\left(J_O\right)}_2$ section 2 as shown below:

${\left(J_O\right)}_2=\frac{\pi }{4}{r}_o^2$ (8)

Substitute $42\text{mm}$ for $r_o$ in Equation (8).

$\begin{array}{c}{\left(J_O\right)}_2=\frac{\pi }{4}{\left(42\right)}^2\\ =2.444392\times {10}^6{\text{mm}}^{\text{4}}\end{array}$

Find the polar moment of inertia ${\left(J_O\right)}_3$ section 3 as shown below:

${\left(J_O\right)}_3=\frac{\pi }{8}\left(a{r}_i\right)\left[a^2+r_i^2\right]$ (9)

Substitute $54\text{mm}$ for a and $27\text{mm}$ for $r_i$ in Equation (9).

$\begin{array}{c}{\left(J_O\right)}_3=\frac{\pi }{8}\left(54\times 27\right)\left[{54}^2+{27}^2\right]\\ =572.555\left[3,645\right]\\ =2.08696\times {10}^6{\text{mm}}^{\text{4}}\end{array}$

Find the polar moment of inertia ${\left(J_O\right)}_2$ section 2 as shown below:

${\left(J_O\right)}_4=\frac{\pi }{4}{r}_i^2$ (10)

Substitute $27\text{mm}$ for $r_i$ in Equation (10).

$\begin{array}{c}{\left(J_O\right)}_4=\frac{\pi }{4}{\left(27\right)}^2\\ =0.41739\times {10}^6{\text{mm}}^{\text{4}}\end{array}$

Find the total moment of inertia $\left(J_O\right)$ using the relation:

$\left(J_O\right)={\left(J_O\right)}_1+{\left(J_O\right)}_2-{\left(J_O\right)}_3-{\left(J_O\right)}_4$ (11)

Substitute $12.21960\times {10}^6{\text{mm}}^{\text{4}}$ for ${\left(J_O\right)}_1$, $2.444392\times {10}^6{\text{mm}}^{\text{4}}$ for ${\left(J_O\right)}_2$, $2.08696\times {10}^6{\text{mm}}^{\text{4}}$ for ${\left(J_O\right)}_3$, and $0.41739\times {10}^6{\text{mm}}^{\text{4}}$ for ${\left(J_O\right)}_4$ in Equation (11).

$\begin{array}{c}\left(J_O\right)=12.21960\times {10}^6+2.444392\times {10}^6-2.08696\times {10}^6-0.41739\times {10}^6\\ =12,159,652\\ =12.16\times {10}^6{\text{mm}}^{\text{4}}\end{array}$

Thus, the polar moment of inertia of the area with respect to point O is $\underset{\_}{12.16\times {10}^6{\text{mm}}^{\text{4}}}$.

(b)

To determine

Find the centroid of area.

Answer to Problem 9.48P

The centroid of area is $\underset{\_}{9.73\times {10}^6{\text{mm}}^{\text{4}}}$.

Explanation of Solution

Calculation:

Find the centroid of area using the relation:

$J_O=J_C+A{\overline{X}}^2$ (12)

Substitute $12.16\times {10}^6{\text{mm}}^{\text{4}}$ for $J_O$, $4,877.32{\text{mm}}^{\text{2}}$ for A, and $-22.3094\text{mm}$ for $\overline{x}$,and $0.7468\text{in}$ for $\overline{y}$ in Equation (12).

$\begin{array}{l}12.16\times {10}^6=J_C+\left(4,877.32\right){\left(-22.3094\right)}^2\\ 12.16\times {10}^6=J_C+2,427,487.66\\ J_C=9.73\times {10}^6{\text{mm}}^{\text{4}}\end{array}$

Thus, the centroid of area is $\underset{\_}{9.73\times {10}^6{\text{mm}}^{\text{4}}}$.