DISCRETE MATHEMATICS LOOSELEAF
8th Edition
ISBN: 9781264309689
Author: ROSEN
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 9.6, Problem 25E
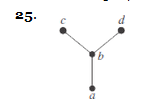
Exercises 25-27 list all ordered pairs in the partial ordering with the accompanying Hasse diagram.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Identify the lower class limits, upper class limits,
class width, class midpoints, and class
boundaries for the given frequency distribution.
Also identify the number of individuals included
in the summary.
Blood Platelet Count of
Males (1000 cells/µL)
0-99
Frequency
2
100-199
46
200-299
95
300-399
11
400-499
0
500-599
1
600-699
0
...
Identify the lower class limits (in 1000 cells/μL).
(Type integers or decimals. Do not round. Use ascending order.)
Identify the upper class limits (in 1000 cells/μL).
(Type integers or decimals. Do not round. Use ascending order.)
Identify the class width (in 1000 cells/µL).
(Type an integer or a decimal. Do not round.)
Identify the class midpoints (in 1000 cells/μL).
------
(Type integers or decimals. Do not round. Use ascending order.)
Identify the class boundaries (in 1000 cells/μL).
(Type integers or decimals. Do not round. Use ascending order.)
Identify the number of individuals included in the summary.
(Type an integer or a decimal. Do not round.)
Find the (a) mean, (b) median, (c) mode, and (d) midrange for the data and then (e) answer the given question.
Listed below are the jersey numbers of 11 players randomly selected from the roster of a championship sports team. What do the results tell us?
71 9 67 48 14 23 65 89 8 10 7吋
a. Find the mean.
The mean is
(Type an integer or a decimal rounded to one decimal place as needed.)
b. Find the median.
The median is
(Type an integer or a decimal rounded to one decimal place as needed.)
c. Find the mode.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
○ A. The mode(s) is (are) ☐.
(Type an integer or a decimal. Do not round. Use a comma to separate answers as needed.)
B. There is no mode.
d. Find the midrange.
The midrange is
(Type an integer or a decimal rounded to one decimal place as needed.)
e. What do the results tell us?
A. The midrange gives the average (or typical) jersey number, while the mean and median give two different…
Fill in the blank.
The complement of "at least one" is
The complement of "at least one" is
"one."
"one or less."
"more than one."
"none."
Chapter 9 Solutions
DISCRETE MATHEMATICS LOOSELEAF
Ch. 9.1 - t the ordered pairs in the...Ch. 9.1 - a) List all the ordered pairs in the relation R =...Ch. 9.1 - each of these relations on the set {1, 2, 3, 4},...Ch. 9.1 - ermine whether the relationRon the set of all...Ch. 9.1 - ermine whether the relationRon the set of all Web...Ch. 9.1 - ermine whether the relationRon the set of all real...Ch. 9.1 - ermine whether the relationRon the set of all...Ch. 9.1 - w that the relationR=Oon a nonempty set S is...Ch. 9.1 - Show that the relationR=on the empty setS=is...Ch. 9.1 - e an example of a relation on a set that is a)...
Ch. 9.1 - Which relations in Exercise 3 are irreflexive?Ch. 9.1 - Which relations in Exercise 4 are irreflexive?Ch. 9.1 - Which relations in Exercise 5 are irreflexive?Ch. 9.1 - Which relations in Exercise 6 are irreflexive?Ch. 9.1 - Can a relation on a set be neither reflexive nor...Ch. 9.1 - Use quantifiers to express what it means for a...Ch. 9.1 - Give an example of an irreflexive relation on the...Ch. 9.1 - Which relations in Exercise 3 are asymmetric?Ch. 9.1 - Which relations in Exercise 4 are asymmetric?Ch. 9.1 - Which relations in Exercise 5 are asymmetric?Ch. 9.1 - Which relations in Exercise 6 are asymmetric?Ch. 9.1 - Must an asymmetric relation also be antisymmetric?...Ch. 9.1 - Use quantifiers to express what it means for...Ch. 9.1 - Give an example of an asymmetric relation on the...Ch. 9.1 - many different relations are there from a set...Ch. 9.1 - Rbe the relationR={(a,b)ab}on the set of integers....Ch. 9.1 - Rbe the relationR={(a,b) |adividesb} on the set of...Ch. 9.1 - Let R be the relation on the set of all states in...Ch. 9.1 - pose that the functionffromAtoBis a one-to-one...Ch. 9.1 - R1= {(1, 2), (2, 3), (3, 4)} andR2= {(1, 1), (1,...Ch. 9.1 - Abe the set of students at your school andBthe set...Ch. 9.1 - Rbe the relation {(1, 2), (1, 3), (2, 3), (2,4),...Ch. 9.1 - 33.LetRbe the relation on the set of people...Ch. 9.1 - rcises 34-38 deal with these relations on the set...Ch. 9.1 - rcises 34-38 deal with these relations on the set...Ch. 9.1 - rcises 34-38 deal with these relations on the set...Ch. 9.1 - rcises 34-38 deal with these relations on the set...Ch. 9.1 - rcises 34-38 deal with these relations on the set...Ch. 9.1 - d the relationsS2fori= 1, 2, 3,4, , 6i’here...Ch. 9.1 - Rbe the parent relation on the set of all people...Ch. 9.1 - Rbe the relation on the set of people with...Ch. 9.1 - R1andR2be the divides” and ‘is a multiple of...Ch. 9.1 - R1andR2be the “congruent modulo 3” and the...Ch. 9.1 - List the 16 different relations on the set {0,1}.Ch. 9.1 - How many of the 16 different relations on {0,1}...Ch. 9.1 - ch of the 16 relations on {o, 1}, which you listed...Ch. 9.1 - a) How many relations are there on the set...Ch. 9.1 - S be a set withnelements and letaandbbe distinct...Ch. 9.1 - How many relations are there on a set...Ch. 9.1 - How many transitive relations are there on a set...Ch. 9.1 - d the error in the “proof” of the following...Ch. 9.1 - pose thatRandSare reflexive relations on a setA....Ch. 9.1 - w that the relationRon a setAis symmetric if and...Ch. 9.1 - w that the relationRon a setAis antisymmetric if...Ch. 9.1 - w that the relationRon a setAis reflexive if and...Ch. 9.1 - w that the relationRon a setAis reflexive if and...Ch. 9.1 - Rbe a relation that is reflexive and transitive....Ch. 9.1 - Rbe the relation on the set {1, 2, 3,4 , 5}...Ch. 9.1 - Rbe a reflexive relation on a setA. Show thatRnis...Ch. 9.1 - Prob. 60ECh. 9.1 - Suppose that the relationRis irreflexive....Ch. 9.1 - ive a big-O estimate for the number of integer...Ch. 9.2 - List the triples in the relation {(a, b, c)|a,...Ch. 9.2 - ch 4-tuples are in the relation {(a,b, c, d)| a,...Ch. 9.2 - Prob. 3ECh. 9.2 - uming that no newn-tuples are added, find all the...Ch. 9.2 - Prob. 5ECh. 9.2 - uming that no new n-tuples are added, find a...Ch. 9.2 - Prob. 7ECh. 9.2 - Prob. 8ECh. 9.2 - 5-tuples in a 5-ary relation represent these...Ch. 9.2 - What do you obtain when you apply the selection...Ch. 9.2 - What do you obtain when you apply the selection...Ch. 9.2 - What do you obtain when you apply the selection...Ch. 9.2 - t do you obtain when you apply the selection...Ch. 9.2 - t do you obtain when you apply the...Ch. 9.2 - Prob. 15ECh. 9.2 - Display the table produced by applying the...Ch. 9.2 - play the table produced by applying the...Ch. 9.2 - many components are there in then-tuples in the...Ch. 9.2 - Construct the table obtained by applying the join...Ch. 9.2 - w that ifC1andC2are conditions that elements of...Ch. 9.2 - w that if C1andC2are conditions that elements...Ch. 9.2 - Prob. 22ECh. 9.2 - Prob. 23ECh. 9.2 - w that ifCis a condition that elements of the nary...Ch. 9.2 - w that ifRandSare bothn-ary relations,...Ch. 9.2 - Give an example to show that ifRandSare bothn-ary...Ch. 9.2 - e an example to show that ifRandSare bothn-ary...Ch. 9.2 - a) What are the operations that correspond to the...Ch. 9.2 - Prob. 29ECh. 9.2 - Prob. 30ECh. 9.2 - ermine whether there is a primary key for the...Ch. 9.2 - Show that ann-aryrelation with a primary key can...Ch. 9.2 - Prob. 33ECh. 9.2 - Prob. 34ECh. 9.2 - Prob. 35ECh. 9.2 - Prob. 36ECh. 9.2 - Prob. 37ECh. 9.2 - Prob. 38ECh. 9.2 - Prob. 39ECh. 9.2 - Show that if an item set is frequent in a set of...Ch. 9.2 - Prob. 41ECh. 9.3 - resent each of these relations on {1, 2, 3} with a...Ch. 9.3 - resent each of these relations on {1, 2,3, 4} with...Ch. 9.3 - List the ordered pairs in the relations on {1, 2,...Ch. 9.3 - t the ordered pairs in the relations on {1,2,3,4)...Ch. 9.3 - can the matrix representing a relationRon a setAbe...Ch. 9.3 - can the matrix representing a relationRon a setAbe...Ch. 9.3 - ermine whether the relations represented by the...Ch. 9.3 - Determine whether the relation represented by the...Ch. 9.3 - many nonzero entries does the matrix representing...Ch. 9.3 - many nonzero entries does the matrix representing...Ch. 9.3 - How can the matrixR, the complement of the...Ch. 9.3 - How can the matrix forR1, the inverse of the...Ch. 9.3 - LetRbe the relation represented by the matrix...Ch. 9.3 - R1andR2be relations on a setArepresented by the...Ch. 9.3 - Rbe the relation represented by the matrix...Ch. 9.3 - Rbe a relation on a set A withnelements. If there...Ch. 9.3 - Rbe a relation on a set A withnelements. If there...Ch. 9.3 - Draw the directed graphs representing each of the...Ch. 9.3 - Draw the directed graphs representing each of the...Ch. 9.3 - Draw the directed graph representing each of the...Ch. 9.3 - Draw the directed graph representing each of the...Ch. 9.3 - Draw the directed graph that represents the...Ch. 9.3 - Exercises 23-28 list the ordered pairs in the...Ch. 9.3 - Exercises 23-28 list the ordered pairs in the...Ch. 9.3 - Prob. 25ECh. 9.3 - Prob. 26ECh. 9.3 - Prob. 27ECh. 9.3 - Exercises 23-28 list the ordered pairs in the...Ch. 9.3 - can the directed graph of a relationRon a finite...Ch. 9.3 - How can the directed graph of a relationRon finite...Ch. 9.3 - ermine whether the relations represented by the...Ch. 9.3 - ermine whether the relations represented by the...Ch. 9.3 - LetRbe a relation on a setA, Explain how to use...Ch. 9.3 - Rbe a relation on a set A. Explain how to use the...Ch. 9.3 - w that ifMRis the matrix representing the...Ch. 9.3 - Prob. 36ECh. 9.4 - Rbe the relation on the set {o, 1, 2, 3}...Ch. 9.4 - LetRbe the relation{(a,b)ab}on the set of...Ch. 9.4 - Rbe the relation{(a,b)| adividesb} on the set of...Ch. 9.4 - How can the directed graph representing the...Ch. 9.4 - Exercises 5-7 draw the directed graph of the...Ch. 9.4 - Exercises 5-7 draw the directed graph of the...Ch. 9.4 - Prob. 7ECh. 9.4 - How can the directed graph representing the...Ch. 9.4 - d the directed graphs of the symmetric closures of...Ch. 9.4 - Find the smallest relation containing the relation...Ch. 9.4 - Prob. 11ECh. 9.4 - Suppose that the relationRon the finite setAis...Ch. 9.4 - Prob. 13ECh. 9.4 - Prob. 14ECh. 9.4 - n is it possible to define the ‘irreflexive...Ch. 9.4 - Prob. 16ECh. 9.4 - Prob. 17ECh. 9.4 - Prob. 18ECh. 9.4 - Rbe the relation on the set{1,2,3,4,5} containing...Ch. 9.4 - Rbe the relation that contains the pair (a,b)...Ch. 9.4 - Rbe the relation on the set of all students...Ch. 9.4 - Suppose that the relationRis reflexive. Show...Ch. 9.4 - Suppose that the relationRis symmetric. Show...Ch. 9.4 - pose that the relationRis irreflexive. Is the...Ch. 9.4 - Algorithm 1 to find the transitive closures of...Ch. 9.4 - Algorithm 1 to find the transitive closures of...Ch. 9.4 - Use Warshall’s algorithm to find the transitive...Ch. 9.4 - Warshall’s algorithm to find the transitive...Ch. 9.4 - d the smallest relation containing the relation...Ch. 9.4 - Finish the proof of the case whenabin Lemma 1.Ch. 9.4 - orithms have been devised that use Q(n2,8) bit...Ch. 9.4 - Devise an algorithm using the concept of interior...Ch. 9.4 - Adapt Algorithm 1 to find the reflexive closure of...Ch. 9.4 - pt Warshall’s algorithm to find the reflexive...Ch. 9.4 - Prob. 35ECh. 9.4 - Prob. 36ECh. 9.5 - Which of these relations on {0, 1, 2,3) are...Ch. 9.5 - ch of these relations on the set of all people are...Ch. 9.5 - ch of these relations on the set of all functions...Ch. 9.5 - ine three equivalence relations on the set of...Ch. 9.5 - Define three equivalence relations on the set of...Ch. 9.5 - ine three equivalence relations on the set of...Ch. 9.5 - Show that the relation of logical equivalence on...Ch. 9.5 - Rbe the relation on the set of all sets of real...Ch. 9.5 - pose thatAis a nonempty set, andfis a function...Ch. 9.5 - pose thatAis a nonempty set andRis an equivalence...Ch. 9.5 - w that the relationRconsisting of all pairs (x, y)...Ch. 9.5 - w that the relationRconsisting of all pairs(x,...Ch. 9.5 - w that the relationRconsisting of all pairs (x, y)...Ch. 9.5 - R be the relation consisting of all pairs (x,y)...Ch. 9.5 - Rbe the relation on the set of ordered pairs of...Ch. 9.5 - Let R be the relation on the set of ordered pairs...Ch. 9.5 - (Requires calculus) a) Show that the relationRon...Ch. 9.5 - Prob. 18ECh. 9.5 - Rbe the relation on the set of all URLs (or Web...Ch. 9.5 - Rbe the relation on the set of all people who have...Ch. 9.5 - Prob. 21ECh. 9.5 - Prob. 22ECh. 9.5 - Exercises 21-23 determine whether the relation...Ch. 9.5 - Determine whether the relations represented by...Ch. 9.5 - w that the relationRon the set of all bit stings...Ch. 9.5 - t are the equivalence classes of the equivalence...Ch. 9.5 - t are the equivalence classes of the equivalence...Ch. 9.5 - t are the equivalence classes of the equivalence...Ch. 9.5 - What is the equivalence class of the bit string...Ch. 9.5 - t are the equivalence classes of these bit strings...Ch. 9.5 - What are the equivalence classes of the bit...Ch. 9.5 - What are the equivalence classes of the bit...Ch. 9.5 - t are the equivalence classes of the bit strings...Ch. 9.5 - t are the equivalence classes of the bit strings...Ch. 9.5 - t is the congruence class [n]5(that is, the...Ch. 9.5 - What is the congruence class [4]mwhenmis a) 2? b)...Ch. 9.5 - Give a description of each of the congruence...Ch. 9.5 - t is the equivalence class of each of these...Ch. 9.5 - a) What is the equivalence class of(1,2)with...Ch. 9.5 - a) What is the equivalence class of (1, 2) with...Ch. 9.5 - ch of these collections of subsets are partitions...Ch. 9.5 - ch of these collections of subsets are partitions...Ch. 9.5 - ch of these collections of subsets are partitions...Ch. 9.5 - ch of these collections of subsets are partitions...Ch. 9.5 - Prob. 45ECh. 9.5 - ch of these are partitions of the set of real...Ch. 9.5 - t the ordered pairs in the equivalence relations...Ch. 9.5 - t the ordered pairs in the equivalence relations...Ch. 9.5 - w that the partition formed from congruence...Ch. 9.5 - w that the paron of the set of people living in...Ch. 9.5 - w that the partition of the set of bit strings of...Ch. 9.5 - Exercises 52 and 53,Rnrefers to the family of...Ch. 9.5 - Exercises 52 and 53,Rnrefers to the family of...Ch. 9.5 - pose thatR1andR2are equivalence relations on a...Ch. 9.5 - d the smallest equivalence relation on the set...Ch. 9.5 - pose thatR1andR2are equivalence relations on the...Ch. 9.5 - sider the equivalence relation fromExample...Ch. 9.5 - Each bead on a bracelet with three beads is either...Ch. 9.5 - Let R be the relation on the set of all colorings...Ch. 9.5 - a) LetRbe the relation on the set of functions...Ch. 9.5 - Determine the number of different equivalence...Ch. 9.5 - Determine the number of different equivalence...Ch. 9.5 - Do we necessarily get an equivalence relation when...Ch. 9.5 - Do we necessarily get an equivalence relation when...Ch. 9.5 - pose we useTheorem 2to form a partitionP froman...Ch. 9.5 - .Suppose we useTheorem 2to form an equivalence...Ch. 9.5 - ise an algorithm to find the smallest equivalence...Ch. 9.5 - p(n)denote the number of different equivalence...Ch. 9.5 - Use Exercise 68 to find the number of different...Ch. 9.6 - ch of these relations on {0,1,2,3) are partial...Ch. 9.6 - ch of these relations on {0,1,2,3} are partial...Ch. 9.6 - Prob. 3ECh. 9.6 - Prob. 4ECh. 9.6 - ch of these are posets? a)(Z,=) b)(Z,) c)(Z,)...Ch. 9.6 - Which of these are posets?a) (R, =)b) (R,<) c)...Ch. 9.6 - Determine whether the relations represented by...Ch. 9.6 - Determine whether the relations represented by...Ch. 9.6 - Exercises9-11determine whether the relation with...Ch. 9.6 - Exercises9-11determine whether the relation with...Ch. 9.6 - Exercises 9-11 determine whether the relation with...Ch. 9.6 - Prob. 12ECh. 9.6 - d the duals of these posets. a)({0,1,2},) b)(Z,)...Ch. 9.6 - ch of these pairs of elements are comparable in...Ch. 9.6 - Prob. 15ECh. 9.6 - Let S = {1,2,3,4). With respect to the...Ch. 9.6 - d the lexicographic ordering of thesen-tuples: a)...Ch. 9.6 - d the lexicographic ordering of these strings of...Ch. 9.6 - d the lexicographic ordering of the bit strings...Ch. 9.6 - w the Hasse diagram for the greater than or equal...Ch. 9.6 - w the Hasse Diagram for the less than or equal to...Ch. 9.6 - Prob. 22ECh. 9.6 - Prob. 23ECh. 9.6 - w the Hasse diagram for inclusion on the...Ch. 9.6 - Exercises 25-27 list all ordered pairs in the...Ch. 9.6 - Exercises 25-27 list all ordered pairs in the...Ch. 9.6 - Exercises 25-27 list all ordered pairs in the...Ch. 9.6 - What is the covering relation of the partial...Ch. 9.6 - What is the covering relation of the partial...Ch. 9.6 - What is the covering relation of the partial...Ch. 9.6 - w that a finite poset can be reconstructed from...Ch. 9.6 - wer these questions for the partial order...Ch. 9.6 - wer these questions for the poset ({3, 5,9, 15,...Ch. 9.6 - wer these questions for the poset ({2, 4, 6, 9,...Ch. 9.6 - wer these questions for the poset ({{1}, {2}, {4},...Ch. 9.6 - Prob. 36ECh. 9.6 - Show that lexicographic order is a partial...Ch. 9.6 - w that lexicographic order is a partial ordering...Ch. 9.6 - Suppose that (S,1) and (T,2) are posets. Show...Ch. 9.6 - a) Show that there is exactly one greatest element...Ch. 9.6 - a) Show that there is exactly one maximal element...Ch. 9.6 - a) Show that the least upper bound of a set in a...Ch. 9.6 - Determine whether the posets with these Hasse...Ch. 9.6 - Prob. 44ECh. 9.6 - Show that every nonempty finite subset of a...Ch. 9.6 - Show that if the poset (S,R) is a lattice then the...Ch. 9.6 - a company, the lattice model of information flow...Ch. 9.6 - Prob. 48ECh. 9.6 - Show that the set of all partitions of a set S...Ch. 9.6 - Show that every totally ordered set is a lattice.Ch. 9.6 - Show that every finite lattice has a least element...Ch. 9.6 - Give an example of an infinite lattice with a)...Ch. 9.6 - Prob. 53ECh. 9.6 - ermine whether each of these posets is...Ch. 9.6 - Prob. 55ECh. 9.6 - Show that dense poset with at least two elements...Ch. 9.6 - Show that the poset of rational numbers with the...Ch. 9.6 - Show that the set of strings of lowercase English...Ch. 9.6 - Prob. 59ECh. 9.6 - w that a finite nonempty poset has a maximal...Ch. 9.6 - Find a compatible total order for the poset with...Ch. 9.6 - d a compatible total order for the divisibility...Ch. 9.6 - Find all compatible total orderings for the poset...Ch. 9.6 - Find all compatible total orderings for the poset...Ch. 9.6 - Find all possible orders for completing the tasks...Ch. 9.6 - Schedule the tasks needed to build a house, by...Ch. 9.6 - Prob. 67ECh. 9 - Prob. 1RQCh. 9 - a) What is a reflexive relation? b) What is a...Ch. 9 - e an example of a relation on the set {1, 2,3,4}...Ch. 9 - a) How many reflexive relations are there on a set...Ch. 9 - a) Explain how ann-ary relation can be used to...Ch. 9 - a) Explain how to use a zero-one matrix to...Ch. 9 - a) Explain how to use a directed graph to...Ch. 9 - a) Define the reflexive closure and the symmetric...Ch. 9 - a) Define the transitive closure of a relation. b)...Ch. 9 - a) Define an equivalence relation. b) Which...Ch. 9 - a) Show that congruence modulo in is an...Ch. 9 - a) What are the equivalence classes of an...Ch. 9 - lain the relationship between equivalence...Ch. 9 - a) Define a partial ordering. b) Show that the...Ch. 9 - Explain how partial orderings on the...Ch. 9 - a) Explain how to construct the Hasse diagram of a...Ch. 9 - a) Define a maximal element of a poset and the...Ch. 9 - Prob. 18RQCh. 9 - a) Show that every finite subset of a lattice has...Ch. 9 - a) Define a well-ordered set. b) Describe an...Ch. 9 - Let S be the set of all stings of English leers....Ch. 9 - struct a relation on the set {a,b, c, d} that is...Ch. 9 - Show that the relationRonZZdefined by (a, b)R(c,...Ch. 9 - w that a subset of an antisymmetric relation is...Ch. 9 - LetRbe a reflexive relation on a setA. Show...Ch. 9 - Suppose thatR1andR2are reflexive relations on a...Ch. 9 - pose thatR1andR2are reflexive relations on a...Ch. 9 - Suppose that R is a symmetric relation on a set A....Ch. 9 - R1andR2be symmetric relations. IsR1R2also...Ch. 9 - A relationRis called circular ifaRbandbRcimply...Ch. 9 - Show that a primary key in ann-ary relation is a...Ch. 9 - Is the primary key in ann-ary relation also a...Ch. 9 - Show that the reflexive closure of the symmetric...Ch. 9 - Rbe the relation on the set of all mathematicians...Ch. 9 - a) Give an example to show that the transitive...Ch. 9 - a) LetSbe the set of subroutines of a computer...Ch. 9 - pose thatRandSare relations on a set A withRSsuch...Ch. 9 - Show that the symmetric closure of the union of...Ch. 9 - Devise an algorithm, based on the concept of...Ch. 9 - ch of these are equivalence relations on the set...Ch. 9 - How many different equivalence relations with...Ch. 9 - Show that{(x,y)xyQ}is an equivalence relation on...Ch. 9 - pose thatP1={A1,A2,....Am}andP2={B1,B2,....Bm}are...Ch. 9 - Prob. 24SECh. 9 - Prob. 25SECh. 9 - Let P(S) be thesetof all partitions of the set S....Ch. 9 - edule the tasks needed to cook a Chinese meal by...Ch. 9 - Find all chains in the posets with the Hass...Ch. 9 - Prob. 29SECh. 9 - Find an antichain with the greatest number of...Ch. 9 - Show that every maximal chain in a finite poset...Ch. 9 - Prob. 32SECh. 9 - w that in any group ofmn+1people there is either a...Ch. 9 - Prob. 34SECh. 9 - Prob. 35SECh. 9 - Prob. 36SECh. 9 - Prob. 37SECh. 9 - LetRbe a quasi-ordering and let S be the relation...Ch. 9 - w that the following properties hold for all...Ch. 9 - w that ifxandyare elements of a...Ch. 9 - w that ifLis a bounded lattice with upper bound 1...Ch. 9 - w that every finite lattice is bounded. A lattice...Ch. 9 - Give an example of a lattice that is not...Ch. 9 - Show that the lattice(P(S),)whereP(S) is the power...Ch. 9 - the lattice (Z+,)distributive? The complement of...Ch. 9 - Give an example of a finite lattice where at least...Ch. 9 - w that the lattice(P(S))whereP(S)is the power set...Ch. 9 - Show that ifLis a finite distributive lattice,...Ch. 9 - w that the game of Chomp with cookies arranged in...Ch. 9 - w that if(S,)has a greatest elementb,then a...Ch. 9 - Prob. 1CPCh. 9 - Prob. 2CPCh. 9 - Prob. 3CPCh. 9 - Prob. 4CPCh. 9 - Prob. 5CPCh. 9 - Prob. 6CPCh. 9 - Prob. 7CPCh. 9 - Prob. 8CPCh. 9 - Prob. 9CPCh. 9 - Given the matrix representing relation on a finite...Ch. 9 - Prob. 11CPCh. 9 - en the matrix representing a relation on a finite...Ch. 9 - Given the matrix representing a relation on a...Ch. 9 - Prob. 14CPCh. 9 - Prob. 15CPCh. 9 - Prob. 1CAECh. 9 - Prob. 2CAECh. 9 - Prob. 3CAECh. 9 - Prob. 4CAECh. 9 - d the transitive closure of a relation of your...Ch. 9 - pute the number of different equivalence relations...Ch. 9 - Prob. 7CAECh. 9 - Prob. 8CAECh. 9 - Prob. 9CAECh. 9 - Discuss the concept of a fuzzy relation. How are...Ch. 9 - cribe the basic principles of relational...Ch. 9 - Explain how the Apriori algorithm is used to find...Ch. 9 - Describe some applications of association rules in...Ch. 9 - Prob. 5WPCh. 9 - Prob. 6WPCh. 9 - Prob. 7WPCh. 9 - Prob. 8WPCh. 9 - Prob. 9WPCh. 9 - Prob. 10WPCh. 9 - Prob. 11WPCh. 9 - Prob. 12WP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Determine whether the following value is a continuous random variable, discrete random variable, or not a random variable. a. The amount of rain in City A during July b. The hair color of adults in the United States c. The weight of a hamburger d. The number of people with blood type B in a random sample of 13 people e. The number of runs scored during a baseball game f The number of nigeons in a country a. Is the amount of rain in City A during July a discrete random variable, continuous random variable, or not a random variable? A. It is a continuous random variable. B. It is a discrete random variable. C. It is not a random variable. b. Is the hair color of adults in the United States a discrete random variable, continuous random variable, or not a random variable? A. It is a discrete random variable. B. It is a continuous random variable. C. It is not a random variable. c. Is the weight of a hamburger a discrete random variable, continuous random variable, or not a random variable?…arrow_forwardExercise 12.2. Let F be a field and n Є N. (1) For every subset S of F", show that I(S) := {f(x1, . ,xn) Є F[x1,...,xn] | f (a₁,, an) = 0, V(a1, ..., an) E S} is an ideal of the polynomial ring F[x1, ..., xn], called the vanishing ideal of S. (2) Given two subsets S and T of F", prove or disprove that I(SUT) = I(S)NI(T) · and I(SNT) = I(S) + I(T).arrow_forwardAssume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of 0 and a standard deviation of 1. Draw a graph and find the probability of a bone density test score greater than 0.86. ... Sketch the region. Choose the correct graph below. ○ A. ^ -0.86 B. D. 0.86 0.86 -0.86 0.86 The probability is (Round to four decimal places as needed.)arrow_forward
- A genetic experiment with peas resulted in one sample of offspring that consisted of 444 green peas and 167 yellow peas. a. Construct a 95% confidence interval to estimate of the percentage of yellow peas. b. Based on the confidence interval, do the results of the experiment appear to contradict the expectation that 25% of the offspring peas would be yellow? a. Construct a 95% confidence interval. Express the percentages in decimal form. ☐arrow_forwardDetermine whether the study is an experiment or an observational study, and then identify a major problem with the study. A sociologist has created a brief survey to be given to 2000 adults randomly selected from the U.S. population. Here is her first question: Have you ever been the victim of a felony crime? This is an individuals. because the researcher What is a major problem with the study? A. There is no blinding or replication, which has a high chance of leading to bias. B. There may be individuals that do not answer the question honestly. C. The responses will be voluntary, which will lead to a high chance of bias. D. The sample includes only U.S. adults. thearrow_forwardA claim is made that the proportion of children who play sports is less than 0.5, and the sample statistics include n = 1320 subjects with 30% saying that they play a sport. What is the null hypothesis? Find the value of the test statistic z. !!! B I U S TX = = = Xz x² Insert Formulaarrow_forwardListed below are the lead concentrations (in µg/g) measured in different Ayurveda medicines. Ayurveda is a traditional medical system commonly used in India. The lead concentrations listed here are from medicines manufactured in the United States. Assume that a simple random sample has been selected. Use a 0.10 significance level to test the claim that the mean lead concentration for all such medicines is less than 14.0 µg/g. 3.03 6.47 6.01 5.51 20.53 7.51 12.04 20.48 11.53 17.51 Identify the null and alternative hypotheses. Ho: H₁: (Type integers or decimals. Do not round.) Identify the test statistic. (Round to two decimal places as needed.) Identify the P-value. ... (Round to three decimal places as needed.) State the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. the null hypothesis. There sufficient evidence at the 0.10 significance level to the claim that the mean lead concentration for all Ayurveda medicines manufactured…arrow_forwardThe following frequency distribution represents the scores on a math test. Find the class midpoint of scores for the interval 50-59. BIUS Ix Scores 50-59 E Xz Insert Formula Number of students 2 60-69 70-79 80-89 4 6 15 90-99 5arrow_forwardWhich of the following is NOT a property of the chi-square distribution? Choose the correct answer below. ... A. The mean of the chi-square distribution is 0. B. The chi-square distribution is different for each number of degrees of freedom. C. The chi-square distribution is not symmetric. D. The values of chi-square can be zero or positive, but they cannot be negative.arrow_forwardD2L Course Schedule × ⇒ Math 140 AC2 MT × G Google ☑ Untitled documen × G Google G square root sign ✗ adidas Samba OG X Math 140 AC2 MT X → C https://drive.google.com/file/d/1pXqJ_6k8OigXg6qML2lkxIM-bDwLhk5T/view 3. We're a little past the halfway point of the semester. I've been thinking about how we've been doing. I have noticed something interesting about the relationship between WAs and grades. I made a piecewise function to describe the situation. G(x) is the grade for someone who has completed x WAs. Use the function for parts a-c. (7.5 pts.) 20 for x=0 G(x)=15x+ 30 for 0arrow_forward3 Let F = (y² + z³, x³ + z², xz). Evaluate Saw F ds for each of the following regions W: A. x² + y² ≤ x ≤ 6 B. x² + y² ≤ z < 6, x ≥ 0 c. x² + y² ≤ z ≤ 6, x ≤ 0arrow_forwardYou are interested in the difference between two population means. Both populations are normally distributed, and the population variances σ1212 and σ2222 are known. You use an independent samples experiment to provide the data for your study. What is the appropriate test statistic? t = x̄Dx̄D/ √[sD2sD2(1/n1n1 + 1/n2n2)] F = s1s1/s2s2 z = (x̄1x̄1 – x̄2x̄2) / √[σ1212/n1n1 + σ2222/n2n2] t = (x̄1x̄1 – x̄2x̄2) / √[sp2sp2(1/n1n1 + 1/n2n2)] Suppose instead that the populations are not normally distributed. The test statistic given is still appropriate provided that . You are interested in the difference between two population means. The population variances σ1212 and σ2222 are unknown and equal. You use an independent samples experiment to generate the data for your study, and each of your samples meet the large sample requirement. What is the appropriate test statistic? z = (x̄1x̄1 – x̄2x̄2) / √[σ1212/n1n1 + σ2222/n2n2] t =…arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage LearningGlencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillHolt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGALAlgebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
What is a Relation? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=hV1_wvsdJCE;License: Standard YouTube License, CC-BY
RELATIONS-DOMAIN, RANGE AND CO-DOMAIN (RELATIONS AND FUNCTIONS CBSE/ ISC MATHS); Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=u4IQh46VoU4;License: Standard YouTube License, CC-BY