
Concept explainers
Determine the mass moment of inertia of the steel fixture shown with respect to (a) the x axis, (b) the y axis, (c) the z axis. (The density of steel is 7850 kg/m3.)
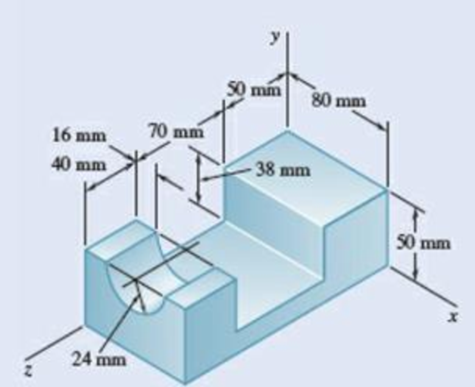
Fig. P9.145
(a)
Find the mass moment of inertia with respect to x axis.
Answer to Problem 9.145P
The mass moment of inertia with respect to x axis is
Explanation of Solution
Given information:
The density
Calculation:
Sketch the section of steel fixture as shown in Figure 1.
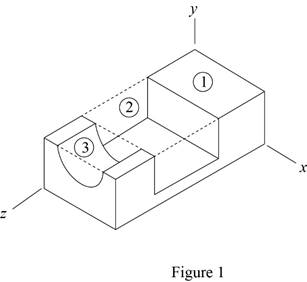
Find the mass
Here, V is volume of rectangular section 1.
Modify Equation (1).
Here, w is the width of the section 1, l is the length of the rectangular section 1, and t is the thickness of the section 1.
Substitute
Find the mass
Here, V is volume of rectangular section 2.
Modify Equation (3).
Here, w is the width of the section 2, l is the length of the rectangular section 2, and t is the thickness of the section 2.
Substitute
Find the mass
Substitute
Refer to Figure 9.28, “Mass moment of inertia for common geometric shapes” in the text book.
Find the mass moment of inertia with respect to x axis as shown below:
Convert the dimension in mm to m.
Similarly calculate the remaining values.
Substitute
Thus, the mass moment of inertia with respect to x axis is
(b)
Find the mass moment of inertia with respect to y axis.
Answer to Problem 9.145P
The mass moment of inertia with respect to y axis is
Explanation of Solution
Calculation:
Find the mass moment of inertia with respect to y axis as shown below:
Convert the dimensions in mm to m.
Substitute
(c)
Find the mass moment of inertia with respect to z axis.
Answer to Problem 9.145P
The mass moment of inertia with respect to z axis is
Explanation of Solution
Calculation:
Find the mass moment of inertia with respect to z axis as shown below:
Convert the dimensions in mm to m.
Substitute
Want to see more full solutions like this?
Chapter 9 Solutions
VEC MECH 180-DAT EBOOK ACCESS(STAT+DYNA)
- Using properties of a saturated water, explain how you would determine the mole fraction of water vapor at the surface of a lake when the temp of the lake surface and the atmospheric pressure are specified.arrow_forwardConsider a glass of water in a room at 15 degrees C and 97 kPa. If the relative humidity in the room is 100 percent and the water and the air are in thermal and phase equilibrium, determine the mole fraction of the water vapor in the air and the mole fraction of air in the water.arrow_forwardStaring with an energy balance on a cylindirical shell volume element, derive the steady one dimensional heat conduction equation for a long cylinder with constant thermal conductivity in which heat is generated at a rate of egen.arrow_forward
- Consider a round potato being baked in an oven. Would you model the heat transfer to the potato as one, two, or three dimensional? Would the heat transfer be steady or transient? Also, which coordinate system would you use to solve this problem, and where would you place the origin? Explain.arrow_forward0 = 6 a = 25 t = 3 Y b = 30 xarrow_forwardSolve this problem and show all of the workarrow_forward
- No chatgpt pls will upvotearrow_forwardreading is 0.4 mas SHOWN. Assume h₁ = 0.4 m, h₂ = 0.5 m. (a) Do you know the specific weight of mercury? (b) Do you know the specific weight of gasoline? (c) Do you know the specific weight of oil? (a) YHg = 133,000 (b) Ygas = 6867 (c) Yoil = 8829 eTextbook and Media Part 2 N/m³ N/m³ N/m³ A+ Gasoline t +B Oil -Mercury Attempts: unlimited Did you calculate the pressure difference between two locations using the correct specific weight? Did you assume that the pressures in fluid are the same in a horizontal plane even though they are in different tubes? Are the calculated pressures in a column of fluid always higher at lower elevations? Did you account for the fact that the two horizontal tubes of the U-tube are above the ground? Concepts: The pressure in a fluid is a function of the specific weight of the fluid and the height relative to a reference. Pressure is constant in a horizontal plane of a continuous mass of fluid. (a) What is the initial pressure difference? (PA-PB) (b) What is…arrow_forwardFind the solution of the following Differential Equations 1) "-4y+3y=0 3) "+16y=0 2) y"-16y=0 4) y"-y-6y=0 5) y"+2y=0 7) y"+y=0, (#0) 9) y"-y=0, y(0) = 6, y'(0) = -4 11) y"-4y+3y=0, y(0)=-1, 13) y'(0) = -5 "+2y+2y=0 15) y"-9y=0 17) y"-4y=0 6) y"-2y+2y=0 8) "+4y+5y=0 10) y"-9y=0, y(0) = 2, y'(0) = 0 12) y"-3y+2y= 0, y(0)=-1, y'(0) = 0 14) 4y+4y+y=0 16) "+6y+12y=0 18) 4y+4y+17y=0arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





