
Concept explainers
(a)
Find the principal mass moment of inertia of the cylinder at the origin O.
(a)
Answer to Problem 9.183P
The principal moment of inertia are
Explanation of Solution
Given information:
Refer Problem 9.168.
Show the moment of inertia as follows:
Calculation:
Show the Equation 9.56 as follows:
Substitute
Consider the value of
Solve the above Equation and get the value of
The principal moment of inertia are
Thus, The principal moment of inertia are
(b)
Find the angles made by the principal axis of inertia at O with the coordinate axis.
Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis.
(b)
Answer to Problem 9.183P
The angles made by the principal axis of inertia at O with the coordinate axis is,
Explanation of Solution
Given information:
Consider the direction cosines of each principal axis are denoted by
Calculation:
Refer Part (a).
Consider K1.
Show the Equation 9.54 as follows:
Substitute
Solve Equation (2).
Get the value of
Show the Equation 9.57 as follows:
Solve above Equation and get the value of
Show the direction cosines
Consider K2.
Show the Equation 9.54 as follows:
Substitute
Solve Equation (4).
Get the value of
Show the Equation 9.57 as follows:
Solve above Equation and get the value of
Show the direction cosines
Consider K3.
Show the Equation 9.54 as follows:
Substitute
Solve Equation (6).
Get the value of
Show the Equation 9.57 as follows:
Solve above Equation and get the value of
Show the direction cosines
The angles made by the principal axis of inertia at O with the coordinate axis is,
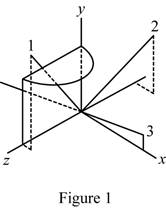
Sketch the body and show the orientation of the principal axis of inertia relative to x, y, and z axis as shown in Figure 1.
Want to see more full solutions like this?
Chapter 9 Solutions
VEC MECH 180-DAT EBOOK ACCESS(STAT+DYNA)
- Qu 2 Calcium oxide (CaO) a white, caustic, alkaline solid that reacts vigorously with water to produce calcium hydroxide, releasing heat in the process. It is used in various industrial applications, including cement production and water treatment. The ionic radii of the ions are: TCa2+= 0.100 nm and roz-= 0.140 nm. On the basis of this information answer the following questions:Number 1 through 4 I need to show all work step by step problemsarrow_forwardShow work if any equations or calculations are used. Assuming hole basis, find the shaft and hole dimensions for a sliding fit using a basic hole size of 20mm. Show the max and minimum size for both hole and shaft. Utilize the equations and tables in the appendix.arrow_forwardShow work if any equations or calculations are used. A milling machine is equipped with a 1” diameter end mill. During a facingoperation, the spindle is running at 275 RPM. The depth of cut is 0.04” and linear feed rate is 2” per minute. Find: (a) Cutting speed, (b) Material Removal Ratearrow_forward
- L1 = 5.7m, L2 = 1m, L3 = 1.2m, L4 = 1m, L5 = 0.2, L6 = 0.5m, v2 = 4.8m/s. The solutions should include, but not be limited to, the equations used tosolve the problems, the charts used to solve the problems, detailed working,choice of variables, the control volume considered, justification anddiscussion of results etc.If determining the friction factor, the use of both Moody chart and empiricalequations should be used to verify the validity of the valuearrow_forwardPlease identify the marked points of the stress-strain curve (Write on graph next to corresponding letter) Stress, σ A D (slope of line) B. C Strain, &arrow_forwardr Q2. A bracket is attached to a vertical column by means of six identical bolts as shown in Fig. 1. It is subjected to an eccentric force of P-80 kN at a distance of 200 mm from the center of column. What is the magnitude of maximum shear force and which bolt carry it? P= 80 kN 200 Fig. 1 1 2- 75 6 30 75 → 5 .5 1- 50 10-50-1arrow_forward
- 3. The attachment shown in the Fig.2 is made of 1040 HR. The static force is 30 kN. Specify the weldment (give the pattern, electrode number, type of weld, length of weld, and leg size). 30 kN Fig. 2 500 All dimension in mm 100 (15 marks)arrow_forwardฉันต้องการหา อุณหภูมิสุดท้ายของกระบวนการนี้และงานของกระบวนการนี้มีค่าเท่าใดarrow_forwardThe pressure and temperature at the beginning of compression of a cold air-standard Diesel cycle are 100 kPa and 300 K , respectively. At the end of the heat addition, the divssure is 7.2 MPa and the temperature is 2050 K . Assume constant specific heats evaluated at 300 K . Determine:(a) the compression ratio.(b) the cutoff ratio.(c) the percent thermal efficiency of the cycle.(d) the mean effective pressure, in kPa .arrow_forward
- Q3. Determine the reaction force at A and force P applied at 45° to the horizontal just necessary to start a roller 100 cm diameter over an obstruction 25 cm high, if the roller weighs 1000 N, as shown in Fig. 3. Fig. (3)arrow_forwardCorrect Answer is written below(preferably handwritten solution) . Detailed and complete fbd only please. I will upvote, thank you.arrow_forwardThe pressure and temperature at the beginning of compression of a cold air-standard Diesel cycle are 100 kPa and 300 K , respectively. At the end of the heat addition, the pressure is 7.2 MPa and the temperature is 2050 K . Assume constant specific heats evaluated at 300 K . Determine:(a) the compression ratio.(b) the cutoff ratio.(c) the percent thermal efficiency of the cycle.(d) the mean effective pressure, in kPaarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





