8th Edition

ISBN: 9781260521337

Author: ROSEN

Publisher: MCG

See similar textbooks

Videos

Textbook Question

Chapter 9.5, Problem 43E

ch of these collections of subsets are partitions of the set of bit strings of length 8?

a) the set of bit strings that begin with 1, the set of bit strings that begin with 00, and the set of bit strings that begin with 01

b) the set of bit strings that contain the string 00, the set of bit strings that contain the string 01, the set of bit strings that contain the string 10, and the set of bit strings that contain the string 11

c) the set of bit strings that end with 00, the set of bit strings that end with 01, the set of bit strings that end with 10, and the set of bit strings that end with 11

d) the set of bit strings that end with 111, the set of bit strings that end with 011, and the set of bit strings that end with 00

e) the set of bit strings that contain3kones for some nonnegative integerk,the set of bit strings that contain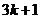 Chapter 9.5, Problem 43E, ch of these collections of subsets are partitions of the set of bit strings of length 8? a) the set , example 1 ones for some nonnegative integerk,and the set of bit strings that contain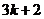ones for some nonnegative integerk.

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 9.5, Problem 42E

Chapter 9.5, Problem 44E

Students have asked these similar questions

If the binary operation * is defined on a set of ordered pairs of real number as (a,b)*(c,d)= (ad+bc, bd) and is associative then (1,2)*(3,5)*(3,4) equals:

Let N= {1, 2, 3, 4, .} be the set of natural numbers and S= (1, 4, 9, 16, ...} be the set of squares of the natural numbers. Then N - S, since we have the one-to-one correspondence 1 + 1, 2 + 4, 3 + 9, 4 + 16, ... n+ n?. (This example is interesting, since it shows that an infinite set can be equivalent to a proper subset of itself.) Show that each of the following pairs of sets are equivalent by carefully describing a one-to-one correspondence between the sets. Complete parts (a) through (c) below. (a) The whole numbers and natural numbers, W = {0, 1, 2, 3, ..} and N= {1, 2, 3, 4, ...} Which of the following describes a one-to-one correspondence between the two sets? O A. For each element in W, there is an element in N that is double that element. O B. For each element in w. there is an element in N that is 1 areater than double that element.

Chapter 9 Solutions

DISCRETE MATHEMATICS+ITS APPL. (LL)-W/A

Ch. 9.1 - t the ordered pairs in the...Ch. 9.1 - a) List all the ordered pairs in the relation R =...Ch. 9.1 - each of these relations on the set {1, 2, 3, 4},...Ch. 9.1 - ermine whether the relationRon the set of all...Ch. 9.1 - ermine whether the relationRon the set of all Web...Ch. 9.1 - ermine whether the relationRon the set of all real...Ch. 9.1 - ermine whether the relationRon the set of all...Ch. 9.1 - w that the relationR=Oon a nonempty set S is...Ch. 9.1 - Show that the relationR=on the empty setS=is...Ch. 9.1 - e an example of a relation on a set that is a)...

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.

Solution Summary: The author explains that partition sets are partitions of bit strings of length 8, where X is a disjoint union of the subsets

Videos

Want to see the full answer?

Chapter 9 Solutions