The Heart of Mathematics: An Invitation to Effective Thinking, WileyPLUS NextGen Card with Loose-leaf Set Single Semester: An Invitation to Effective Thinking (Key Curriculum Press)
4th Edition
ISBN: 9781119760054
Author: Burger, Edward B. , Starbird, Michael
Publisher: Wiley (WileyPLUS Products)
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 9.4, Problem 16MS
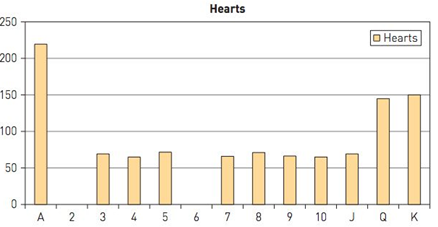
House of cards. Your friend hands you a deck of 52 cards along with the histogram below. It shows the results for hearts if a card is chosen at random from the deck, its rank recorded
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Given ƒ = (10, -10) and q = (-8, −7), find ||ƒ— q||
and
dƒ-9.
Give EXACT answers. You do NOT have to simplify your radicals!
Suppose that a driver's test has a mean score
of 7 (out of 10 points) and standard deviation
0.5.
a. Explain why you can reasonably assume
that the data set of the test scores is
mound-shaped.
b. For the drivers taking this particular test,
where should 68 percent of them score?
c. Where should 95 percent of them score?
d. Where should 99.7 percent of them score?
S
13
Can the mean of a data set be higher than
most of the values in the set? If so, how? Can
the median of a set be higher than most of
the values? If so, how?
srit to esta
Chapter 9 Solutions
The Heart of Mathematics: An Invitation to Effective Thinking, WileyPLUS NextGen Card with Loose-leaf Set Single Semester: An Invitation to Effective Thinking (Key Curriculum Press)
Ch. 9.1 - Embarrassing data. Suppose you asked 100 students...Ch. 9.1 - Hugging both parents (S). You ask 150 students to...Ch. 9.1 - Short test. To save time grading, a professor asks...Ch. 9.1 - Computer polls. Suppose dot-corn entrepreneurs...Ch. 9.1 - Voluntary grade inflation. The dean felt that a...Ch. 9.1 - Pornography (ExH). Suppose you asked 100 students...Ch. 9.1 - Cartoons. Suppose 380 students out of 1000 still...Ch. 9.1 - Bias beef (H). Suppose you have an assignment to...Ch. 9.1 - Drug data (ExH). You ask 250 students to answer...Ch. 9.1 - Kissing. You ask 180 students to answer the...
Ch. 9.1 - Cheating (S). Suppose 60 students out of 200...Ch. 9.1 - Dental hygiene. Suppose you want to know how often...Ch. 9.1 - More homework. In a recent survey of random...Ch. 9.1 - PBS. In the old days, the Nielsen ratings of...Ch. 9.1 - 9:00 AM versus 9:00 PM (H). You take a survey of...Ch. 9.1 - Internet askew. Find ads or articles on the Web...Ch. 9.1 - Sleazy survey (H). The mayor of a city seeks to...Ch. 9.1 - Bread winners? You want to know in what percentage...Ch. 9.1 - Beemer babies (H). You want to estimate what...Ch. 9.1 - Coffee, tea, or milk? Youre considering whether to...Ch. 9.1 - The dog pound. Otis the puppy grew approximately...Ch. 9.1 - Hows that again? An ambitious politician in your...Ch. 9.1 - Smells like team spirit. A losing basketball team...Ch. 9.1 - Stack me timbers. Every October, students from the...Ch. 9.1 - Risky business (H). In a psychology class, the...Ch. 9.1 - Risky II. The psychology instructor from the...Ch. 9.2 - Internet costs. Make a histogram of the data on...Ch. 9.2 - Internet costs—summaries (S). Find the mean and...Ch. 9.2 - Internet costs-more summaries. Compute the...Ch. 9.2 - How variable. Remember that the standard deviation...Ch. 9.2 - Pie or no pie. Below are two graphical...Ch. 9.2 - Stats on steroids. Harry Bonds and Mark McGwire...Ch. 9.2 - Whos the best—short summary. For the home-run...Ch. 9.2 - Will tomorrow be different? At the beginning of...Ch. 9.2 - How different are they? (S) The following...Ch. 9.2 - Whats normal? The histograms of three data sets...Ch. 9.2 - Check the bounce (ExH). Until 1992, members of...Ch. 9.2 - College data. Using the student survey data given...Ch. 9.2 - News data. Find some data in a recent newspaper or...Ch. 9.2 - Which half? Half of the people in the United...Ch. 9.2 - Grades. A student received the following quiz...Ch. 9.2 - Raising scores (ExH). A student received the...Ch. 9.2 - Mean and median (S). Give an example of a data set...Ch. 9.2 - Median and mean. Give an example of a data set...Ch. 9.2 - Some taxing statistics (H). Politicians love to...Ch. 9.2 - Whoops. Find an example in a recent newspaper or...Ch. 9.2 - Further whoops (H). A survey of 100 recent college...Ch. 9.2 - Is this normal? Suppose the data in the previous...Ch. 9.2 - Average the grades. In a math class of 23 men and...Ch. 9.2 - Taxes(ExH). Find an effective graphical...Ch. 9.2 - Kids in the hall. You have three cousins with mean...Ch. 9.2 - Testing the data. A math instructor reports the...Ch. 9.2 - One mean mean. Suppose an instructor reports exam...Ch. 9.2 - Home sweet home. For a political science project,...Ch. 9.2 - No back up (H). You have 120 pieces of data. They...Ch. 9.3 - I.D. please. Identify the Distributions below as...Ch. 9.3 - Deviating from the norm (H). The following three...Ch. 9.3 - Match quest. The following three data sets are...Ch. 9.3 - Doubt the dice. You have four different dice and...Ch. 9.3 - More matching. A class was quizzed on two...Ch. 9.3 - Gas guzzling. In the One-Die Random Gas Station...Ch. 9.3 - Dr Die. Suppose you doctor a standard six-sided...Ch. 9.3 - Dr. Mean (S). What is the mean roll you would...Ch. 9.3 - A podiatrist in the making. Suppose you ask the...Ch. 9.3 - Beanie babies (S). All freshmen entering...Ch. 9.3 - Retiring standards (ExH). A classmate describes a...Ch. 9.3 - Unseasonable weather. The average high temperature...Ch. 9.3 - Are you normal? Which of the following data sets...Ch. 9.3 - Warming Up? (H) Suppose we measure the temperature...Ch. 9.3 - Possibly uniform. Which of the following data sets...Ch. 9.3 - Under the normally spreading chestnut tree. A...Ch. 9.3 - Abnormal. Give two example of data sets from your...Ch. 9.3 - Heavry petting. You adopt a kitten from the animal...Ch. 9.3 - Less than normal. Here are some distributions that...Ch. 9.3 - Gas guzzling (ExH). Consider the Two-Dice Random...Ch. 9.3 - The 68-95-99.7rule. Referring back to a discussion...Ch. 9.3 - Heads up. The marching band is getting new...Ch. 9.3 - Knees up. Building on the previous Mindscape,...Ch. 9.3 - Mother Brown (H). The most popular pizza place...Ch. 9.3 - Scoring some Zs. Refer to the formula for the...Ch. 9.3 - 2Catchin some Zs. You happen to know the z-score...Ch. 9.4 - Sophomore survey. You want to survey all students...Ch. 9.4 - IntenaI confidence. Which of the following best...Ch. 9.4 - Voting bodies. Calculate the percentage of the...Ch. 9.4 - Play the percentages. If n=100, what is the value...Ch. 9.4 - Play the percentages backwards (S). If 1n=0.05...Ch. 9.4 - Election up for grabs. In the upcoming election...Ch. 9.4 - U.S. samples (S). Suppose you can be quite...Ch. 9.4 - Bigger confidence? Suppose a pollster reports that...Ch. 9.4 - Overlapping confidence. Suppose two surveys are...Ch. 9.4 - Does size matter? (ExH) You want to gather data...Ch. 9.4 - More voting bodies (H). You want to gather data...Ch. 9.4 - National poll. Suppose you do polling in each of...Ch. 9.4 - Dizzy Lincoln. The text describes a penny-spinning...Ch. 9.4 - Hire a consultant. A consulting firm analyzed...Ch. 9.4 - House of cards. Your friend hands you a deck of 52...Ch. 9.4 - A fish story (ExH). You are a biologist sampling...Ch. 9.4 - Political gamble. The mayor of a small city has...Ch. 9.4 - The power of placebo. A study of pain relief...Ch. 9.4 - Marge Innoverra. You test 100 light bulbs randomly...Ch. 9.4 - How many math students does it take …(S). How...Ch. 9.4 - … to screw in a lightbulb? How many light bulbs...Ch. 9.4 - Snack sample (H). A survey asking students whether...Ch. 9.4 - Stop the study (ExH). A 2006 NIH study of...Ch. 9.4 - The sniff test. In 2004 the British Medical...Ch. 9.4 - Roving report. In 2006 there was a scandal...Ch. 9.4 - Polling roundup (H). A polling organization wants...Ch. 9.4 - Rodent roundup. Your psychology class is planning...Ch. 9.4 - Even more confident. Mindscape 27 gives a more...Ch. 9.4 - ESP. Your psychology class does some experiments...Ch. 9.4 - Trying trials. Your roommate is supervising an...Ch. 9.5 - Mendels snapdragons. Another of Mendels...Ch. 9.5 - Telephone/soda twins. Suppose your school has 1000...Ch. 9.5 - Correlation comparison. Below are three...Ch. 9.5 - Percent practice. Convert the fractions below to...Ch. 9.5 - Family dinner. Recent studies have reported on the...Ch. 9.5 - More Mendel (S). Given Mendels snapdragon...Ch. 9.5 - Oedipus red. Given Mendels work described in...Ch. 9.5 - Oedipus white. Given Mende1 work described in...Ch. 9.5 - Prob. 9MSCh. 9.5 - Astrology. An experiment is done to test the value...Ch. 9.5 - Stressful diet. One hundred young women were given...Ch. 9.5 - Abstinence evidence? President George W. Bush...Ch. 9.5 - Matching correlations. Below are some scatterplots...Ch. 9.5 - Fast data (H). If you plot the wining Olympic mens...Ch. 9.5 - College town. You go to school in a college town....Ch. 9.5 - Car count (S). You wonder how many cars there are...Ch. 9.5 - For Mindscapes 19-22, say whether or not each is...Ch. 9.5 - For Mindscapes 19-22, say whether or not each is...Ch. 9.5 - For Mindscapes 19-22, say whether or not each is...Ch. 9.5 - For Mindscapes 19-22, say whether or not each is...Ch. 9.5 - Mendel genealogy (H). We return once again to...Ch. 9.5 - Martian genetics. A certain alien species has...Ch. 9.5 - More Martians. Given the scenario from the...Ch. 9.5 - Politics as usual. During the presidential...Ch. 9.5 - Going postal. Your company will sign a contract...Ch. 9.5 - Fast paradox (ExH). The correlation between year...Ch. 9.5 - Up and down. In the past year, the grade point...Ch. 9.5 - Modified Mendel. We again return to Mendel...Ch. 9.5 - Going extinct. A paleontologist has gathered data...Ch. 9.5 - Diners delight. There are five dining halls on...Ch. 9.5 - The candy man. Your math instructor brings a...Ch. 9.5 - The candy jars. Your math instructor brings two...Ch. 9.5 - Correlated chorus (H). The chorus has data on the...Ch. 9.5 - Correlated Britney. The Britney S. Fan Club has...
Additional Math Textbook Solutions
Find more solutions based on key concepts
The equivalent expression of x(y+z) by using the commutative property.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...
College Algebra with Modeling & Visualization (5th Edition)
Read about basic ideas of statistics in Common Core Standards for grades 3-5, and discuss why students at these...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Student Ages The mean age of all 2550 students at a small college is 22.8 years with a standard deviation is 3....
Introductory Statistics
Fill in each blank so that the resulting statement is true. Any set of ordered pairs is called a/an ____.The se...
Algebra and Trigonometry (6th Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- you stop recording velocity data at t = 4.0s but you notice a short time later that your friend going fast at 13.8m/s. assuming he keeps the same acceleration, how much time passed since you stopped recording dataarrow_forwardGiven the vector v→=⟨3,-5⟩, find the magnitude and angle in which the vector points (measured in radians counterclockwise from the positive x-axis and 0≤θ<2π). Round each decimal number to two places.arrow_forwardGiven sets X and Y with X ∈ Y, is it always true that P (X) ∈ P (Y) (power sets)? If not, what is a counterexample?arrow_forward
- A random variable X takes values 0 and 1 with probabilities q and p, respectively, with q+p=1. find the moment generating function of X and show that all the moments about the origin equal p. (Note- Please include as much detailed solution/steps in the solution to understand, Thank you!)arrow_forward1 (Expected Shortfall) Suppose the price of an asset Pt follows a normal random walk, i.e., Pt = Po+r₁ + ... + rt with r₁, r2,... being IID N(μ, o²). Po+r1+. ⚫ Suppose the VaR of rt is VaRq(rt) at level q, find the VaR of the price in T days, i.e., VaRq(Pt – Pt–T). - • If ESq(rt) = A, find ES₁(Pt – Pt–T).arrow_forward2 (Normal Distribution) Let rt be a log return. Suppose that r₁, 2, ... are IID N(0.06, 0.47). What is the distribution of rt (4) = rt + rt-1 + rt-2 + rt-3? What is P(rt (4) < 2)? What is the covariance between r2(2) = 1 + 12 and 13(2) = r² + 13? • What is the conditional distribution of r₁(3) = rt + rt-1 + rt-2 given rt-2 = 0.6?arrow_forward
- 3 (Sharpe-ratio) Suppose that X1, X2,..., is a lognormal geometric random walk with parameters (μ, o²). Specifically, suppose that X = Xo exp(rı + ...Tk), where Xo is a fixed constant and r1, T2, ... are IID N(μ, o²). Find the Sharpe-ratios of rk and log(Xk) — log(Xo) respectively, assuming the risk free return is 0.arrow_forwardi need help with question 2arrow_forwardNumerical anarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
what is Research Design, Research Design Types, and Research Design Methods; Author: Educational Hub;https://www.youtube.com/watch?v=LpmGSioXxdo;License: Standard YouTube License, CC-BY