
a.
Compute the differences in samples of matched pairs Sample-1– Sample-2.
a.
Answer to Problem 10E
The differences in samples of matched pairs Sample-1– Sample-2 is,
| S.no | Difference |
| 1 | –6 |
| 2 | –1 |
| 3 | –9 |
| 4 | –1 |
| 5 | –5 |
| 6 | –1 |
| 7 | –4 |
| 8 | –8 |
| 9 | –2 |
| 10 | –9 |
Explanation of Solution
Calculation:
The data represents the sample of a five matched pairs.
Let
The differences in samples of matched pairs Sample-1– Sample-2 is,
| S.no | Sample-1 | Sample-2 | |
| 1 | 28 | 34 | |
| 2 | 29 | 30 | |
| 3 | 22 | 31 | |
| 4 | 25 | 26 | |
| 5 | 26 | 31 | |
| 6 | 29 | 30 | |
| 7 | 27 | 31 | |
| 8 | 24 | 32 | |
| 9 | 27 | 29 | |
| 10 | 28 | 37 |
b.
Find the value of t-test statistic.
b.
Answer to Problem 10E
The value of test statistic is –4.3948.
Explanation of Solution
Calculation:
The test hypotheses are given below:
Null hypothesis:
That is, there is no significant difference between the population mean1 and population mean2.
Alternate hypothesis:
That is, there is a significant difference between the population mean1 and population mean2.
Mean and standard deviation of differences:
Software procedure:
Step-by-step procedure to obtain the mean and standard deviation using the MINITAB software:
- Choose Stat > Basic statistic > Display
descriptive statistics . - In Variables, enter the column of Differences.
- In Statistics, select mean, standard deviation and N total.
- Click OK.
Output using the MINITAB software is given below:
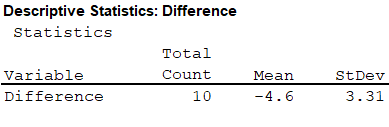
From the MINITAB output, the mean and standard deviation are –4.6 and 3.31.
The mean and standard deviation of the differences is –4.6 and 3.31.
The test statistic is obtained as follows,
Thus, the test statistic is –4.3948.
c.
Check whether the null hypothesis is rejected at
c.
Answer to Problem 10E
There is enough evidence to reject the null hypothesis
Explanation of Solution
Degrees of freedom:
The degrees of freedom for the test statistic is,
Thus, the degree of freedom is 9.
P-value:
Software procedure:
Step-by-step procedure to obtain the P-value using the MINITAB software:
- Choose Graph > Probability Distribution Plot.
- Choose View Probability > OK.
- From Distribution, choose ‘t’ distribution.
- In Degrees of freedom, enter 9.
- Click the Shaded Area tab.
- Choose X value and Both Tail for the region of the curve to shade.
- In X-value enter –4.3948.
- Click OK.
Output using the MINITAB software is given below:
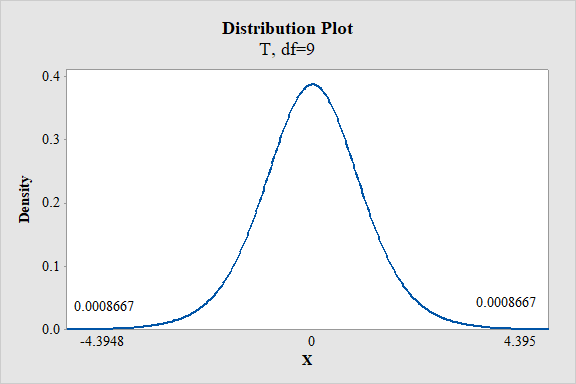
From the MINITAB output, the P-value is
Thus, the P-value is 0.0017.
Decision rule based on P-value:
If
If
Here, the level of significance is
Conclusion based on P-value approach:
The P-value is 0.0017 and
Here, P-value is less than the
That is,
By the rejection rule, reject the null hypothesis.
Thus, there is enough evidence to reject the null hypothesis
d.
Check whether the null hypothesis is rejected at
d.
Answer to Problem 10E
There is enough evidence to reject the null hypothesis
Explanation of Solution
From part (c), the P-value is 0.0017.
Decision rule based on P-value:
If
If
Here, the level of significance is
Conclusion based on P-value approach:
The P-value is 0.0017 and
Here, P-value is less than the
That is,
By the rejection rule, reject the null hypothesis.
Thus, there is enough evidence to reject the null hypothesis
Want to see more full solutions like this?
Chapter 9 Solutions
ALEKS 360 ESSENT. STAT ACCESS CARD
- Business Discussarrow_forwardTriola statistics Readers who prefer printed books Readers who prefer e-booksarrow_forwardThe following is a list of data on the duration of a sample of 200 outbreaks, in hours. 107 73 68 97 76 79 94 59 98 57 54 65 71 70 84 88 62 82 61 79 98 66 62 79 86 68 74 61 62 116 65 88 64 79 78 74 92 75 5289 85 28 73 80 68 78 89 72 78 88 77 103 88 63 68 90 62 89 71 71 74 222 R 82 79 70 ST☑ 65 98 77 86 58 69 88 81 74 70 65 81 75 81 78 90 78 96 75 KRRE F S 62 94 62 79 83 93 135 71 85 84 83 63 61 65 83 70 70 81 77 72 84 33 62 92 65 67 59 58 66 66 94 77 63 71 101 78 43 78 66 75 68 76 59 67 61 71 64 76 72 77 74 65 82 86 66 86 68 85 27% 96 72 77 60 67 87 83 68 72 74 91 76 83 งงง 8 སྐྱ ཐྭ ༄ ཏྱཾ 89 81 71 85 99 59 92 87 84 75 77 51 45 80 84 93 69 76 89 75 67 92 89 82 96 77 102 66 68 61 73 72 76 73 77 79 94 63 59 62 71 81 65 73 63 63 89 82 64 85 92 64 73 a. What is the variable? What type? b. Construct an interval-frequency table, with columns containing: class mark, absolute frequency, relative frequency, cumulative frequency, cumulative relative frequency, and percentage frequency.arrow_forward
- This is the information about the actors who won the Best Actor Oscar: Best actors 44 41 62 52 41 34 34 52 41 37 38 34 32 40 43 56 41 39 49 57 35 30 39 41 44 41 38 42 52 51 49 35 47 31 47 37 57 42 45 42 44 62 43 42 48 49 56 38 60 30 40 42 36 76 39 53 45 36 62 43 51 32 42 54 52 37 38 32 45 60 46 40 36 47 29 43 a. What is the variable? What type? b. Construct an interval-frequency table, with columns containing: class mark, absolute frequency, relative frequency, cumulative frequency, cumulative relative frequency, and percentage frequency.arrow_forwardans c plsarrow_forwardCritically analyze the following graph and, based on statistical information, indicate the type of error it presents IN NO MORE THAN 3 LINES SCOTCEN POLL OF POLLS SHOULD SCOTLAND BE INDEPENDENT? NO 52% YES 58% LIVE CAW NAS & 28.30 HAS KILLED MORE THAN 2,600 IN WEST AFRICA, WORLD HEALTH ORG. BROOKEBCNNarrow_forward
- Critically analyze the following graph and, based on statistical information, indicate the type of error it presents IN NO MORE THAN 3 LINES PRESIDENTIAL PREFERENCES RODOLFO CARTER 3% (+2pts) EVELYN MATTHEI 22% (+6pts) With the exception of President Boric, could you tell me who you would like to be the next president of Chile? CAMILA VALLEJO 4% (+2pts) JOSÉ ANTONIO KAST 19% (+5pts) MICHELLE BACHELET 6% (+1pts)arrow_forwardCritically analyze the following graph and, based on statistical information, indicate the type of error it presents IN NO MORE THAN 3 LINES 13% APPROVE 4% DOESN'T KNOW DOESN'T RESPOND 5% NEITHER APPROVES NOR DISAPPROVES 78% DISAPPROVES SURVEY PRESIDENTIAL APPROVAL DROPS TO 13%arrow_forwardPlease help with this following question I'm not too sure if question (a) and (b) are correct and not sure how to calculate (c) The csv data is below "","New","Current" "1","67",66 "2","77",73 "3","76",73 "4","76",76 "5","77",79 "6","84",76 "7","71",78 "8","84",72 "9","73",76 "10","71",73 "11","72",77 "12","70",72 "13","75",72 "14","84",71 "15","77",73 "16","65",72 "17","69",73 "18","71",73 "19","79",71 "20","75",78 "21","76",69 "22","73",74 "23","76",71 "24","64",74 "25","81",78 "26","79",76 "27","70",77 "28","79",71 "29","84",73 "30","79",69 "31","69",72 "32","81",76 "33","77",70 "34","77",71 "35","71",69 "36","67",72 "37","70",76 "38","77",73 "39","82",73 "40","72",73arrow_forward
- Please help me answer the following question(c) A previous study found that 15% of nurses reported participating in mental health support programs.From the 96% found in (b) , can you conclude that proportion of nurses reported participating in mental health support programs p(current), has changed from the previous study?(Yes/No) because the confidence interval in (b) (captures/does not capture) 15%.(d) Refer to your answer in (b) : The Alberta Nurses Association expects that not more than 23 % of nurses will participate in the survey on mental health support programs. Given the result in part (b) can we conclude that this expectation is reasonable?(Yes/No) because the (upper bound/lower bound) of the 96% confidence interval is (less than/not less than/greater than) 23%. The Alberta Nursing Association conducts an annual survey to estimate the proportion of nurses who participate in mental health support programs. The most recent application of this survey involved a random sample of…arrow_forwardPlease help me solve this questionThis is what was in the csv file:"","Diabetic","Heart Disease""1",32644,30646"2",789,1670"3",12802,36274"4",2177,5011"5",1910,3300"6",3320,4256"7",61425,39053"8",19768,28635"9",19502,39546"10",5642,12182"11",107864,152098"12",29918,60433"13",2397,3550"14",41559,34705"15",49169,57948"16",72853,83100"17",2155,2873"18",140220,134517"19",28181,26212"20",18850,38637"21",69564,68582"22",13897,12613"23",6868,9138"24",9735,4767"25",12102,13447"26",36571,50010"27",44665,55141"28",26620,33970"29",25525,29766"30",14167,20206Q(b) From this, the relationship between these two variables is (non-existent/positive/negative) . I can categorize this relationship as being (strong/weak/moderate).Q(c) Drop down is (+/-)Q(d) Drop downs in order are __% of the (average/median/variation/standard deviation) in the (the number of people diagnosed with heart disease/the number of people diagnosed with diabetes)−variable can be explained by its (linear relationship/relationship)…arrow_forwardPlease help me answer the following question The drop down for question (e, f, and g) is (YES/NO) Based on the P-value above, the assumption of equal variances among the four machines (Is Met/Is Not Met) Based on the data, the average fill for machine 3 is (statistically lower than/statistically higher than/the same as/not statistically different than/statistically different than/Hard to say then when comparing to/Refuse to say when comparing to) machine 1.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
