Chapter 9.1, Problem 63E

To determine

To Evaluate: Expression of river velocity in component form, expression of velocity of motorboat relative to water in component form, true velocity of motorboat as a vector and true speed and direction of motorboat.

Answer to Problem 63E

The expression of river velocity in component form is $10i$. Expression of velocity of motorboat in component form relative to water is $10i+10\sqrt{3}j$. True velocity of motorboat as a vector is $20i+10\sqrt{3}j$. True speed of jet is $26.45\text{mi/h}$ and direction of jet is $\text{N}49.1°\text{E}$.

Explanation of Solution

Given:

The speed of river is $10\text{mi/h}$ and river is flowing in east direction.

The speed of motorboat is $10\text{mi/h}$ and motorboat velocity makes $60°$ with the shore or positive $x$-axis.

The speed of river is $10\text{mi/h}$ and direction of wind is east. The speed of motorboat is $20\text{mi/h}$ and velocity of motorboat makes $60°$ with positive $x$-axis.

Formula used:

If velocity of river is vector u which makes angle $\theta$ with positive $x$ axis, then river velocity is

$u=\left|u\right|\cos \theta i+\left|u\right|\sin \theta j$ (1)

If velocity of motorboat is vector v which makes angle $\theta$ with positive $x$-axis, then  velocity of motorboat is,

$v=\left|v\right|\cos \theta i+\left|v\right|\sin \theta j$ (2)

If vector u is $u=a_{1}i+a_{2}j$ and vector v is $v=b_{1}i+b_{2}j$,

$u+v=\left(a_1+b_1\right)i+\left(a_2+b_2\right)j$ (3)

Calculation:

The speed of river is $10\text{mi/h}$ and direction of river is east.

The angle made by river velocity with positive $x$ axis is given by

$\theta =0°$

River velocity vector u is shown on coordinate axis in Figure (1).

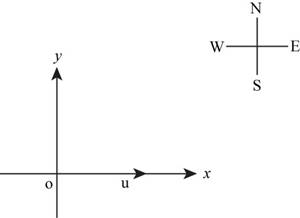
Figure (1)

Substitute $10$ for $\left|u\right|$, $0°$ for $\theta$ in equation (1).

$\begin{array}{c}v=10\cos 0°+10\sin 0°\\ =\left(10\times 1\right)i+\left(10\times 0\right)j\\ =10i\end{array}$

Thus, component form of river velocity u is $10i$.

Obtain the component form of motorboat velocity.

The speed of motorboat is $20\text{mi/h}$ and angle made by velocity of motorboat with positive $x$-axis is $60°$.

Velocity of motorboat is shown in Figure (2).

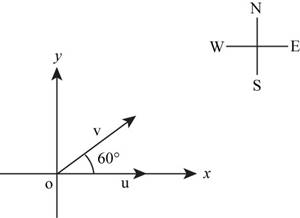
Figure (2)

Substitute $20$ for $\left|v\right|$, $60°$ for $\theta$ in equation (2).

$\begin{array}{c}v=20\cos 60°+20\sin 60°\\ =\left(20\times \frac{1}{2}\right)i+\left(20\times \frac{\sqrt{3}}{2}\right)j\\ =10i+10\sqrt{3}j\end{array}$

Thus, component form of motorboat velocity u is $10i+10\sqrt{3}j$.

Obtain the true velocity of motorboat.

If true velocity of motorboat is vector p , then vector p will be the resultant sum of river velocity u and velocity v of motorboat.

$p=u+v$

Figure (3) shows the vector u, vector v and vector p on coordinate axis.

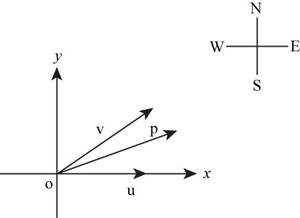
Figure (3)

From section(a) river velocity u is $10i$ and from section (b) velocity of motorboat v is $10i+10\sqrt{3}j$ and

Substitute $10$ for $a_1$, $0$ for $a_2$, $10$ for $b_1$ and $10\sqrt{3}$ for $b_2$ in equation (3).

$\begin{array}{c}u+v=\left(10+10\right)i+\left(0+10\sqrt{3}\right)j\\ =20i+10\sqrt{3}j\end{array}$

And vector p is $p=u+v$.

Therefore, $p=20i+10\sqrt{3}j$ .

Thus true velocity of motorboat is $20i+10\sqrt{3}j$.

From Section(c), the true velocity of motorboat is $20i+10\sqrt{3}j$.

Substitute $20$ for $a_1$ and $10\sqrt{3}$ for $a_2$ in equation (3).

$\begin{array}{l}\left|p\right|=\sqrt{{\left(20\right)}^2+{\left(10\sqrt{3}\right)}^2}\\ =\sqrt{400+300}\\ =\sqrt{700}\\ =26.45\end{array}$

Therefore, true speed of motorboat is $26.45\text{mi/h}$.

If ${\theta }_1$ is the angle made by true velocity vector p with the positive $x$ axis, then

angle ${\theta }_1$ has the property that,

$\tan {\theta }_1=\frac{\text{Vertical}\text{component}}{\text{Horizontal}\text{component}}$

From section (c), true velocity vector of motorboat is $20i+10\sqrt{3}j$.

Thus,

$\begin{array}{c}\tan {\theta }_1=\frac{10\sqrt{3}}{20}\\ =\frac{\sqrt{3}}{2}\end{array}$

Solve for ${\theta }_1$.

$\begin{array}{c}{\theta }_1={\tan }^{-1}\left(\frac{\sqrt{3}}{2}\right)\\ =49.1°\end{array}$

So, direction is $\text{N}49.1°\text{E}$.

Therefore true speed of motorboat is $26.45\text{mi/h}$ and direction is. $\text{N}49.1°\text{E}$.