
In Problems 8-12, please use the following steps (i)-(v) for all hypothesis tests:
(i) What is the level of significance? State the null and alternate hypotheses.
(ii) Check Requirements What sampling distribution will you use? What assumptions are you making? What is the value of the sample test statistic?
(iii) Find (or estimate) the P-value. Sketch the sampling distribution and show the area corresponding to the P-value.
(iv) Based on your answers in parts (i)-(iii), will you reject or fail to reject the null hypothesis? Are the data statistically significant at level a?
(v) Interpret your conclusion in the context of the application.
Note: For degrees of freedom d.f. not in the Student’s t table, use the closet d.f. that is smaller. In some situation, this choice of d.f. may increase the P-value a small amount and thereby produce a slightly more "conservative” answer.
Testing and Estimating µ with σ Unknown Carboxyhemoglobin is formed when hemoglobin is exposed to carbon monoxide. Heavy smokers tend to have a high percentage of carboxyhemoglobin in their blood (Reference: A Manual of Laboratory and Diagnostic Tests by F. Fischbach). Let x be a random variable representing percentage of carboxyhemoglobin in the blood. For a person who is a regular heavy smoker, x has a distribution that is approximately normal. A random sample of n = 12 blood tests given to a heavy smoker gave the following results (percentage of carboxyhemoglobin in the blood):
| 9.1 | 9.5 | 10.2 | 9.8 | 11.3 | 12.2 |
| 11.6 | 10.3 | 8.9 | 9.7 | 13.4 | 9.9 |
(a) Use a calculator to verify that
(b) A long-term population
(c) Use the given data to find a 99% confidence interval for µ for this patient.
(a)
Whether the sample mean
Answer to Problem 9CRP
Solution:
Yes, the sample mean
Explanation of Solution
To calculate the required statistics using the Minitab, follow the below instructions:
Step 1: Go to the Minitab software.
Step 2: Go to Stat >Basic statistics > Display Descriptive Statistics.
Step 3: Select ‘Percentages’ in variables.
Step 4: Click on OK.
The obtained statistics is:
Descriptive Statistics: Percentages
Statistics
| Variable | N | N* | Mean | SE Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum |
| Percentages | 12 | 0 | 10.492 | 0.392 | 1.358 | 8.900 | 9.550 | 10.050 | 11.525 | 13.400 |
From the Minitab output, the sample mean and sample standard deviation are approximately equals to
(b)
(i)
The level of significance, null and alternative hypothesis.
Answer to Problem 9CRP
Solution:
The level of significance is
Explanation of Solution
The level of significance is defined as the probability of rejecting the null hypothesis when it is true, it is denoted by
Null hypothesis
Alternative hypothesis
(ii)
To find:
The sampling distribution that should be used and compute the value of the sample test statistic.
Answer to Problem 9CRP
Solution:
The student's t distribution should be used. The sample test statisticis 1.25.
Explanation of Solution
Calculation:
We assume that x distribution is mound shape and symmetrical, because
Using
The sample test statistic t is
(iii)
To find:
The P-value of the test statistic and sketch the sampling distribution showing the area corresponding to the P-value.
Answer to Problem 9CRP
Solution:
The P-value of the test statistic is 0.1186.
Explanation of Solution
Calculation:
We have t = 1.25
Using Table 4 from the Appendix to find the specified area:
Graph:
To draw the required graphs using the Minitab, follow the below instructions:
Step 1: Go to the Minitab software.
Step 2: Go to Graph > Probability distribution plot > View probability.
Step 3: Select ‘t’ and enter d.f = 11.
Step 4: Click on the Shaded area > X value.
Step 5: Enter X-value as 1.25 and select ‘Right Tail’.
Step 6: Click on OK.
The obtained distribution graph is:
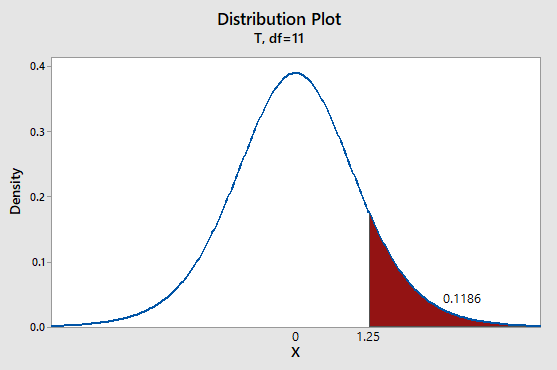
(iv)
Whether we reject or fail to reject the null hypothesisand whether the data is statistically significant for a level of significance of 0.05.
Answer to Problem 9CRP
Solution:
The P-value
Explanation of Solution
The P-value of 0.1186 is greater than the level of significance (α) of 0.05. Therefore we failed to reject the null hypothesis
(v)
The interpretation for the conclusion.
Answer to Problem 9CRP
Solution:
There is not enough evidence to conclude that sample mean of 12 smokers' Carboxyhoemoglobin levels is significantly large enough to sound a clinical alert.
Explanation of Solution
The P-value is greater than the level of significance (
(b)
To find:
A 99% confidence interval for the mean for this patient.
Answer to Problem 9CRP
Solution:
The 99% confidence interval for
Explanation of Solution
Calculation:
We have to find 99% confidence interval
Then, the 99% confidence interval is
The 99% confidence interval for
Want to see more full solutions like this?
Chapter 9 Solutions
Student Solutions Manual for Brase/Brase's Understanding Basic Statistics, 7th
- Consider an event X comprised of three outcomes whose probabilities are 9/18, 1/18,and 6/18. Compute the probability of the complement of the event. Question content area bottom Part 1 A.1/2 B.2/18 C.16/18 D.16/3arrow_forwardJohn and Mike were offered mints. What is the probability that at least John or Mike would respond favorably? (Hint: Use the classical definition.) Question content area bottom Part 1 A.1/2 B.3/4 C.1/8 D.3/8arrow_forwardThe details of the clock sales at a supermarket for the past 6 weeks are shown in the table below. The time series appears to be relatively stable, without trend, seasonal, or cyclical effects. The simple moving average value of k is set at 2. What is the simple moving average root mean square error? Round to two decimal places. Week Units sold 1 88 2 44 3 54 4 65 5 72 6 85 Question content area bottom Part 1 A. 207.13 B. 20.12 C. 14.39 D. 0.21arrow_forward
- The details of the clock sales at a supermarket for the past 6 weeks are shown in the table below. The time series appears to be relatively stable, without trend, seasonal, or cyclical effects. The simple moving average value of k is set at 2. If the smoothing constant is assumed to be 0.7, and setting F1 and F2=A1, what is the exponential smoothing sales forecast for week 7? Round to the nearest whole number. Week Units sold 1 88 2 44 3 54 4 65 5 72 6 85 Question content area bottom Part 1 A. 80 clocks B. 60 clocks C. 70 clocks D. 50 clocksarrow_forwardThe details of the clock sales at a supermarket for the past 6 weeks are shown in the table below. The time series appears to be relatively stable, without trend, seasonal, or cyclical effects. The simple moving average value of k is set at 2. Calculate the value of the simple moving average mean absolute percentage error. Round to two decimal places. Week Units sold 1 88 2 44 3 54 4 65 5 72 6 85 Part 1 A. 14.39 B. 25.56 C. 23.45 D. 20.90arrow_forwardThe accompanying data shows the fossil fuels production, fossil fuels consumption, and total energy consumption in quadrillions of BTUs of a certain region for the years 1986 to 2015. Complete parts a and b. Year Fossil Fuels Production Fossil Fuels Consumption Total Energy Consumption1949 28.748 29.002 31.9821950 32.563 31.632 34.6161951 35.792 34.008 36.9741952 34.977 33.800 36.7481953 35.349 34.826 37.6641954 33.764 33.877 36.6391955 37.364 37.410 40.2081956 39.771 38.888 41.7541957 40.133 38.926 41.7871958 37.216 38.717 41.6451959 39.045 40.550 43.4661960 39.869 42.137 45.0861961 40.307 42.758 45.7381962 41.732 44.681 47.8261963 44.037 46.509 49.6441964 45.789 48.543 51.8151965 47.235 50.577 54.0151966 50.035 53.514 57.0141967 52.597 55.127 58.9051968 54.306 58.502 62.4151969 56.286…arrow_forward
- The accompanying data shows the fossil fuels production, fossil fuels consumption, and total energy consumption in quadrillions of BTUs of a certain region for the years 1986 to 2015. Complete parts a and b. Year Fossil Fuels Production Fossil Fuels Consumption Total Energy Consumption1949 28.748 29.002 31.9821950 32.563 31.632 34.6161951 35.792 34.008 36.9741952 34.977 33.800 36.7481953 35.349 34.826 37.6641954 33.764 33.877 36.6391955 37.364 37.410 40.2081956 39.771 38.888 41.7541957 40.133 38.926 41.7871958 37.216 38.717 41.6451959 39.045 40.550 43.4661960 39.869 42.137 45.0861961 40.307 42.758 45.7381962 41.732 44.681 47.8261963 44.037 46.509 49.6441964 45.789 48.543 51.8151965 47.235 50.577 54.0151966 50.035 53.514 57.0141967 52.597 55.127 58.9051968 54.306 58.502 62.4151969 56.286…arrow_forwardThe accompanying data shows the fossil fuels production, fossil fuels consumption, and total energy consumption in quadrillions of BTUs of a certain region for the years 1986 to 2015. Complete parts a and b. Develop line charts for each variable and identify the characteristics of the time series (that is, random, stationary, trend, seasonal, or cyclical). What is the line chart for the variable Fossil Fuels Production?arrow_forwardThe accompanying data shows the fossil fuels production, fossil fuels consumption, and total energy consumption in quadrillions of BTUs of a certain region for the years 1986 to 2015. Complete parts a and b. Year Fossil Fuels Production Fossil Fuels Consumption Total Energy Consumption1949 28.748 29.002 31.9821950 32.563 31.632 34.6161951 35.792 34.008 36.9741952 34.977 33.800 36.7481953 35.349 34.826 37.6641954 33.764 33.877 36.6391955 37.364 37.410 40.2081956 39.771 38.888 41.7541957 40.133 38.926 41.7871958 37.216 38.717 41.6451959 39.045 40.550 43.4661960 39.869 42.137 45.0861961 40.307 42.758 45.7381962 41.732 44.681 47.8261963 44.037 46.509 49.6441964 45.789 48.543 51.8151965 47.235 50.577 54.0151966 50.035 53.514 57.0141967 52.597 55.127 58.9051968 54.306 58.502 62.4151969 56.286…arrow_forward
- For each of the time series, construct a line chart of the data and identify the characteristics of the time series (that is, random, stationary, trend, seasonal, or cyclical). Month PercentApr 1972 4.97May 1972 5.00Jun 1972 5.04Jul 1972 5.25Aug 1972 5.27Sep 1972 5.50Oct 1972 5.73Nov 1972 5.75Dec 1972 5.79Jan 1973 6.00Feb 1973 6.02Mar 1973 6.30Apr 1973 6.61May 1973 7.01Jun 1973 7.49Jul 1973 8.30Aug 1973 9.23Sep 1973 9.86Oct 1973 9.94Nov 1973 9.75Dec 1973 9.75Jan 1974 9.73Feb 1974 9.21Mar 1974 8.85Apr 1974 10.02May 1974 11.25Jun 1974 11.54Jul 1974 11.97Aug 1974 12.00Sep 1974 12.00Oct 1974 11.68Nov 1974 10.83Dec 1974 10.50Jan 1975 10.05Feb 1975 8.96Mar 1975 7.93Apr 1975 7.50May 1975 7.40Jun 1975 7.07Jul 1975 7.15Aug 1975 7.66Sep 1975 7.88Oct 1975 7.96Nov 1975 7.53Dec 1975 7.26Jan 1976 7.00Feb 1976 6.75Mar 1976 6.75Apr 1976 6.75May 1976…arrow_forwardHi, I need to make sure I have drafted a thorough analysis, so please answer the following questions. Based on the data in the attached image, develop a regression model to forecast the average sales of football magazines for each of the seven home games in the upcoming season (Year 10). That is, you should construct a single regression model and use it to estimate the average demand for the seven home games in Year 10. In addition to the variables provided, you may create new variables based on these variables or based on observations of your analysis. Be sure to provide a thorough analysis of your final model (residual diagnostics) and provide assessments of its accuracy. What insights are available based on your regression model?arrow_forwardI want to make sure that I included all possible variables and observations. There is a considerable amount of data in the images below, but not all of it may be useful for your purposes. Are there variables contained in the file that you would exclude from a forecast model to determine football magazine sales in Year 10? If so, why? Are there particular observations of football magazine sales from previous years that you would exclude from your forecasting model? If so, why?arrow_forward
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL



