
A simple beam ACE is constructed with square cross sections and a double taper (see figure). The depth of the beam at the supports is dAand at the midpoint is dc= 2d 4. Each half of the beam has length L. Thus, the depth and moment of inertia / at distance x from the left-hand end are, respectively, in which IAis the moment of inertia at end A of the beam. (These equations are valid for .x between 0 and L, that is, for the left-hand half of the beam.)
- Obtain equations for the slope and deflection of the left-hand half of the beam due to the uniform load.
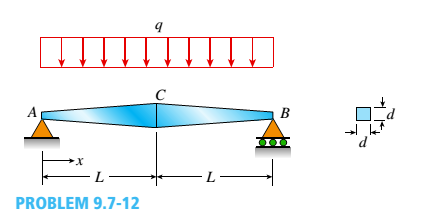
a.
The equations for the slope and deflection of the left-hand half of the beam for the given simple beam due to uniform load.
Answer to Problem 9.7.12P
The equation for the slope and deflection of the left-hand half of the beam are:
Explanation of Solution
Given: .
We have,
Length of the beam, AB =2L..
Depth of the beam at support,
Depth of the beam at midpoint,
Moment of inertia, I
Depth at the left-hand end,
Concept Used: .
Annuity problem requires the use of the differential equation as follows:.
Calculation: .
With the use of we can calculate,
The reaction forces at point A and B would be,
The bending moment would be,
Now we are using second degree differential eqaution as follow,
In the above equation taking integration at both sides,
The boundary conditions at x =L..
In the above equation, Once again taking integration, we will get,
Conclusion: .
The balance in the annuity after
b.
The formulas for the angle of rotation at the support and the deflection at the midpoint with the use of equations found in part (a).
Answer to Problem 9.7.12P
The equation for the angle of rotation
Explanation of Solution
Given: .
We have,
Length of the beam, AB =2L..
Depth of the beam at support,
Depth of the beam at midpoint,
Moment of inertia is I..
Depth at the left-hand end,
Concept Used: .
Annuity problem requires the use of the differential equation as follows:.
Calculation: .
We have the equation,
On this above equation, boundary condition at x =0 and v =0..
So, deflection beam would be,
Deflection at,
Conclusion: .
The equation for the angle of rotation
Want to see more full solutions like this?
Chapter 9 Solutions
Bundle: Mechanics Of Materials, Loose-leaf Version, 9th + Mindtap Engineering, 1 Term (6 Months) Printed Access Card
- I need help answering parts a and barrow_forwardRequired information Water initially at 200 kPa and 300°C is contained in a piston-cylinder device fitted with stops. The water is allowed to cool at constant pressure until it exists as a saturated vapor and the piston rests on the stops. Then the water continues to cool until the pressure is 100 kPa. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Water 200 kPa 300°C On the T-V diagram, sketch, with respect to the saturation lines, the process curves passing through the initial, intermediate, and final states of the water. Label the T, P, and V values for end states on the process curves. Please upload your response/solution by using the controls provided below.arrow_forwardA piston-cylinder device contains 0.87 kg of refrigerant-134a at -10°C. The piston that is free to move has a mass of 12 kg and a diameter of 25 cm. The local atmospheric pressure is 88 kPa. Now, heat is transferred to refrigerant-134a until the temperature is 15°C. Use data from the tables. R-134a -10°C Determine the change in the volume of the cylinder of the refrigerant-134a if the specific volume and enthalpy of R-134a at the initial state of 90.4 kPa and -10°C and at the final state of 90.4 kPa and 15°C are as follows: = 0.2418 m³/kg, h₁ = 247.77 kJ/kg 3 v2 = 0.2670 m³/kg, and h₂ = 268.18 kJ/kg The change in the volume of the cylinder is marrow_forward
- A piston-cylinder device contains 0.87 kg of refrigerant-134a at -10°C. The piston that is free to move has a mass of 12 kg and a diameter of 25 cm. The local atmospheric pressure is 88 kPa. Now, heat is transferred to refrigerant-134a until the temperature is 15°C. Use data from the tables. R-134a -10°C Determine the final pressure of the refrigerant-134a. The final pressure is kPa.arrow_forwardThe hydraulic cylinder BC exerts on member AB a force P directed along line BC. The force P must have a 560-N component perpendicular to member AB. A M 45° 30° C Determine the force component along line AB. The force component along line AB is N.arrow_forward! Required information A telephone cable is clamped at A to the pole AB. The tension in the left-hand portion of the cable is given to be T₁ = 815 lb. A 15° 25° B T₂ Using trigonometry, determine the required tension T₂ in the right-hand portion if the resultant R of the forces exerted by the cable at A is to be vertical. The required tension is lb.arrow_forward
- What are examples of at least three (3) applications of tolerance fitting analysis.arrow_forwardThe primary material used in the production of glass products is silica sand. True or Falsearrow_forwardWhich one of the following is the most common polymer type in fiber-reinforced polymer composites? thermosets thermoplastics elastomers none of the abovearrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
