Chapter 9, Problem 9.3.23P

-23 The beam shown in the figure has a sliding support at A and a roller support at B. The sliding support permits vertical movement but no rotation. Derive the equation of the deflection curve and determine the deflection ${\delta }_A$at end A and also ${\delta }_c$at point C due to the uniform load of intensity q = P/ L applied over segment CB and load P at x = L / 3. Use the second-order differential equation of the deflection curve.

To determine

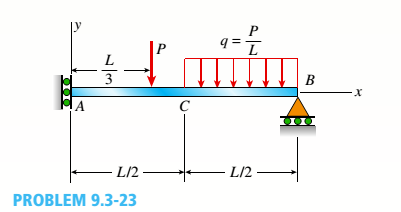
Derive the equations of the deflection curve and determine the deflection ${\delta }_A$ at end A and also ${\delta }_C$ at point C due to uniform load of intensity $q=\raisebox{1ex}{$P$}\!\left/ \!\raisebox{-1ex}{$L$}\right.$ applied over segment CB and load P at $x=\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ .

Answer to Problem 9.3.23P

Equations of deflection curve:

For $0\le x\le \frac{L}{3}$

  $v\left(x\right)=\frac{-PL}{10368EI}\left(-4104x^2+3565L^2\right)$

For $\frac{L}{3}\le x\le \frac{L}{2}$

  $v\left(x\right)=\frac{-P}{1152EI}\left(-648L{x}^2+192x^3+64L^{2}x+389L^3\right)$

For $\frac{L}{2}\le x\le L$

  $v\left(x\right)=\frac{-P}{144EI.L}\left(-72L^2{x}^2+12x^{3}L+6x^4+5L^{3}x+49L^4\right)$

Deflection at end A,

  ${\delta }_A=\frac{3565P{L}^3}{10368EI}$

Deflection at point C,

  ${\delta }_C=\frac{3109P{L}^3}{10368EI}$

Explanation of Solution

Given:

  

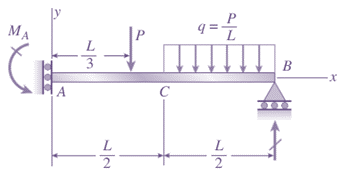
For $0\le x\le \frac{L}{3}$

  $EIv\text{'}\text{'}=M\left(x\right)=\frac{19}{24}PL$

  $EIv\text{'}=\frac{19}{24}PLx+C_1$

  $EIv=\frac{19}{48}PL{x}^2+C_{1}x+C_2$

B.C 1:

  $v\text{'}\left(0\right)=0$

Therefore,

  $C_1=0$

  $EIv\text{'}=\frac{19}{24}PLx$

  $EIv=\frac{19}{48}PL{x}^2+C_2$

For $\frac{L}{3}\le x\le \frac{L}{2}$

  $EIv\text{'}\text{'}=M\left(x\right)=\frac{19}{24}PL-P\left(x-\frac{L}{3}\right)$

  $EIv\text{'}\text{'}=M\left(x\right)=\frac{19}{24}PL-Px+\frac{PL}{3}$

  $EIv\text{'}=\frac{19}{24}PLx-\frac{P{x}^2}{2}+\frac{PLx}{3}+C_3$

  $EIv=\frac{19}{48}PL{x}^2-\frac{P{x}^3}{6}+\frac{PL{x}^2}{6}+C_{3}x+C_4$

For $\frac{L}{2}\le x\le L$

  $EIv\text{'}\text{'}=M\left(x\right)=\frac{19}{24}PL-Px+\frac{PL}{3}-\frac{P}{L}{\left(x-\frac{L}{2}\right)}^2\frac{1}{2}$

  $EIv\text{'}=\frac{19}{24}PLx-\frac{P{x}^2}{2}+\frac{PLx}{3}-\frac{P{x}^3}{6L}+\frac{P{x}^2}{4}-\frac{PLx}{8}+C_5$

  $EIv=\frac{19}{48}PL{x}^2-\frac{P{x}^3}{6}+\frac{PL{x}^2}{6}-\frac{P{x}^4}{24L}+\frac{P{x}^3}{12}-\frac{PL{x}^2}{16}+C_{5}x+C_6$

B.C 2:

  $v\left(L\right)=0$

Therefore,

  $0=\frac{19}{48}PL.L^2-\frac{P{L}^3}{6}+\frac{PL.L^2}{6}-\frac{P{L}^4}{24L}+\frac{P{L}^3}{12}-\frac{PL.L^2}{16}+C_{5}x+C_6$ .......(1)

B.C 3:

  $v{\text{'}}_L\left(\frac{L}{3}\right)=v{\text{'}}_R\left(\frac{L}{3}\right)$

Therefore,

  $0=-\frac{P{\left(\frac{L}{3}\right)}^2}{2}+\frac{PL{\left(\frac{L}{3}\right)}^2}{3}+C_3$ .......(2)

B.C 4:

  $v_L\left(\frac{L}{3}\right)=v_R\left(\frac{L}{3}\right)$

Therefore,

  $C_2=-\frac{P{\left(\frac{L}{3}\right)}^3}{6}+\frac{PL{\left(\frac{L}{3}\right)}^2}{6}+C_3\left(\frac{L}{3}\right)+C_4$.......(3)

B.C 5:

  $v{\text{'}}_L\left(\frac{L}{2}\right)=v{\text{'}}_R\left(\frac{L}{2}\right)$

Therefore,

  $C_3=-\frac{P{\left(\frac{L}{2}\right)}^3}{6L}+\frac{P{\left(\frac{L}{2}\right)}^2}{4}-\frac{PL\left(\frac{L}{2}\right)}{8}+C_5$ .......(4)

B.C 6:

  $v_L\left(a\right)=v_R\left(a\right)$

  $\frac{L}{2}{C}_3+C_4=-{\frac{P\left(\frac{L}{2}\right)}{24L}}^4+\frac{P{\left(\frac{L}{2}\right)}^3}{12}-\frac{PL{\left(\frac{L}{2}\right)}^2}{16}+C_5\left(\frac{L}{2}\right)+C_6$ .......(5)

From (1) − (5):

  $C_2=\frac{-3565}{10368}P{L}^3$

  $C_3=\frac{-1}{18}P{L}^2$

  $C_4=\frac{-389}{1152}P{L}^3$

  $C_5=\frac{-5}{144}P{L}^2$

  $C_6=\frac{-49}{144}P{L}^3$

For $0\le x\le \frac{L}{3}$

  $v\left(x\right)=\frac{-PL}{10368EI}\left(-4104x^2+3565L^2\right)$

For $\frac{L}{3}\le x\le \frac{L}{2}$

  $v\left(x\right)=\frac{-P}{1152EI}\left(-648L{x}^2+192x^3+64L^{2}x+389L^3\right)$

For $\frac{L}{2}\le x\le L$

  $v\left(x\right)=\frac{-P}{144EI.L}\left(-72L^2{x}^2+12x^{3}L+6x^4+5L^{3}x+49L^4\right)$

So,

  ${\delta }_A=-v\left(0\right)=\frac{3565P{L}^3}{10368EI}$

And

  ${\delta }_C=-v\left(\frac{L}{3}\right)=\frac{3109P{L}^3}{10368EI}$