Chapter 9, Problem 67SGR

To determine

To find: given table represents a linear or non linear equation.

$x$	$1$	$2$	$3$	$4$
$y$	$8$	$6$	$4$	$2$

Answer to Problem 67SGR

Given table illustrate a linear equation.

Explanation of Solution

Given:

$x$	$1$	$2$	$3$	$4$
$y$	$8$	$6$	$4$	$2$

Concept Used:

The slope intercept form equation is

  $y=mx+b$

Where;

Slope: $m$

Y-intercept: $\left(0,b\right)$

Calculation:

There are seven points are given as:

  $\begin{array}{l}A=\left(x_1,y_1\right)=\left(1,8\right)\\ B=\left(x_2,y_2\right)=\left(2,6\right)\\ C=\left(x_3,y_3\right)=\left(3,4\right)\\ D=\left(x_4,y_4\right)=\left(4,2\right)\end{array}$

Now use any two points to calculate the slope intercept from equation:

  $m=\frac{y_3-y_1}{x_3-x_1}=\frac{4-8}{3-1}=\frac{4}{2}=2$

Now, the slope intercept form equation is written as:

  $\begin{array}{l}y=mx+b\\ y=2x+b\end{array}$

Now put the value of $\left(x_1,y_1\right)=\left(1,8\right)$ in the above eq. to get the Y-intercept:

$\begin{array}{l}y=mx+b\\ 8=2\left(1\right)+b\\ b=8-2\\ b=6\end{array}$

So, the final slope intercept form equation is:

  $\begin{array}{l}y=mx+b\\ y=2x+6\end{array}$

The scatter plot and the line of fits are shown by the following graph by using the above data points and line of fit eq. or slope-intercept form eq.

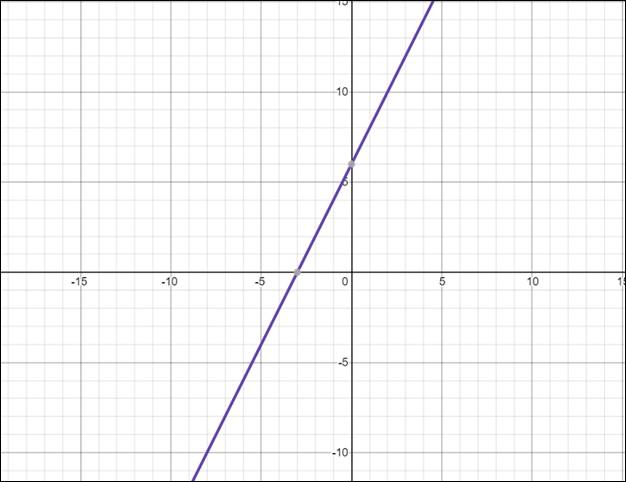
Conclusion:

Hence, with the help of slope-intercept form the line of fit is drawn and given table illustrate a linear equation.