
Concept explainers
A particle moves in the xy plane (Fig. P9.30) from the origin to a point having coordinates x = 7.00 m and y = 4.00 m under the influence of a force given by
- a. What is the work done on the particle by the force F if it moves along path 1 (shown in red)?
- b. What is the work done on the particle by the force F if it moves along path 2 (shown in blue)?
- c. What is the work done on the particle by the force F if it moves along path 3 (shown in green)?
- d. Is the force F conservative or nonconservative? Explain.
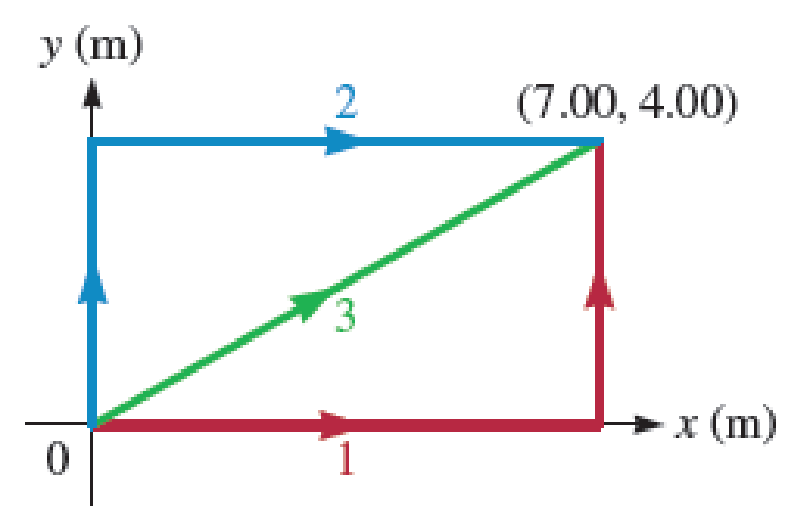
FIGURE P9.30
In each case, the work is found using the integral of
(a) The work done along path 1, we first need to integrate along
Performing the dot products, we get
Along the first part of this path, y = 0 therefore the first integral equals zero. For the second integral, x is constant and can be pulled out of the integral, and we can evaluate dy.
(b) The work done along path 2 is along
Performing the dot product, we get:
Along the first part of this path, x = 0. Therefore, the first integral equals zero. For the second integral, y is constant and can be pulled out of the integral, and we can evaluate dx.
(c) To find the work along the third path, we first write the expression for the work integral.
At first glance, this appears quite simple, but we can’t integrate
Now, use equation (2) in (1) to express each integral in terms of only one variable.
We can determine the tangent of the angle, which is constant (the angle is the angle of the line with respect to the horizontal).
Insert the value of the tangent and solve the integrals.
(d) Since the work done is not “path-independent”, this is
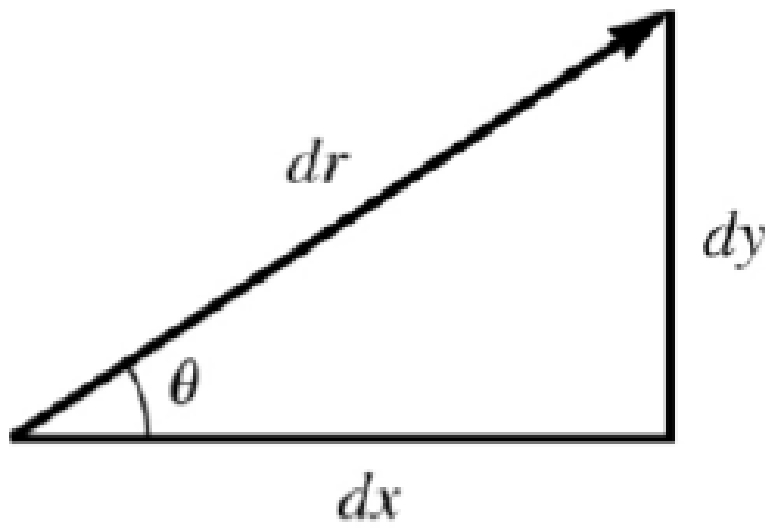
Figure P9.30ANS
(a)
The work done on the particle by the force
Answer to Problem 30PQ
The work done on the particle by the force
Explanation of Solution
The path 1 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is
Write the expression for the work done by a force.
Here,
The path 1 of the particle consist of two parts. Motion from
Use the force vector along with the limits of integration and perform the integration (represent the work done along path 1 as
Perform the dot product to reduce the integral (II).
Along the first part of the path 1,
Conclusion:
Therefore, the work done on the particle by the force
(b)
The work done on the particle by the force
Answer to Problem 30PQ
The work done on the particle by the force
Explanation of Solution
The path 2 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is
Equation (I) gives the expression for the work done by a force.
The path 2 of the particle consist of two parts. Motion from
Use the force vector along with the limits of integration and perform the integration (represent the work done along path 2 as
Perform the dot product to reduce the integral (IV).
Along the first part of the path 2,
Conclusion:
Therefore, the work done on the particle by the force
(c)
The work done on the particle by the force
Answer to Problem 30PQ
The work done on the particle by the force
Explanation of Solution
The path 3 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is
Equation (I) gives the expression for the work done by a force.
Write equation (I) in terms of
Use the
The path 3 of the particle starts from
Here, both
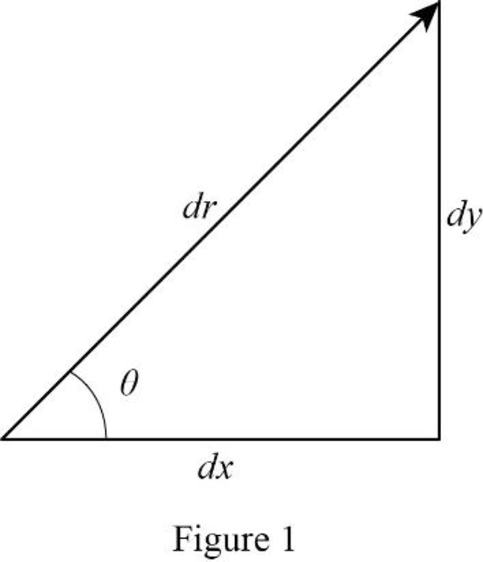
Write the expression relating
Solve equation (IX) for
Solve equation (IX) for
Use equation (X) and (XI) in (VIII).
Compute
Use equation (XIII) in (XII) and perform the integral.
Conclusion:
Therefore, the work done on the particle by the force
(d)
Whether the force
Answer to Problem 30PQ
The force
Explanation of Solution
From part (a), (b) and (c) it is found that the work done by the force
Conclusion:
Therefore, the force
Want to see more full solutions like this?
Chapter 9 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Consider 1 mole of supercooled water at -10°C. Calculate the entropy change of the water when the supercooled water freezes at -10°C and 1 atm. Useful data: Cp (ice) = 38 J mol-1 K-1 Cp (water) 75J mol −1 K -1 Afus H (0°C) 6026 J mol −1 Assume Cp (ice) and Cp (water) to be independent of temperature.arrow_forwardThe molar enthalpy of vaporization of benzene at its normal boiling point (80.09°C) is 30.72 kJ/mol. Assuming that AvapH and AvapS stay constant at their values at 80.09°C, calculate the value of AvapG at 75.0°C, 80.09°C, and 85.0°C. Hint: Remember that the liquid and vapor phases will be in equilibrium at the normal boiling point.arrow_forward3. The entropy of an ideal gas is S = Nkg In V. Entropy is a state function rather than a path function, and in this problem, you will show an example of the entropy change for an ideal gas being the same when you go between the same two states by two different pathways. A. Express ASV = S2 (V2) - S₁(V1), the change in entropy upon changing the volume from V₁to V2, at fixed particle number N and energy, U. B. Express ASN = S₂(N₂) - S₁ (N₁), the change in entropy upon changing the particle number from N₁ to N2, at fixed volume V and energy U. C. Write an expression for the entropy change, AS, for a two-step process (V₁, N₁) → (V2, N₁) → (V2, N₂) in which the volume changes first at fixed particle number, then the particle number changes at fixed volume. Again, assume energy is constant.arrow_forward
- Please don't use Chatgpt will upvote and give handwritten solutionarrow_forward6. We used the constant volume heat capacity, Cv, when we talked about thermodynamic cycles. It acts as a proportionality constant between energy and temperature: dU = C₁dT. You can also define a heat capacity for constant pressure processes, Cp. You can think of enthalpy playing a similar role to energy, but for constant pressure processes δαρ C = (37) - Sup Ср ат P = ат Starting from the definition of enthalpy, H = U + PV, find the relationship between Cy and Cp for an ideal gas.arrow_forwardPure membranes of dipalmitoyl lecithin phospholipids are models of biological membranes. They melt = 41°C. Reversible melting experiments indicate that at Tm AHm=37.7 kJ mol-1. Calculate: A. The entropy of melting, ASm- B. The Gibbs free energy of melting, AGm- C. Does the membrane become more or less ordered upon melting? D. There are 32 rotatable CH2 CH2 bonds in each molecule that can rotate more freely if the membrane melts. What is the increase in multiplicity on melting a mole of bonds?arrow_forward
- 5. Heat capacity often has a temperature dependence for real molecules, particularly if you go over a large temperature range. The heat capacity for liquid n-butane can be fit to the equation Cp(T) = a + bT where a = 100 J K₁₁ mol¹ and b = 0.1067 J K² mol¹ from its freezing point (T = 140 K) to its boiling point (T₁ = 270 K). A. Compute AH for heating butane from 170 K to 270 K. B. Compute AS for the same temperature range.arrow_forward4. How much energy must be transferred as heat to cause the quasi-static isothermal expansion of one mole of an ideal gas at 300 K from PA = 1 bar to PB = 0.5 bar? A. What is VA? B. What is VB? C. What is AU for the process? D. What is AH for the process? E. What is AS for the process?arrow_forward1. The diagram shows the tube used in the Thomson experiment. a. State the KE of the electrons. b. Draw the path of the electron beam in the gravitational field of the earth. C. If the electric field directed upwards, deduce the direction of the magnetic field so it would be possible to balance the forces. electron gun 1KVarrow_forward
- as a hiker in glacier national park, you need to keep the bears from getting at your food supply. You find a campground that is near an outcropping of ice. Part of the outcropping forms a feta=51.5* slopeup that leads to a verticle cliff. You decide that this is an idea place to hang your food supply out of bear reach. You put all of your food into a burlap sack, tie a rope to the sack, and then tie a bag full of rocks to the other end of the rope to act as an anchor. You currently have 18.5 kg of food left for the rest of your trip, so you put 18.5 kg of rocks in the anchor bag to balance it out. what happens when you lower the food bag over the edge and let go of the anchor bag? Determine the acceleration magnitude a of the two-bag system when you let go of the anchor bag?arrow_forward2. A thin Nichrome wire is used in an experiment to test Ohm's law using a power supply ranging from 0 to 12 V in steps of 2 V. Why isn't the graph of I vs V linear? 1. Nichrome wire does obey Ohm's law. Explain how that can that be true given the results abovearrow_forward1. The average KE and temperature in Kelvin of the molecules of a gas are related by the equation KE = 3/2 KT where k is the Boltzmann constant 1.38 x 10 m² kg s². The diagram shows the energy levels for a Hydrogen atom. Energy/eV 0.00 -1.51 3.39 13.58 Use this information to show that Hydrogen at room temperature will not emit light. 2. When hydrogen burns in oxygen 241.8 kJ of energy are released per mole. Show that this reaction can produce light.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





