Chapter 9, Problem 26E

For the circuit of Fig. 9.45, i_s(t) = 30u(−t) mA. (a) Select R₁ so that v(0⁺) = 6 V. (b) Compute v(2 ms). (c) Determine the settling time of the capacitor voltage. (d) Is the inductor current settling time the same as your answer to part (c)?

FIGURE 9.45

To determine

Select $R_1$ so that $v\left(0^{+}\right)=6\text{ V}$.

Answer to Problem 26E

The resistance $R_1$ is $5.128\Omega$.

Explanation of Solution

Given Data:

Formula used:

The expression for the exponential damping coefficient or the neper frequency is as follows:

$\alpha =\frac{1}{2RC}$ (1)

Here,

$\alpha$ is the exponential damping coefficient or the neper frequency,

$R$ is the resistance of a parallel $RLC$ circuit,

$C$ is the capacitance of a parallel $RLC$ circuit.

The expression for the resonant frequency is as follows:

${\omega }_0=\frac{1}{\sqrt{LC}}$ (2)

Here,

${\omega }_0$ is the resonant frequency and

$L$ is the inductance of a parallel $RLC$ circuit.

The expression for a critically damped response of a source free parallel RLC circuit is as follows:

$v\left(t\right)=\left(A_{1}t+A_2\right)e^{-\alpha t}\text{ V}$ (3)

Here,

$v\left(t\right)$ is the critically damped response of the parallel $RLC$ circuit,

$A_1$ and $A_2$ are arbitrary constants and

$t$ is the time.

Calculation:

The unit-step forcing function as a function of time which is zero for all values of its argument less than zero and which is unity for all positive values of its argument.

$u\left(t-t_0\right)=\{\begin{array}{l}0t<t_0\\ 1t>t_0\end{array}$

Here,

$t_0$ is the time at which the argument of the function becomes zero.

So, at $t=0^{-}$ the $30u\left(-t\right)\text{mA}$ independent current source is equal to $30\text{ mA}$.

The redrawn circuit diagram is given in Figure 1 at $t=0^{-}$.

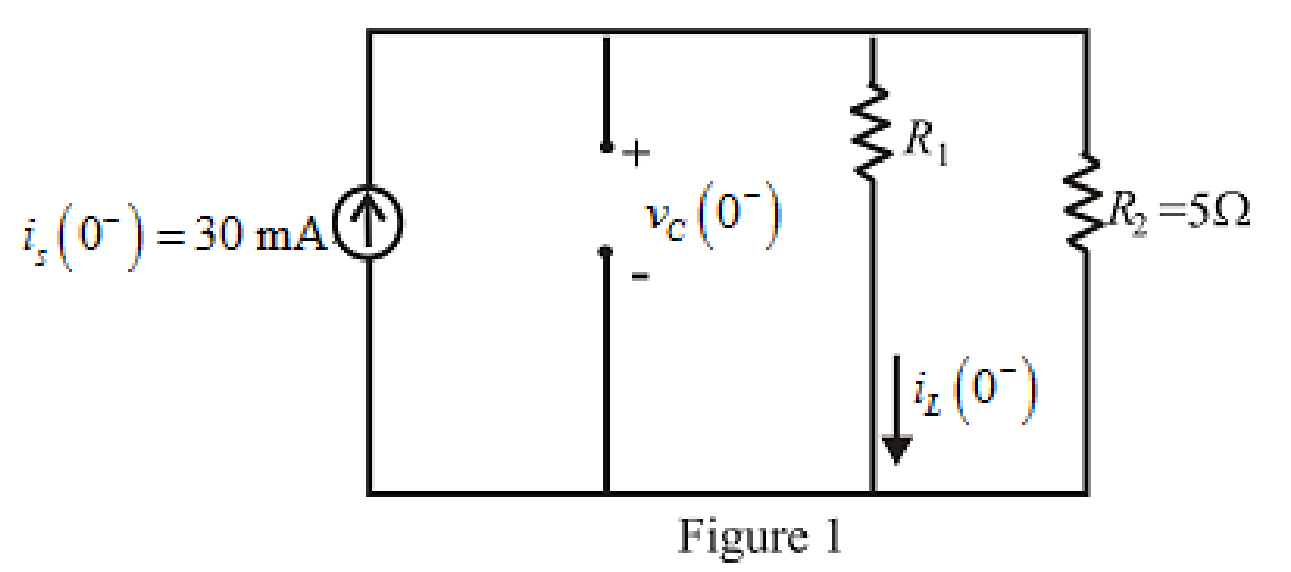
Refer to the redrawn Figure 1:

The expression for the current through the inductor at $t=0^{-}$ is as follows:

$i_L\left(0^{-}\right)=i_S\left(0^{-}\right)\left(\frac{R_2}{R_1+R_2}\right)$ (4)

Here,

$i_L\left(0^{-}\right)$ is the current through the inductor at $t=0^{-}$

$i_S\left(0^{-}\right)$ is the current through the $30u\left(-t\right)\text{mA}$ independent current source at $t=0^{-}$,

$R_1$ is the unknown resistor and

$R_2$ is the resistance of $5\Omega$ resistor.

The expression for the voltage across the capacitor at $t=0^{-}$ is as follows:

$v\left(0^{-}\right)=i_S\left(0^{-}\right)\left(\frac{R_2}{R_1+R_2}\right)R_1$ (5)

Here,

$v\left(0^{-}\right)$ is the voltage across the capacitor at $t=0^{-}$.

Substitute $30\text{ mA}$ for $i_S\left(0^{-}\right)$ and $5\Omega$ for $R_2$ in equation (5).

$v_C\left(0^{-}\right)=\left(30\text{ mA}\right)\left(\frac{5\Omega }{R_1+5\Omega }\right)R_1$ (6)

The capacitor does not allow sudden change in the voltage, so,

$v\left(0^{+}\right)=v\left(0^{-}\right)$ (7)

The voltage across the capacitor at $t=0^{+}$ is $\text{6 V}$.

Substitute $\text{6 V}$ for $v\left(0^{+}\right)$  and $\left(30\text{ mA}\right)\left(\frac{5\Omega }{R_1+5\Omega }\right)R_1$ for $v_C\left(0^{-}\right)$ in equation (7).

$\begin{array}{l}\text{6 V}=\left(30\text{ mA}\right)\left(\frac{5\Omega }{R_1+5\Omega }\right)R_1\\ \text{6 V}=\left(30\times {10}^{-3}\text{ A}\right)\left(\frac{5\Omega }{R_1+5\Omega }\right)R_1\left\{\because 1\text{ mA}={10}^{-3}\text{ A}\right\}\end{array}$

Rearrange for $R_2$.

$\begin{array}{l}\frac{\text{6 V}}{30\times {10}^{-3}\text{ A}}=\left(\frac{5\Omega }{R_1+5\Omega }\right)R_1\\ 200\left(R_1+5\Omega \right)=5R_1\\ 200R_1+1000\Omega +5R_1\\ 195R_1=-1000\Omega \end{array}$

$\begin{array}{c}{R}_1=\frac{-1000}{195}\Omega \\ =-5.128\Omega \end{array}$

The resistance cannot be negative so, the resistance $R_1$ is $5.128\Omega$.

Conclusion:

Thus, the resistance $R_1$ is $5.128\Omega$.

To determine

Compute $v\left(2\text{ ms}\right)$.

Answer to Problem 26E

The value of the voltage $v\left(2\text{ ms}\right)$ is $4.312\text{ V}$.

Explanation of Solution

Given data:

The time is $2\text{ ms}$.

Calculation:

Substitute $-5.128\Omega$ for $R_1$, $30\text{ mA}$ for $i_S\left(0^{-}\right)$ and $5\Omega$ for $R_2$ in equation (4).

$\begin{array}{c}{i}_L\left(0^{-}\right)=\left(30\text{ mA}\right)\left(\frac{5\Omega }{5.128\Omega +5\Omega }\right)\\ =\left(30\times {10}^{-3}\text{ A}\right)\left(\frac{5\Omega }{-5.128\Omega +5\Omega }\right)\left\{\because 1\text{ mA}={10}^{-3}\text{ A}\right\}\\ =\left(30\times {10}^{-3}\text{ A}\right)\left(-39.0625\right)\\ =-1.172\text{ A}\end{array}$

The inductor does not allow sudden change in the current.

So,

$i_L\left(0^{+}\right)=i_L\left(0^{-}\right)$

So the current through inductor at $t=0^{+}$ is $-1.172\text{ A}$.

The redrawn circuit diagram is given in Figure 2 at $t=0^{+}$.

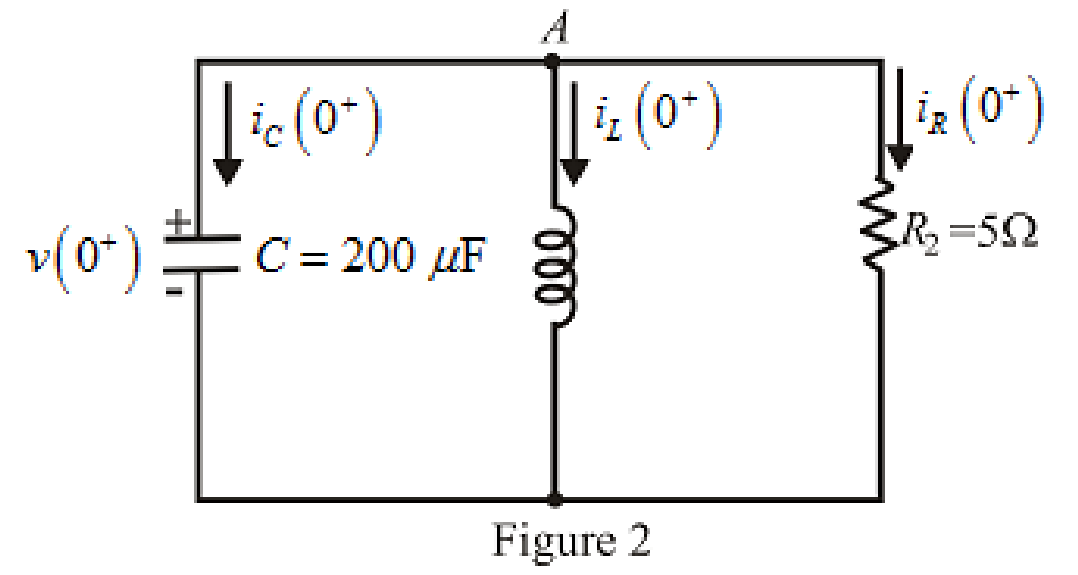
Refer to the redrawn Figure 2:

The expression for the current flowing in the $\text{5 }\Omega$ resistor at $t=0^{+}$ is as follows:

$i_R\left(0^{+}\right)=\frac{v_C\left(0^{+}\right)}{R_2}$ (8)

Here,

$i_R\left(0^{+}\right)$ is the current flowing in the $\text{5 }\Omega$ resistor at $t=0^{+}$.

Substitute $6\text{ V}$ for $v_C\left(0^{+}\right)$ and $\text{5 }\Omega$ for $R_2$ in equation (10).

$\begin{array}{c}{i}_R\left(0^{+}\right)=\frac{\text{6 V}}{\text{5 }\Omega }\\ =1.2\text{ A}\end{array}$

Apply KCL at node $A$.

$-i_C\left(0^{+}\right)+i_L\left(0^{+}\right)-i_R\left(0^{+}\right)=0\text{ A}$ (9)

Here,

$i_C\left(0^{+}\right)$ is the current flowing through $\text{200 }\mu \text{F}$ capacitor at $t=0^{+}$.

Substitute $-1.172\text{ A}$ for $i_L\left(0^{+}\right)$ and $1.2\text{ A}$ for $i_R\left(0^{+}\right)$ in equation (11).

$\begin{array}{l}-i_C\left(0^{+}\right)-\left(-1.172\text{ A}\right)-1.2\text{ A}=0\text{ A}\\ -i_C\left(0^{+}\right)+1.172\text{ A}-1.2\text{ A}=0\text{ A}\\ -i_C\left(0^{+}\right)-0.028\text{ A}=0\text{ A}\end{array}$

Rearrange for $i_C\left(0^{+}\right)$.

$i_C\left(0^{+}\right)=-0.028\text{ A}$

Substitute $\text{5 }\Omega$ for $R$ and $\text{200 }\mu \text{F}$ for $C$ in the equation (1).

$\begin{array}{c}\alpha =\frac{1}{2\left(\text{5 }\Omega \right)\left(\text{200 }\mu \text{F}\right)}\\ =\frac{1}{2\left(\text{5 }\Omega \right)\left(\text{200}\times {\text{10}}^{-6}\text{ F}\right)}\left\{\because 1\mu \text{F}={10}^{-6}\text{ F}\right\}\\ =500{\text{ s}}^{-1}\end{array}$

Substitute $\text{20 mH}$ for $L$ and $\text{200 }\mu \text{F}$ for $C$ in the equation (2).

$\begin{array}{c}{\omega }_0=\frac{1}{\sqrt{\left(\text{20 mH}\right)\times \left(\text{200 }\mu \text{F}\right)}}\\ =\frac{1}{\sqrt{\left(20\times {10}^{-3}\right)\times \left(\text{200}\times {\text{10}}^{-6}\text{ F}\right)}}\left\{\because 1\mu \text{F}={10}^{-6}\text{ F}\right\}\\ =500{\text{ s}}^{-1}\end{array}$

Substitute $500{\text{ s}}^{-1}$ for $\alpha$ in equation (6).

$v\left(t\right)=\left(A_{1}t+A_2\right)e^{-\left(500{\text{ s}}^{-1}\right)t}\text{ V}$ (10)

Substitute $0$ for $t$ in equation (10).

$\begin{array}{c}v\left(0\right)=\left(A_1\left(0\right)+A_2\right)e^{-\left(500{\text{ s}}^{-1}\right)\left(0\right)}\text{}\text{ V}\\ =A_2\left(1\right)\text{ V}\end{array}$

$v\left(0\right)=A_2\text{ V}$ (11)

The voltage across the capacitor at $t=0$ is $\text{6 V}$.

Substitute $\text{6 V}$ for $v\left(0\right)$ in equation (11).

$\text{6 V}=A_2\text{ V}$

Rearrange for $A_2$.

$A_2=6$ (12)

The expression for the current flowing through the $8\text{ nF}$ capacitor is as follows:

$i_C\left(t\right)=\frac{Cdv\left(t\right)}{dt}$ (13)

$v\left(t\right)$ is the voltage across the $8\text{ nF}$ capacitor for $t=0^{+}$.

Substitute $\left(A_{1}t+A_2\right)e^{-\alpha t}\text{ V}$ for $v\left(t\right)$ in equation (10).

$i_C\left(t\right)=\frac{Cd\left(\left(A_{1}t+A_2\right)e^{-\alpha t}\text{ V}\right)}{dt}$

Rearrange for $\frac{i_C\left(t\right)}{C}$.

$\frac{i_C\left(t\right)}{C}=\frac{d\left(\left(A_{1}t+A_2\right)e^{-\alpha t}\text{ V}\right)}{dt}$

$\frac{i_C\left(t\right)}{C}=\left(A_1{e}^{-\alpha t}-A_1\alpha t{e}^{-\alpha t}-\alpha e^{-\alpha t}{A}_2\right)\text{ V}$ (14)

Substitute $0$ for $t$ in equation (14).

$\begin{array}{c}\frac{i_C\left(0\right)}{C}=\left(A_1{e}^{-\alpha \left(0\right)}-A_1\alpha \left(0\right)e^{-\alpha \left(0\right)}-\alpha e^{-\alpha \left(0\right)}{A}_2\right)\text{ V}\\ =A_1\left(0\right)-0-\alpha \left(1\right)A_2\text{ V}\end{array}$

$\frac{i_C\left(0\right)}{C}=A_1-\alpha A_2\text{ V}$ (15)

The current flowing through the $\text{200 }\mu \text{F}$ capacitor at $t=0$ is $-0.028\text{ A}$.

Substitute $6$ for $A_2$ and $500{\text{ s}}^{-1}$ for $\alpha$ in equation (15).

$\frac{i_C\left(0\right)}{C}=A_1-\left(6\right)\left(500{\text{ s}}^{-1}\right)\text{ V}$

$\frac{i_C\left(0\right)}{C}=\left(A_1-3000{\text{ s}}^{-1}\right)\text{ V}$ (16)

Substitute $-0.028\text{ A}$ for $i_C\left(0\right)$ and $\text{200 }\mu \text{F}$ for $C$ in equation (16).

$\begin{array}{l}\frac{-0.028\text{ A}}{\text{200 }\mu \text{F}}=\left(A_1-3000{\text{ s}}^{-1}\right)\text{ V}\\ \frac{-0.028\text{ A}}{\text{200}\times {\text{10}}^{-6}\text{ F}}=\left(A_1-3000{\text{ s}}^{-1}\right)\text{ V }\left\{\because 1\mu \text{F}={10}^{-6}\text{ F}\right\}\\ -140\text{ V/s}=\left(A_1-3000{\text{ s}}^{-1}\right)\text{ V}\end{array}$

Rearrange for $A_1$.

$\begin{array}{l}{A}_1-3000{\text{ s}}^{-1}=-140{\text{ s}}^{-1}\\ A_1=2860{\text{ s}}^{-1}\end{array}$

Substitute $2860{\text{ s}}^{-1}$ for $A_1$ and $6$ for $A_2$ in equation (10).

$v\left(t\right)=\left(\left(2860{\text{ s}}^{-1}\right)t+\left(6\right)\right)e^{-\left(500{\text{ s}}^{-1}\right)t}\text{ V}$

$v\left(t\right)=\left(\left(2860{\text{ s}}^{-1}\right)t+6\right)e^{-\left(500{\text{ s}}^{-1}\right)t}\text{ V}$ (17)

Substitute $2\text{ ms}$ for $t$ in equation (17).

$\begin{array}{c}v\left(t\right)=\left(\left(2860{\text{ s}}^{-1}\right)\left(2\text{ ms}\right)+6\right)e^{-\left(500{\text{ s}}^{-1}\right)\left(2\text{ ms}\right)}\text{ V}\\ =\left(\left(2860{\text{ s}}^{-1}\right)\left(2\times {10}^{-3}\text{ s}\right)+6\right)e^{-\left(500{\text{ s}}^{-1}\right)\left(2\times {10}^{-3}\text{ s}\right)}\text{ V }\left\{\because 1\text{ ms}={10}^{-3}\text{ s}\right\}\\ =\left(5.72+6\right)e^{-\left(500{\text{ s}}^{-1}\right)\left(2\times {10}^{-3}\text{ s}\right)}\text{ V}\\ \text{=}\left(\text{11}\text{.72}\right)\left(0.36788\right)\text{ V}\end{array}$

$v\left(t\right)=4.312\text{ V}$

Conclusion:

Thus, the value of the voltage $v\left(2\text{ ms}\right)$ is $4.312\text{ V}$.

To determine

Determine the settling time of the capacitor voltage.

Answer to Problem 26E

The settling time of the capacitor voltage is $13.18\text{ s}$.

Explanation of Solution

Calculation:

The maximum voltage appears across the capacitor at $t=0$.

So, for maximum voltage,

Substitute $0$ for $t$ in equation (17).

$\begin{array}{c}v\left(0\right)=\left(\left(2860{\text{ s}}^{-1}\right)\left(0\right)+6\right)e^{-\left(500{\text{ s}}^{-1}\right)\left(0\right)}\text{ V}\\ =\left(\left(0\right)+6\right)\left(1\right)\text{ V}\\ =6\text{ V}\end{array}$

Settling time is the time at which the value of the voltage reaches $1\%$ of maximum value.

The expression for the voltage at $1\%$ of maximum value is as follows:

$v_{\text{ at }1\%}=v_{\text{ max}}\left(1\%\right)$ (18)

Here,

$v_{\text{ at }1\%}$ is the value of the voltage at $1\%$ of maximum value,

$v_{\text{ max}}$ the maximum voltage.

Substitute $6\text{ V}$ for $v_{\text{ max}}$ in equation (18).

$\begin{array}{c}{v}_{\text{ at }1\%}=6\text{ V}\left(1\%\right)\\ =6\text{ V}\left(\frac{1}{100}\right)\\ =0.06\text{ V}\end{array}$

Substitute $0.06\text{ V}$ for $v\left(t\right)$ in equation (17).

$0.06\text{ V}=\left(\left(2860{\text{ s}}^{-1}\right)t+6\right)e^{-\left(500{\text{ s}}^{-1}\right)t}\text{ V}$

$0.06=\left(\left(2860{\text{ s}}^{-1}\right)t+6\right)e^{-\left(500{\text{ s}}^{-1}\right)t}$

The value of $t$ is calculated by scientific calculator as,

$t=13.18\text{ s}$

Conclusion:

Thus, the settling time of the capacitor voltage is $13.18\text{ s}$.

To determine

Is the inductor current settling time the same as your answer to part (c)?

Answer to Problem 26E

The inductor current settling time is not same as capacitor voltage settling time.

Explanation of Solution

Calculation:

The expression for the current through inductor is as follows:

$i_L\left(t\right)=\frac{1}{L}{\displaystyle \int v\left(t\right)dt}$ (19)

Here,

$i_L\left(t\right)$ is the current through inductor.

Substitute $\left(\left(2860{\text{ s}}^{-1}\right)t+6\right)e^{-\left(500{\text{ s}}^{-1}\right)t}\text{ V}$ for $v\left(t\right)$ and $20\text{ mH}$ in equation (19).

$\begin{array}{c}{i}_L\left(t\right)=\frac{1}{20\text{ mH}}{\displaystyle \int \left(\left(2860{\text{ s}}^{-1}\right)t+6\right)e^{-\left(500{\text{ s}}^{-1}\right)t}dt\text{ V}}\\ =\frac{1}{20\times {10}^{-3}\text{ H}}{\displaystyle \int \left(\left(2860{\text{ s}}^{-1}\right)t+6\right)e^{-\left(500{\text{ s}}^{-1}\right)t}dt\text{ V}}\text{}\left\{\because 1\text{ mH}={10}^{-3}\text{ H}\right\}\\ \text{=50}{\displaystyle \int \left(2860t{e}^{-\left(500{\text{ s}}^{-1}\right)t}+6e^{-\left(500{\text{ s}}^{-1}\right)t}\right)dt\text{ V}}\\ ={\displaystyle \int \left(143000t{e}^{-\left(500{\text{ s}}^{-1}\right)t}+300e^{-\left(500{\text{ s}}^{-1}\right)t}\right)dt\text{ V}}\end{array}$

Simplify further.

$\begin{array}{c}{i}_L\left(t\right)=143000{\displaystyle \int t{e}^{-\left(500{\text{ s}}^{-1}\right)t}}dt+300{\displaystyle \int e^{-\left(500{\text{ s}}^{-1}\right)t}dt}\\ =143000\left(\frac{1}{500}{\displaystyle \int e^{-\left(500{\text{ s}}^{-1}\right)t}dt-\frac{t{e}^{-\left(500{\text{ s}}^{-1}\right)t}}{500}}\right)+300\left(-\frac{1}{500}{e}^{-\left(500{\text{ s}}^{-1}\right)t}\right)\\ =143000\left(\frac{1}{2500}{e}^{-\left(500{\text{ s}}^{-1}\right)t}-\frac{t{e}^{-\left(500{\text{ s}}^{-1}\right)t}}{500}\right)+300\left(-\frac{1}{500}{e}^{-\left(500{\text{ s}}^{-1}\right)t}\right)\\ =143000\left(-\frac{500t+1}{25000e^{-\left(500{\text{ s}}^{-1}\right)t}}\right)+300\left(-\frac{1}{500}{e}^{-\left(500{\text{ s}}^{-1}\right)t}\right)\end{array}$

$\begin{array}{c}{i}_L\left(t\right)=-0.573e^{-\left(500{\text{ s}}^{-1}\right)t}\left(500t+1\right)-0.6e^{-\left(500{\text{ s}}^{-1}\right)t}\\ =-e^{-\left(500{\text{ s}}^{-1}\right)t}\left(286.5t+0.573+0.6\right)\end{array}$

$i_L\left(t\right)=-e^{-\left(500{\text{ s}}^{-1}\right)t}\left(286.5t+1.173\right)\text{ A}$ (20)

The maximum current through the inductor is at $t=0$.

So, for the maximum current,

Substitute $0$ for $t$ in equation (20).

$\begin{array}{c}{i}_L\left(0\right)=-e^{-\left(500{\text{ s}}^{-1}\right)\left(0\right)}\left(\left(286.5\right)\left(0\right)+1.173\right)\text{ A}\\ =-\left(1\right)\left(\left(0\right)+1.173\right)\text{ A}\\ =-1.173\text{ A}\end{array}$

Settling time is the time at which the value of the current reaches $1\%$ of maximum value.

The expression for the current at $1\%$ of maximum value is as follows:

$i_{\text{ at }1\%}=i_{\text{ max}}\left(1\%\right)$ (21)

Here,

$i_{\text{ at }1\%}$ is the value of the current at $1\%$ of maximum value

$i_{\text{ max}}$ the maximum current.

Substitute $-1.173\text{ A}$ for $i_{\text{ max}}$ in equation (21).

$\begin{array}{c}{i}_{\text{ at }1\%}=-1.173\text{ A}\left(1\%\right)\\ =-1.173\text{ A}\left(\frac{1}{100}\right)\\ =-0.01173\text{ A}\end{array}$

Substitute $-0.01173\text{ A}$ for $i_L\left(t\right)$ in equation (20).

$-0.01173\text{ A}=-e^{-\left(500{\text{ s}}^{-1}\right)t}\left(286.5t+1.173\right)\text{ A}$ (22)

Rearrange equation (22).

$0.01173=e^{-\left(500{\text{ s}}^{-1}\right)t}\left(286.5t+1.173\right)$

The value of $t$ is calculated by scientific calculator.

$t=11.94\text{ s}$

So the inductor current settling time is $11.94\text{ s}$.

Conclusion:

Thus, the inductor current settling time is not same as capacitor settling time.