
Concept explainers
For the circuit represented by Fig. 9.44, the two resistor values are R1 = 0.752 Ω and R2 = 1.268 Ω, respectively. (a) Obtain an expression for the energy stored in the capacitor, valid for all t > 0; (b) determine the settling time of the current labeled iA.
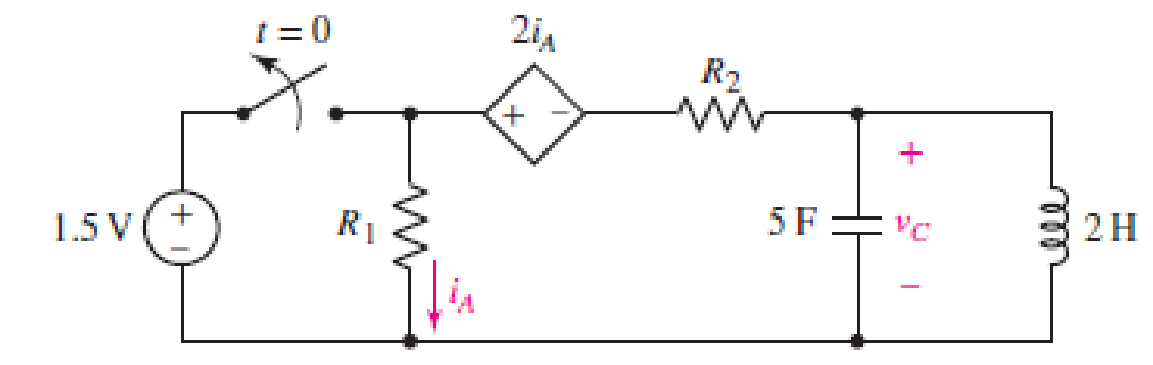
FIGURE 9.44
(a)
Find the expression for the energy stored in the capacitor, valid for all
Answer to Problem 20E
The expression for the energy stored in the capacitor, valid for all
Explanation of Solution
Given Data:
The value of the resistor
Formula used:
The expression for the exponential damping coefficient or the neper frequency is as follows:
Here,
The expression for the resonating frequency is as follows:
Here,
The expression for the two solutions of the characteristic equation of a parallel
Here,
The expression for the natural response of the parallel
Here,
The expression for the energy stored in the capacitor is as follows:
Here,
Calculation:
The capacitor and the inductor are connected in the circuit for long time.
So, the capacitor behaves as open circuit and the inductor behaves as short circuit.
The redrawn circuit diagram is given in Figure 1 for
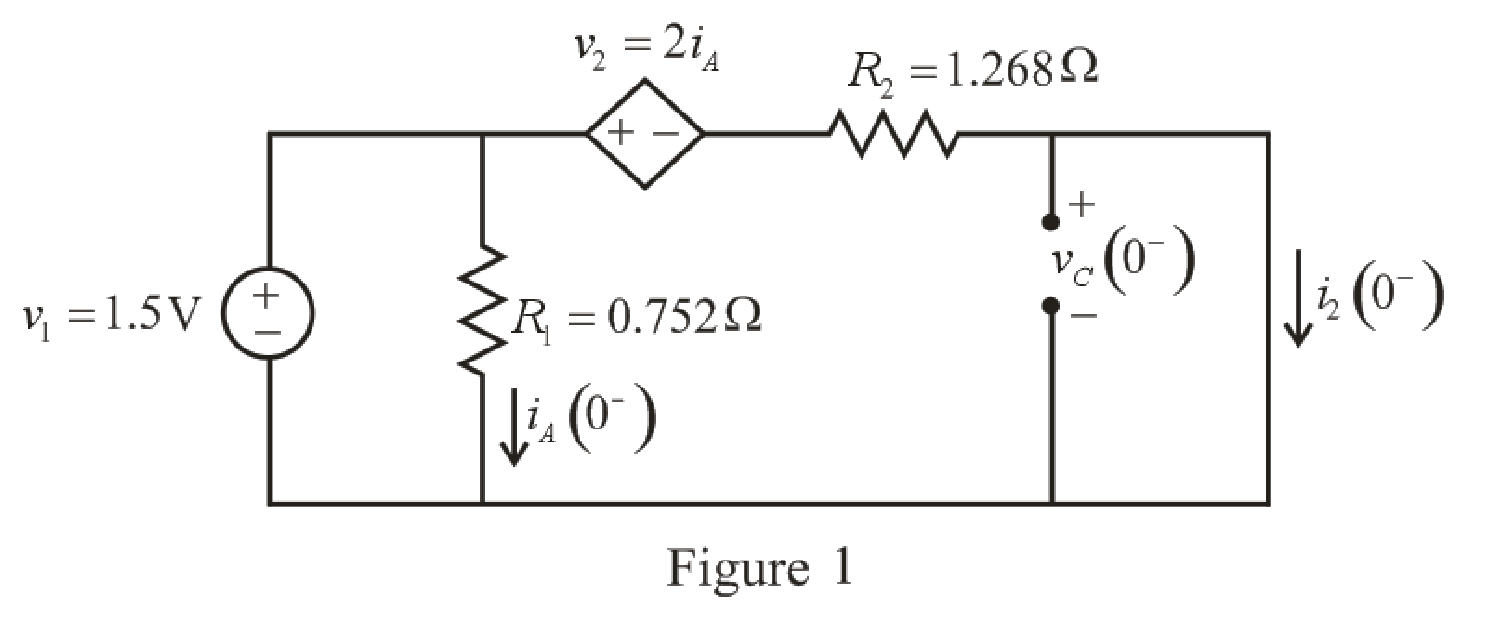
Refer to the redrawn Figure 1:
As parallel branches have same voltage so voltage across
The expression for the current flowing through
Here,
Substitute
The expression for the current flowing through the
Here,
Substitute
Substitute
As parallel branches have same voltage and the voltage across the short circuit branch has
The capacitor does not allow sudden change in the voltage and the inductor does not allow sudden change in current.
So,
Therefore, the voltage across the
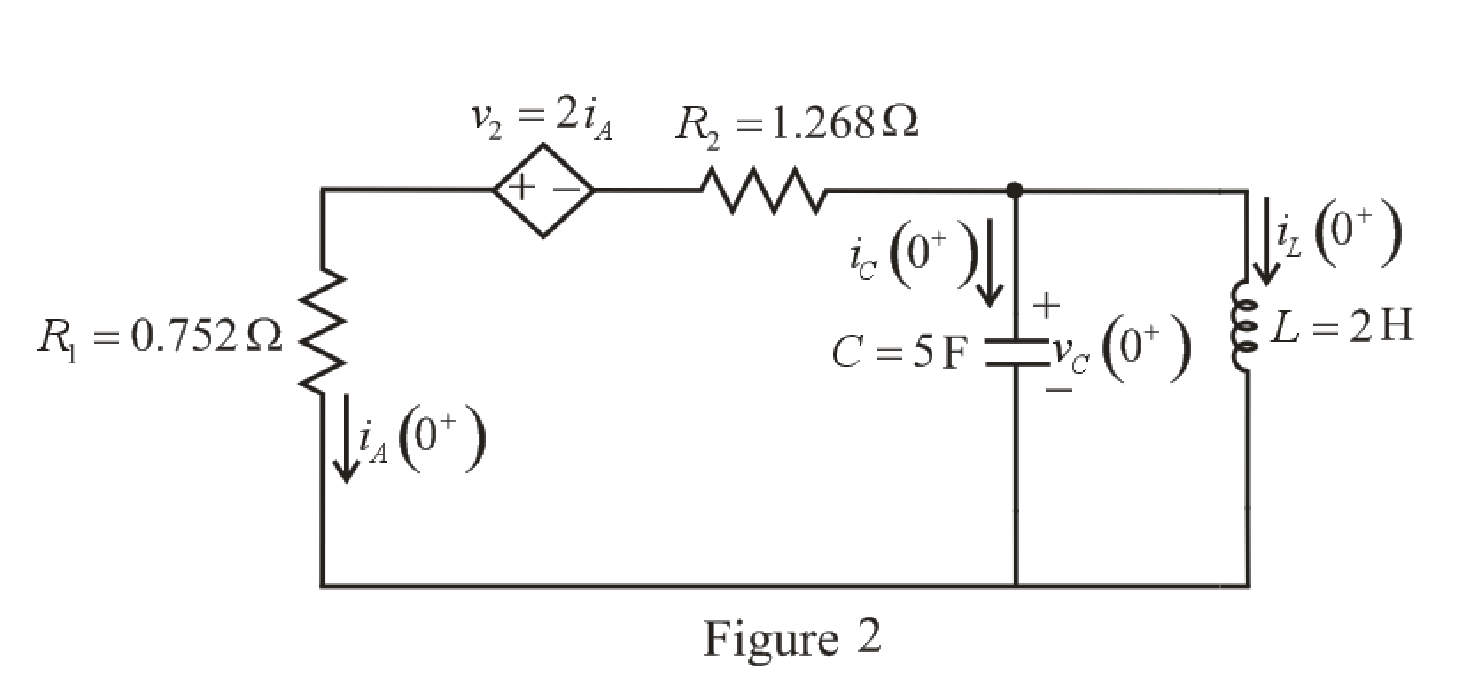
The redrawn circuit diagram is given in Figure 2 at
 l
l
Refer to the redrawn Figure 2:
As the voltage across the he
To find equivalent resistance across the capacitor, a
The redrawn circuit diagram is given in Figure 3.
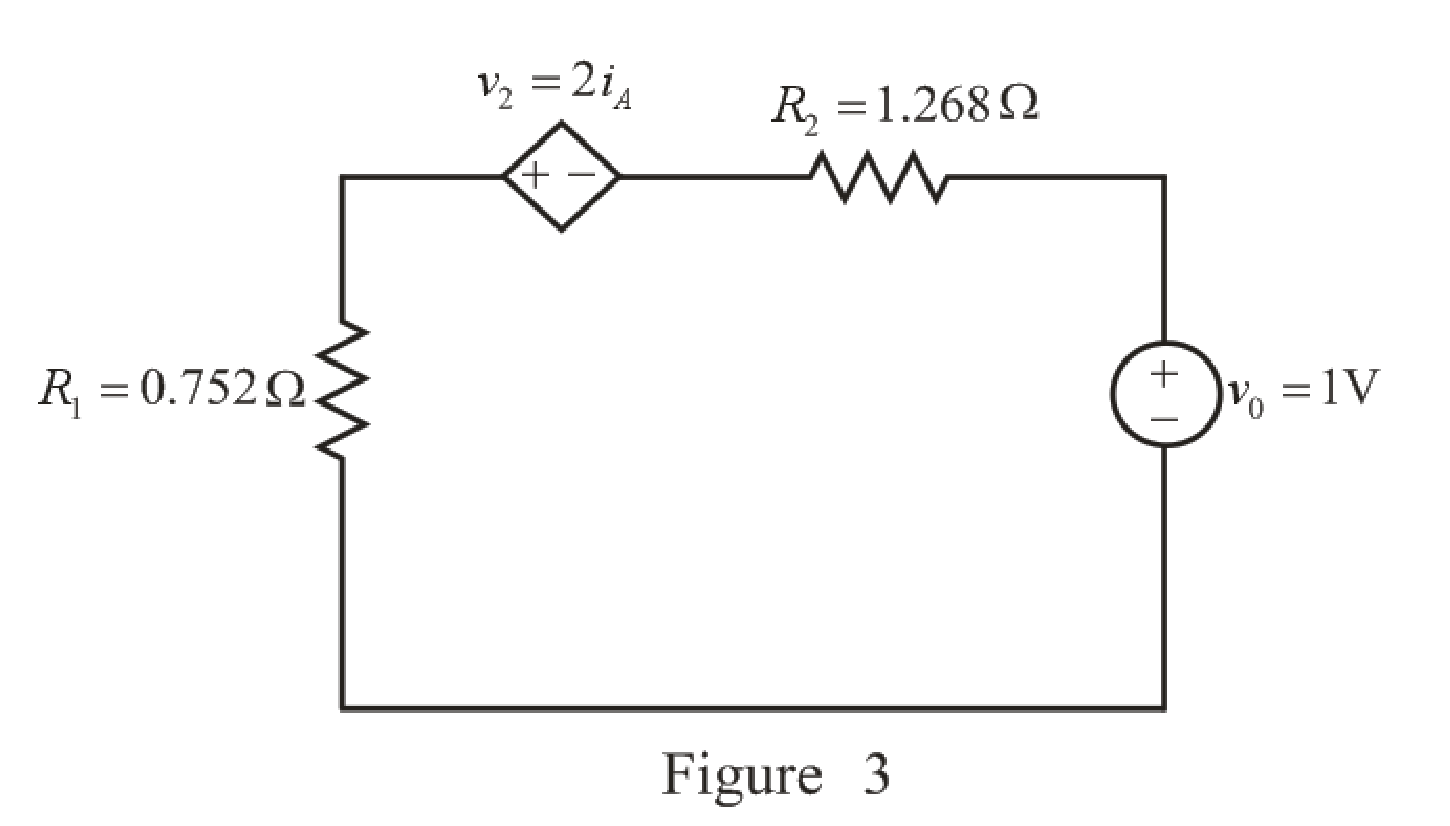
Refer to the redrawn Figure 3:
Apply KVL in the circuit.
Here,
Substitute
Rearrange for
The expression for the equivalent resistance the circuit is as follows:
Here,
Substitute
Substitute
Substitute
Here, the exponential damping coefficient is greater than the resonating frequency,
So, the response of the parallel
Substitute
Substitute
Substitute
Substitute
The voltage across the capacitor at
Substitute
Rearrange for
The expression for the current flowing through the
Substitute
Rearrange for
Substitute
The current flowing through the
Substitute
Rearrange for
Substitute
Rearrange for
Substitute
Substitute
Substitute
So, the energy stored in the capacitor, valid for all
Conclusion:
Thus, the expression for the energy stored in the capacitor, valid for all
(b)
Find the settling time of the current
Answer to Problem 20E
The settling time of current
Explanation of Solution
Calculation:
The redrawn circuit diagram is given in Figure 4.
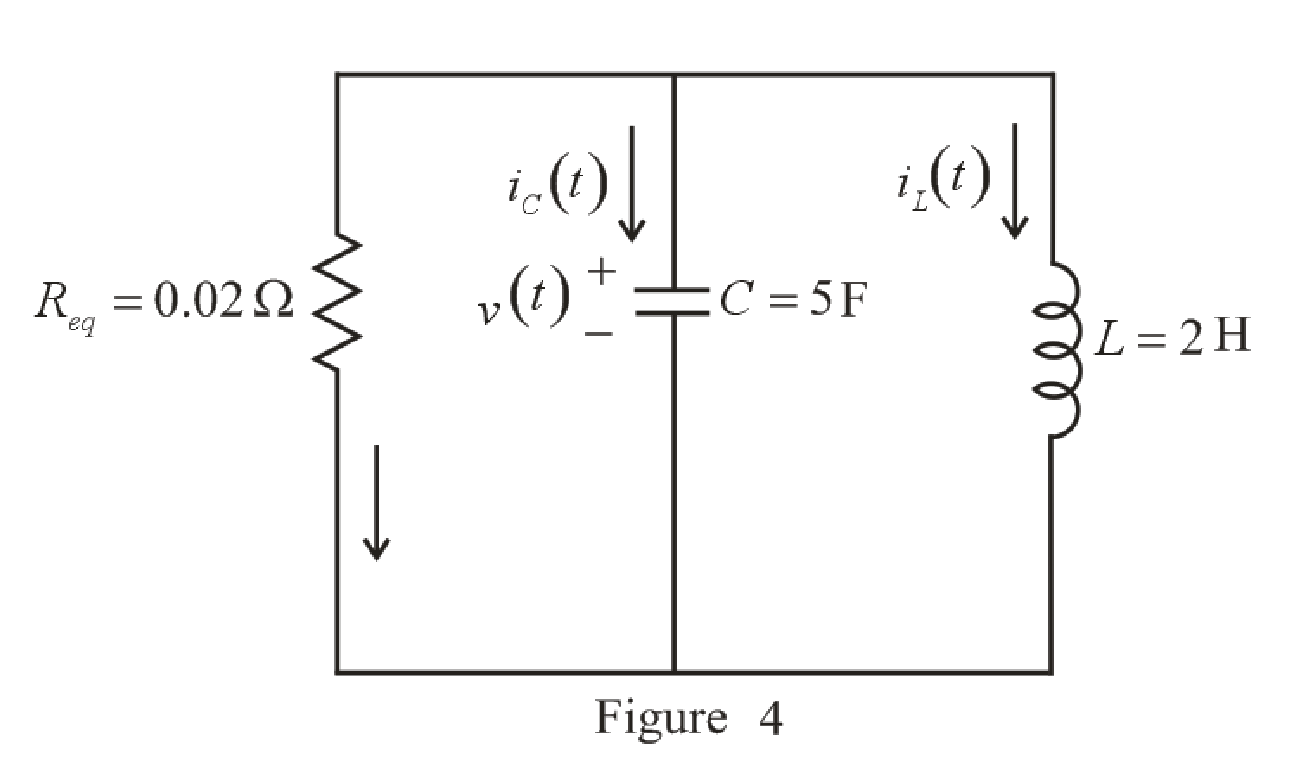
Refer to the redrawn Figure 4:
The expression for the current flowing in the left hand mesh at
Here,
Substitute
Differentiate both side of the equation (19).
The maximum value is obtained when derivative is equated to zero.
Rearrange equation (20).
Take natural logarithm both sides.
Rearrange for
Substitute
So, the value of the maximum current flowing in the left hand mesh is
Settling time is the time at which the value of the current reaches
The expression for the current at
Here,
Substitute
The value of current flowing in the left hand mesh at
Substitute
Since the component
So, the new equation is:
Rearrange equation (22).
Take natural logarithm both sides.
Rearrange for
So, the settling time of the currentflowing in the left hand mesh
Conclusion:
Thus, the settling time of current
Want to see more full solutions like this?
Chapter 9 Solutions
Engineering Circuit Analysis
- 5.25. Determine the corner frequency resulting from Cin in Fig. 5.47(d). For simplicity, assume C₁ is a short circuit. TVDD C₁ M2 RF Vin H w - Vout Cin M₁arrow_forwardIn the below circuit, find out the value of equivalent Thevenin's voltage and Thevenin's resistance at the terminal. 2000 0.25 A 400 2 800 2 0.1 Aarrow_forwardQ1: For the circuit shown in Figure-1, (a) Calculate the equivalent resistance of the circuit, RAB at the terminals A and B. [10] (b) When 50V dc source is switched at terminals A-B, solve for the voltage V₁ at the location shown. [10] 50V www 12Ω 10Ω 5Ω www www A + B 200 Figure-1 www 10Ω ww 25Ω 100arrow_forward
- a. Write a PLC ladder diagram that allows the teacher to teach AND, OR, and XOR logic gates through using three PLC's digital input points and only one digital output point.arrow_forwardrately by PRACTICE 4.2 For the circuit of Fig. 4.5, compute the voltage across each curren source. 202 ww 3A 30 ww 4Ω S 50 www Reference node FIGURE 4.5 Ans: V3A =5.235 V; 7A = 11.47 V. 7 Aarrow_forwardQ2) a) design and show me your steps to convert the following signal from continuous form to digital form: s(t)=3sin(3πt) -1 373 Colesarrow_forward
- A sequence is defined by the relationship r[n] = [h[m]h[n+m]=hn*h-n where h[n] is a minimum-phase sequence and r[n]= 4 4 (u[n]+ 12" [n-1] 3 (a) Find R(z) and sketch the pole-zero diagram. (b) Determine the minimum-phase sequence h[n] to within a scale factor of ±1. Also, determine the z-transform H(z) of h[n].arrow_forwardusıng j-k and D flipflop design a counter that counts 0,2,1 again as shown below ın the tablearrow_forwardfind the minterms of the followıng boolean expressıon desıgn F's cırcuit using one of the approciate decoders given below and a NOR gateF(A,B,C,D)=(A+'BC)(B 'C+'A 'D + CD)arrow_forward
- 64) answer just two from three the following terms: A) Design ADC using the successive method if the Vmax=(3) volt, Vmin=(-2) volt, demonstrate the designing system for vin-1.2 volt. Successive Approximation ADC Input Voltage-1.1 V -4-3.5-3 -2.5 -2 -1.5 +1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 1 T -8 -7 -6 -5 -3 +2 -1 0 1 2 3 4 5 6 7 X=1??? 1st guess: -0.25 V (too high) X=11?? 2nd guess: -2.25 V (too low) 3rd guess: -1.25 V (too low) X=1110 X=111? 4th guess: -0.75 V (too high) Make successive guesses and use a comparator to tell whether your guess is too high or too low. Each guess determines one bit of the answer and cuts the number of remaining possibilities in half.arrow_forwardDatacommunıcatıonin a commuinaction ASYNCHRONOUS TRANSMİTİON is used in this transmistion 7-bit chatacter will be transfered even parity will be used ,stop element is as 1,5 bits a)=select a chracter yourself and dısplay the signal transfered in this transmission , and calculate the overhead in this transmisionarrow_forward(i) Find the inverse z-transform of the system H(z) = for the following regions of convergence. Write in the final answer for each case in the allocated rectangular box below (a) |z| 3 (c) 1arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





