
Concept explainers
(a)
The point moves a greater distance in a given time, if the disk rotates with increasing
(a)
Answer to Problem 1P
The particle on the rim covers a greater linear distance as compared to the particle situated half way between the rim and the axis of rotation.
Explanation of Solution
Given:
A disk rotating with increasing angular velocity about an axis passing through its center and perpendicular to its plane.
Distance of the particle 1 (on the rim) from the axis of rotation
Distance of particle 2 (half way between the axis of rotation and the rim) from the axis of rotation
Here, the radius of the disk is
Formula used:
The
Here,
The angular acceleration of a point on the rotating disk is related to the linear acceleration
Here,
The linear distance
Calculations:
The disk of radius
from the axis of rotation. This is shown in the figure 1 below:
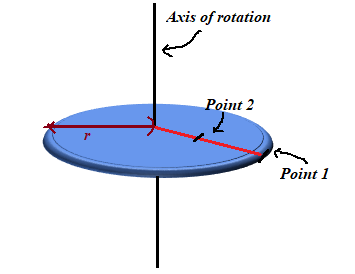
Figure 1
If the disk rotates with an angular acceleration
Calculate the linear accelerations of the particles located at point 1 and 2 using the equation (2).
Substitute
Therefore, from the above equations,
If the disk is assumed to start from rest, both particles would start with their initial velocities
Use equation (3) to calculate the distance travelled by the two points.
From equation (5),
Conclusion:
Therefore, the point on the rim travels a greater distance when compared to the point located halfway between the rim and the axis of rotation.
(b)
The point that turns through a greater angle.
(b)
Answer to Problem 1P
Both the points turn through the same angle.
Explanation of Solution
Formula used:
The
Here
Calculation:
The points 1 and 2 located at points A and B on the disc rotating with an angular acceleration
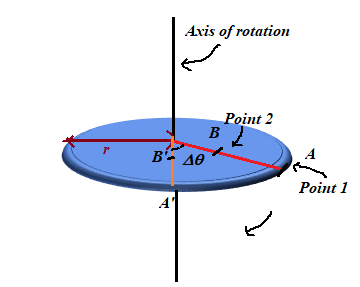
Figure 2
At any instant of time, both particles have the same instantaneous angular velocity and angular acceleration. As it can be seen from Figure 2, both particles describe the same angle at an instant of time.
Conclusion:
Thus, the particle located at the rim and the particle located half way between the rim and the axis of rotation turn through the same angle.
(c)
The point which travels with greater speed.
(c)
Answer to Problem 1P
The point on the rim travels with greater speed.
Explanation of Solution
Formula used:
The instantaneous speed
Here,
Calculation:
The disk moves with increasing angular velocity. But, both points at any instant would have the same instantaneous angular velocity, since they turn through the same angle in a given interval of time.
Hence, it can be inferred from equation (7):
Since the point on the rim has the greater value of
Conclusion:
Thus, the point on the rim would have a greater speed when compared to the point located half way between the rim and the axis of rotation.
(d)
The point which has the greater angular speed.
(d)
Answer to Problem 1P
Both the particles have the same angular speed.
Explanation of Solution
Formula used:
The angular velocity of a particle is given by
Calculation:
From Figure 2, it is seen that at any instant of time, both particles 1 and 2 cover the same angles. Hence, the rate of change of their angular displacement
Conclusion:
Thus, the particle on the rim and the particle located halfway between the rim and the axis of rotation have the same angular velocity.
(e)
The point which has the greater tangential acceleration.
(e)
Answer to Problem 1P
The point on the rim has a greater tangential acceleration when compared to the point located midway between the rim and the axis of rotation:
Explanation of Solution
Formula used:
The tangential acceleration
Calculation:
If the disk rotates with a varying angular velocity, it has angular acceleration. Assuming that the angular acceleration of the disk remains constant, from equation (9) it can be inferred that
The point on the rim has the greater value of
Therefore, the point on the rim has a greater tangential acceleration when compared to any point located inside the rim. This is also proved by the fact that the point on the rim gains a larger tangential velocity when compared to any inner point.
Conclusion:
Thus, the point on the rim has a greater tangential acceleration when compared to the point located midway between the rim and the axis of rotation.
(f)
The point which has a greater angular acceleration.
(f)
Answer to Problem 1P
Both particles have the same angular acceleration.
Explanation of Solution
Formula used:
The angular acceleration
Calculation:
It has been proved in (d) that at any instant of time, both the particles have the same angular velocity. Therefore, in an interval of time
Hence, from equation (1), it can be proved that at a given instant of time, both the points will have the same angular accelerations.
Conclusion:
Thus, both particles are found to have the same angular acceleration.
(g)
The point which has the greater centripetal acceleration.
(g)
Answer to Problem 1P
The point on the rim has a greater centripetal acceleration.
Explanation of Solution
Formula used:
The centripetal acceleration of a point located at a distance
Calculation:
It has been established in part (d) that at any instant of time, the point on the rim and the point located halfway between the rim and the axis of rotation have the same angular velocity.
Therefore, from equation (10), it can be inferred that
The point on the rim has the greater value of
Conclusion:
Thus, the point on the rim has a greater centripetal acceleration.
Want to see more full solutions like this?
Chapter 9 Solutions
Physics for Scientists and Engineers, Vol. 1
- a) Consider the following function, where A is a constant. y(x,t) = A(x — vt). Can this represent a wave that travels along? Explain. b) Which of the following are possible traveling waves, provide your reasoning and give the velocity of the wave if it can be a traveling wave. e-(a²x²+b²²-2abtx b.1) y(x,t) b.2) y(x,t) = = A sin(ax² - bt²). 2 b.3) y(x,t) = A sin 2π (+) b.4) y(x,t) = A cos² 2π(t-x). b.5) y(x,t) = A cos wt sin(kx - wt)arrow_forwardThe capacitor in (Figure 1) is initially uncharged. The switch is closed at t=0. Immediately after the switch is closed, what is the current through the resistor R1, R2, and R3? What is the final charge on the capacitor? Please explain all steps.arrow_forwardSuppose you have a lens system that is to be used primarily for 620-nm light. What is the second thinnest coating of fluorite (calcium fluoride) that would be non-reflective for this wavelength? × nm 434arrow_forward
- The angle between the axes of two polarizing filters is 19.0°. By how much does the second filter reduce the intensity of the light coming through the first? I = 0.106 40 xarrow_forwardAn oil slick on water is 82.3 nm thick and illuminated by white light incident perpendicular to its surface. What color does the oil appear (what is the most constructively reflected wavelength, in nanometers), given its index of refraction is 1.43? (Assume the index of refraction of water is 1.33.) wavelength color 675 × nm red (1 660 nm)arrow_forwardA 1.50 μF capacitor is charging through a 16.0 Ω resistor using a 15.0 V battery. What will be the current when the capacitor has acquired 1/4 of its maximum charge? Please explain all stepsarrow_forward
- In the circuit shown in the figure (Figure 1), the 6.0 Ω resistor is consuming energy at a rate of 24 J/s when the current through it flows as shown. What are the polarity and emf of the battery E, assuming it has negligible internal resistance? Please explain all steps. I know you need to use the loop rule, but I keep getting the answer wrong.arrow_forwardIf you connect a 1.8 F and a 2.6 F capacitor in series, what will be the equivalent capacitance?arrow_forwardSuppose that a particular heart defibrillator uses a 1.5 x 10-5 Farad capacitor. If it is charged up to a voltage of 7300 volts, how much energy is stored in the capacitor? Give your answer as the number of Joules.arrow_forward
- The voltage difference across an 8.3 nanometer thick cell membrane is 6.5 x 10-5volts. What is the magnitude of the electric field inside this cell membrane? (Assume the field is uniform, and give your answer as the number of Volts per meter... which is the same as the number of Newtons per Coulomb.)arrow_forwardThree identical capacitors are connected in parallel. When this parallel assembly of capacitors is connected to a 12 volt battery, a total of 3.1 x 10-5 coulombs flows through the battery. What is the capacitance of one individual capacitor? (Give your answer as the number of Farads.)arrow_forwardSuppose you construct your own capacitor by placing two parallel plates at a distance 0.27 meters apart. The plates each have a surface area of 0.64 square meters. What is the capacitance of this setup? (Give your answer as the number of Farads.)arrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





