Chapter 9, Problem 115QRT

Interpretation Introduction

Interpretation:

The volume of the atoms in bcc and fcc unit cell in comparison to the volume of the unit cell itself has to be calculated.  From these data, the fraction of space occupied by atoms in bcc and fcc unit cell has to be calculated.

Concept Introduction:

Bcc unit cell:

Eight atoms occupy the corner position of a cube each contributing $1/8$ to the unit cell and one atom occupies the body center of the unit cell.  Hence, the total number of atoms present in one unit cell is $8\times \frac{1}{8}+1=2$.

Relationship between unit cell edge length and radius of a unit cell of a bcc arrangement:

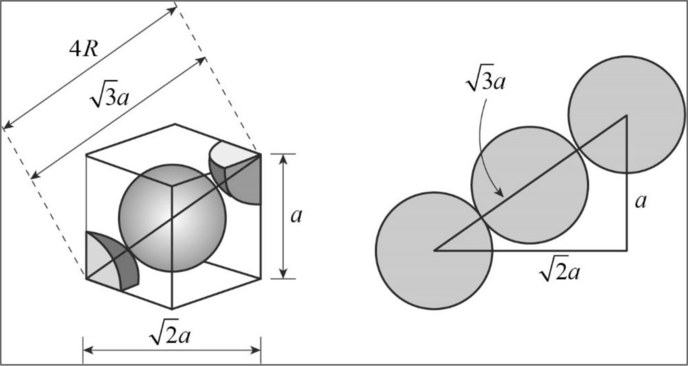
Figure 1

Applying Pythagoras theorem, from the diagram we can clearly concluded that

  Body diagonal $=4R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}}{4}a$

Fcc unit cell:

Eight atoms occupy the corner position of a cube each contributing $1/8$ to the unit cell and six atoms occupy the center of each face of the unit cell contributing $1/2$ to the unit cell.  Hence, the total number of atoms present in one unit cell is $8\times \frac{1}{8}+6\times \frac{1}{2}=4$.

Relationship between unit cell edge length and radius of a unit cell of a fcc arrangement:

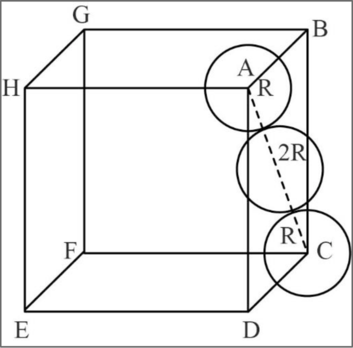
Figure 2

In fcc, the corner spheres are in touch with the face centered sphere as shown in the above figure.  Hence, the face diagonal $AC=4R$.

Consider right angled triangle ACD.

  $\begin{array}{c}{\left(AC\right)}^2={\left(AD\right)}^2+{\left(DC\right)}^2\\ \\ =a^2+a^2=2a^2\\ \\ AC=\sqrt{2}a=4R\\ \\ R=\frac{\sqrt{2}}{4}a\left(or\right)a=\frac{4R}{\sqrt{2}}\end{array}$

Volume of a cubic unit cell:

Volume of cubic unit cell $=a^3$

Volume of a sphere:

Volume of a sphere $=\frac{4}{3}\pi r^3$

Packing fraction:

Packing fraction is the fraction of space occupied by total number of atoms per unit cell.

Mathematically, it can be represented as given below.

Fraction of space occupied by atoms in a unit cell $=\frac{V_{atoms}}{V_{unitcell}}$

Where, $V_{atoms}$$=$ Volume of total number of atoms per unit cell and $V_{unitcell}$ $=$ Volume of a unit cell

Answer to Problem 115QRT

The fraction of space occupied by atoms in bcc and fcc unit cell is $0.680$ and $0.740$ respectively.

Explanation of Solution

The atoms can be assumed to be spherical in shape with radius $r$.  So the volume of one atom can be calculated by using the given below formula.

  $V=\frac{4}{3}\pi r^3$

There are two atoms present per one bcc unit cell.  The relationship between unit cell edge length and radius of a unit cell of a bcc arrangement is given below.

  $r=\frac{\sqrt{3}}{4}a$

Now, the total volume of two atoms present in a bcc unit cell can be calculated as given below.

  $V_{atomsinbcc}=2\times \frac{4}{3}\pi {\left(\frac{\sqrt{3}}{4}a\right)}^3$

There are four atoms present per one fcc unit cell.  The relationship between unit cell edge length and radius of a unit cell of a fcc arrangement is given below.

  $r=\frac{\sqrt{2}}{4}a$

Now, the total volume of two atoms present in a bcc unit cell can be calculated as given below.

  $V_{atomsinfcc}=4\times \frac{4}{3}\pi {\left(\frac{\sqrt{2}}{4}a\right)}^3$

Volume of cubic unit cell , $V_{cubicunitcell}=a^3$

Now, the fraction of space occupied by atoms can be calculated as given below.

For bcc unit cell:

Fraction of space occupied by atoms $=\frac{V_{atomsinbcc}}{V_{bcc}}=\frac{2\times \frac{4}{3}\pi {\left(\frac{\sqrt{3}}{4}a\right)}^3}{a^3}=\mathrm{0.680.}$

For fcc unit cell:

Fraction of space occupied by atoms $=\frac{V_{atomsinfcc}}{V_{fcc}}=\frac{4\times \frac{4}{3}\pi {\left(\frac{\sqrt{2}}{4}a\right)}^3}{a^3}=\mathrm{0.740.}$

Therefore, the fraction of space occupied by atoms in bcc and fcc unit cell is $0.680$ and $0.740$ respectively.