Chapter 9, Problem 101P

Consider a modified form of Couette flow in which there are two immiscible fluids sandwiched between two infinitely lone and wide, parallel flat plates (Fig. 9-101). The flow is steady, incompressible, parallel, and laminar. The top plate moves at velocity V to the right, and the bottom plate is stationary. Gravity acts in the -z-direction (downward in the figure). There is no forced pressure gradient pushing the fluids through the channel-the flow is setup solely by viscous effects created by the moving upper plate. You may ignore surface tension effects and assume that dre interface is horizontal. The pressure at the bottom of the flow (z = 0) is equal to $P_0$ . (a) List all the appropriate boundary conditions on both velocity and pressure. (Hint: There are six required boundary conditions.) (b) Solve for the velocity field. (Hint: Split up the solution into two portions, one for each fluid. Generate expressions for $u_1$as a function of z and $u_2$as a function ofz.) (c) Solve for the pressure field. (Hint: Again split up the solution. Solve for $P_1$and $P_2$ ) (d) Let fluid 1 be water and let fluid 2 be unused engine oil, both at $80°C$ . Also let $h_1=5.0$mm, $h_2=5.0$mm. and V = 10.0 m/s. Plot u as a function of z across the entire channel. Discuss the results.

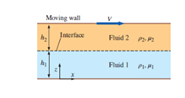
FIGURE P9-101

To determine

(a)

The six appropriate boundary condition on both velocity and pressure.

Answer to Problem 101P

The first boundary conditions is $u_1=0$.

The second boundary conditions is $u_2=h_1+h_2$.

The third boundary conditions is $u_2=u_1$.

The fourth boundary conditions is ${\mu }_1\frac{d{u}_1}{dz}={\mu }_2\frac{d{u}_2}{dz}$.

The fifth boundary conditions is $P=P_0$.

The sixth boundary conditions is $P_1=P_2$.

Explanation of Solution

Given information:

The following figure shows that two parallel flat plates.

  

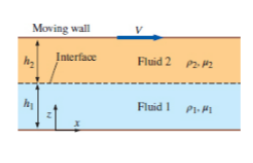
  Figure-( 1)

Assume, at the point of wall and fluid, the velocity of the fluid is equal to zero.

Write the expression for velocity of the fluid 1,

  $u_1=0$   ....... (I)

Here, the velocity of fluid 1 is $u_1$.

Assume, the velocity of the fluid 2 at the free surface of the wall is equal to the velocity of the moving plates.

Write the expressions for the velocity of fluid 2.

  $\begin{array}{c}{u}_2=V\\ =h_1+h_2\end{array}$   ....... (II)

Here, the velocity of fluid 2 is $u_2$, the velocity of the flow is $V$, the height of the fluid 1 from the wall is $h_1$ and the height of the fluid 2 from the interface is $h_2$.

Write the expression for velocity at interface.

  $u_2=u_1$   ....... (III)

Write the expression for rate of shear stress.

  $\tau =\mu \frac{du}{dz}$   ....... (IV)

Here, the kinematic coefficient of fluid is $\mu$ and the rate of shear stress is $\tau$.

Write the expression for the shear stress acting on fluid 1.

  ${\tau }_1={\mu }_1\frac{d{u}_1}{dz}$   ...... (V)

Here, the kinematic coefficient of fluid 1 is ${\mu }_1$ and the shear stress acting on the fluid 1 is ${\tau }_1$.

Write the expression for the shear stress acting on fluid 2.

  ${\tau }_2={\mu }_2\frac{d{u}_2}{dz}$   ....... (VI)

Here, the kinematic coefficient of fluid 2 is ${\mu }_2$ and the shear stress acting on the fluid 2 is ${\tau }_2$.

Write the expression for the rate of shear stress at interface.

  ${\mu }_1\frac{d{u}_1}{dz}={\mu }_2\frac{d{u}_2}{dz}$   ...... (VII)

Write the expression for pressure at the bottom of the flow,

  $P=P_0$   ...... (VIII)

Here, the pressure is $P$ and the pressure at the bottom of the flow is $P_0$.

Write the expression for the pressure at the interface of fluid 1.

  $P=P_1$   ...... (IX)

Here, the pressure at the fluid 1 is $P_1$.

Write the expression for the pressure at the interface of fluid 2.

  $P=P_2$   ....... (X)

Here, the pressure at the fluid 1 is $P_2$.

Assume, at the interface of the fluid the pressure cannot have discontinuity and the surface is ignored.

Write the expression for the pressure at interface of fluid.

  $P_1=P_2$   ...... (XI)

Conclusion:

The first boundary conditions is $u_1=0$.

The second boundary conditions is $u_2=h_1+h_2$.

The third boundary conditions is $u_2=u_1$.

The fourth boundary conditions is ${\mu }_1\frac{d{u}_1}{dz}={\mu }_2\frac{d{u}_2}{dz}$.

The fifth boundary conditions is $P=P_0$.

The sixth boundary conditions is $P_1=P_2$.

To determine

(b)

The expression for the velocity of fluid 1.

The expression for the velocity of fluid 2.

Answer to Problem 101P

The expression for the velocity of fluid 1 is $\left(\frac{{\mu }_2{C}_3}{{\mu }_1}\right)z$.

The expression for the velocity of fluid 2 is $V+\frac{u_1^2}{{\mu }_2{h}_1}\left(z+\left(h_1+h_2\right)\right)$.

Explanation of Solution

Write the expression for $x$ momentum equation of flow for fluid 1.

  $\frac{d^2{u}_1}{d{z}^2}=0$..... (XII)

Here, the velocity of flow for fluid 1 is $u_1$.

Write the expression for $x$ momentum equation of flow for fluid 2.

  $\frac{d^2{u}_2}{d{z}^2}=0$..... (XIII)

Here, the velocity of flow for fluid 2 is $u_2$.

Calculation:

Integrate Equation (XIII) with respect to $z$.

  $\begin{array}{c}{\displaystyle \int \frac{d^2{u}_1}{d{z}^2}}={\displaystyle \int 0}\\ \frac{d{u}_1}{dz}=C_1\end{array}$   ...... (XIV)

Here, the constant is $C_1$.

Integrate Equation (XIII) with respect to $z$.

  $\begin{array}{c}{\displaystyle \int \frac{d{u}_1}{dz}}={\displaystyle \int C_1}\\ u_1=C_1{z}^{0+1}+C_2\\ u_1=C_{1}z+C_2\end{array}$   ....... (XV)

Here, the constant is $C_2$ and the distance is $z$.

Integrate Equation (XIV) with respect to $z$.

  $\begin{array}{c}{\displaystyle \int \frac{d^2{u}_2}{d{z}^2}}={\displaystyle \int 0}\\ \frac{d{u}_2}{dz}=C_3\end{array}$   ...... (XVI)

Here, the constant is $C_3$.

Integrate Equation (XIV) with respect to $z$.

  $\begin{array}{c}{\displaystyle \int \frac{d{u}_2}{dz}}={\displaystyle \int C_3}\\ u_2=C_3{z}^{0+1}+C_4\\ u_2=C_{3}z+C_4\end{array}$   ....... (XVII)

Here, the constant is $C_4$.

Substitute $0$ for $z$ and $0$ for $u_1$ in Equation (XV).

  $\begin{array}{l}0=C_1\left(0\right)+C_2\\ 0=0+C_2\\ C_2=0\end{array}$

Substitute $0$ for $C_2$ and $h_1$ for $z$ in Equation (XV).

  $\begin{array}{l}{u}_1=C_1{h}_1+0\\ u_1=C_1{h}_1\end{array}$   ....... (XVIII)

Substitute $h_1+h_2$ for $z$ and $V$ for $u_2$ in Equation (XVII).

  $V=C_3\left(h_1+h_2\right)+C_4$..... (XIX)

Substitute $h_1$ for $z$ and $u_1$ for $u_2$ in Equation (XVII).

  $u_1=C_3{h}_1+C_4$   ....... (XX)

Substitute $C_{3}z$ for $u_2$ and $C_{1}z$ for $u_1$ in Equation (VII).

  ${\mu }_1\frac{d\left(C_{1}z\right)}{dz}={\mu }_2\frac{d\left(C_{3}z\right)}{dz}$   ...... (XXI)

Differentiate Equation (XXI) with respect to $z$.

  $\begin{array}{l}{\mu }_1{C}_1{z}^{1-1}={\mu }_2{C}_3{z}^{1-1}\\ {\mu }_1{C}_1={\mu }_2{C}_3\\ C_1=\frac{{\mu }_2{C}_3}{{\mu }_1}\end{array}$   ....... (XXII)

Substitute $\frac{{\mu }_2{C}_3}{{\mu }_1}$ for $C_1$ in Equation (XVIII).

  $\begin{array}{l}{u}_1=\frac{{\mu }_2{C}_3}{{\mu }_1}\times h_1\\ \frac{u_1^2}{{\mu }_2{h}_1}=C_3\\ C_3=\frac{u_1^2}{{\mu }_2{h}_1}\end{array}$   ....... (XXIII)

Substitute $\frac{u_1^2}{{\mu }_2{h}_1}$ for $C_3$ in Equation (XIX).

  $\begin{array}{l}V=\frac{u_1^2}{{\mu }_2{h}_1}\left(h_1+h_2\right)+C_4\\ C_4=V-\frac{u_1^2}{{\mu }_2{h}_1}\left(h_1+h_2\right)\end{array}$   ....... (XXIV)

Substitute $V-\frac{u_1^2}{{\mu }_2{h}_1}\left(h_1+h_2\right)$ for $C_4$ and $\frac{u_1^2}{{\mu }_2{h}_1}$ for $C_3$ in Equation (XVII).

  $\begin{array}{l}{u}_2=\frac{u_1^2}{{\mu }_2{h}_1}z+V-\frac{u_1^2}{{\mu }_2{h}_1}\left(h_1+h_2\right)\\ u_2=V+\frac{u_1^2}{{\mu }_2{h}_1}\left(z+\left(h_1+h_2\right)\right)\end{array}$

Substitute $\frac{{\mu }_2{C}_3}{{\mu }_1}$ for $C_1$ and $0$ for $C_2$ in Equation (XV).

  $\begin{array}{l}{u}_1=\left(\frac{{\mu }_2{C}_3}{{\mu }_1}\right)z+0\\ u_1=\left(\frac{{\mu }_2{C}_3}{{\mu }_1}\right)z\end{array}$

Conclusion:

The expression for the velocity of fluid 1 is $\left(\frac{{\mu }_2{C}_3}{{\mu }_1}\right)z$.

The expression for the velocity of fluid 2 is $V+\frac{u_1^2}{{\mu }_2{h}_1}\left(z+\left(h_1+h_2\right)\right)$.

To determine

(c)

The expression for the pressure of fluid 1.

The expression for the pressure of fluid 2.

Answer to Problem 101P

The expression for the pressure of fluid 1 is $-{\rho }_{1}gz+P_o$.

The expression for the pressure of fluid 2 is $P_o+g{\rho }_2{h}_1-gz\left({\rho }_1+{\rho }_2\right)$.

Explanation of Solution

Write the expression for $z$ momentum equation of flow of fluid 1.

  $\frac{d{P}_1}{dz}=-{\rho }_{1}g$   ...... (XXV)

Here, the density of the fluid 1 is ${\rho }_1$ and the acceleration due to gravity is $g$.

Write the expression for $z$ momentum equation of flow of fluid 2.

  $\frac{d{P}_2}{dz}=-{\rho }_{2}g$   ...... (XXVI)

Here, the density of the fluid 2 is ${\rho }_2$.

Calculation:

Integrate Equation (XXV) with respect to $z$.

  $\begin{array}{l}{\displaystyle \int \frac{d{P}_1}{dz}}={\displaystyle \int -{\rho }_{1}g}\\ P_1=-{\rho }_{1}gz+C_5\end{array}$   ...... (XXVII)

Here, the constant is $C_5$.

Substitute $P_o$ for $P_1$ and $0$ for $z$ in Equation (XXVII).

  $\begin{array}{l}{P}_o=-{\rho }_{1}g\left(0\right)+C_5\\ C_5=P_o\end{array}$   ...... (XXVIII)

Substitute $P_o$ for $C_5$ in Equation (XXVII).

  $P_1=-{\rho }_{1}gz+P_o$   ....... (XXIX)

Integrate Equation (XXVI) with respect to $z$.

  $\begin{array}{l}{\displaystyle \int \frac{d{P}_2}{dz}}={\displaystyle \int -{\rho }_{2}g}\\ P_2=-{\rho }_{2}gz+C_6\end{array}$   ....... (XXX)

Here, the constant is $C_6$.

Substitute $P_1$ for $P_2$ and $h_1$ for $z$ in Equation (XXX).

  $P_1=-{\rho }_{2}g{h}_1+C_6$   ....... (XXXI)

Substitute $-{\rho }_{1}gz+P_o$ for $P_1$ in Equation (XXXI).

  $\begin{array}{l}-{\rho }_{1}gz+P_o=-{\rho }_{2}g{h}_1+C_6\\ C_6=-{\rho }_{1}gz+P_o+{\rho }_{2}g{h}_1\\ C_6=P_o+g\left({\rho }_2{h}_1-{\rho }_{1}z\right)\end{array}$   ....... (XXXII)

Substitute $P_o+g\left({\rho }_2{h}_1-{\rho }_{1}z\right)$ for $C_6$ in Equation (XXXI).

  $\begin{array}{c}{P}_2=-{\rho }_{2}gz+P_o+g\left({\rho }_2{h}_1-{\rho }_{1}z\right)\\ =P_o+g{\rho }_2{h}_1-g{\rho }_{1}z-{\rho }_{2}gz\\ =P_o+g{\rho }_2{h}_1-gz\left({\rho }_1+{\rho }_2\right)\end{array}$

Conclusion:

The expression for the pressure of fluid 1 is $-{\rho }_{1}gz+P_o$.

The expression for the pressure of fluid 2 is $P_o+g{\rho }_2{h}_1-gz\left({\rho }_1+{\rho }_2\right)$.

To determine

(d)

The plot $u$ as a function of $z$ across the entire channel.

Answer to Problem 101P

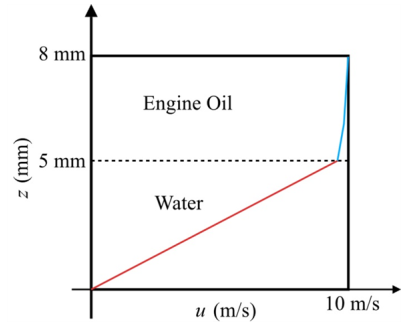
The following Figure-(2) represents the velocities of fluid 1 and 2.

  

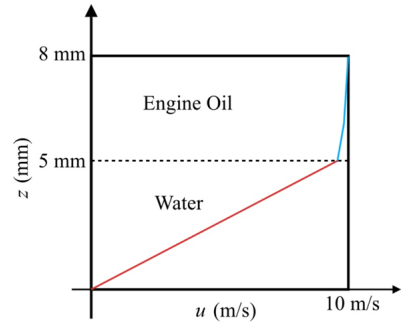
Explanation of Solution

Given information:

The fluid 1 be water and the fluid 2 be unused engine oil, at $80°C$. The height of fluid 1 is $5\text{mm}$ and the height of fluid 2 is $8\text{mm}$. The velocity of flow is $10\text{m}/\text{s}$.

The following figure shows that two parallel flat plates.

Write the expression for the velocity of fluid 1.

  $u_1=\left(\frac{{\mu }_{2}V}{{\mu }_2{h}_1+{\mu }_1{h}_2}\right)z$   ....... (XXXIII)

Here, the distance is $z$, the velocity of fluid 1 is $u_1$, the velocity of fluid 2 is $u_2$, the velocity of the flow is $V$, the height of the fluid 1 from the wall is $h_1$ and the height of the fluid 2 from the interface is $h_2$.

Write the expression for the velocity of fluid 2.

  $u_2=\left(\frac{V}{{\mu }_2{h}_1+{\mu }_1{h}_2}\right)\left[\mu \left(z-h_2\right)+{\mu }_2{h}_1\right]$   ....... (XXXIV)

Calculation:

Refer the Table-A-3E, "Properties of saturated water", to obtain the value of dynamic viscosity of water is $\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}$ corresponding to the temperature $80°C$.

Refer the Table-A-7E, "Properties of the atmosphere at high attitude", to obtain the value of dynamic viscosity of unused engine oil is $\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}$ corresponding to the temperature $80°C$.

Substitute $\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}$ for ${\mu }_2$, $\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}$ for ${\mu }_1$, $10\text{m}/\text{s}$ for $V$, $5\text{mm}$ for $h_1$ and $8\text{mm}$ for $h_2$ in Equation (XXXIII).

  $\begin{array}{c}{u}_1=\left[\frac{\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(10\text{m}/\text{s}\right)}{\left[\begin{array}{l}\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(5\text{mm}\right)\\ +\left(\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}\right)\left(8\text{mm}\right)\end{array}\right]}\right]z\\ =\left(\frac{\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(10\text{m}/\text{s}\right)}{\left[\begin{array}{l}\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(5\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\\ +\left(\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}\right)\left(8\text{mm}\left(\frac{1\text{m}}{1000\text{mm}}\right)\right)\end{array}\right]}\right)z\\ =\left(\frac{\text{2}\text{.958}\text{kg}/{\text{s}}^2}{\left[0.01481\text{kg}/{\text{s}}^2\right]}\right)z\\ =199.72z\end{array}$

Substitute $\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}$ for ${\mu }_2$, $\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}$ for ${\mu }_1$, $10\text{m}/\text{s}$ for $V$, $5\text{mm}$ for $h_1$ and $8\text{mm}$ for $h_2$ in Equation (XXXIV).

  $u_2=\left[\begin{array}{l}\left(\frac{\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(10\text{m}/\text{s}\right)}{\left[\begin{array}{l}\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(5\text{mm}\right)\\ +\left(\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}\right)\left(8\text{mm}\right)\end{array}\right]}\right)\\ \left[\begin{array}{l}\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}\times \left(z-8\text{mm}\right)+\\ \left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\times 5\text{mm}\end{array}\right]\end{array}\right]$

  $=\left[\begin{array}{l}\left(\frac{\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(10\text{m}/\text{s}\right)}{\left[\begin{array}{l}\left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\left(5\text{mm}\left(\frac{1\text{m}}{1000\text{cm}}\right)\right)\\ +\left(\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}\right)\left(8\text{mm}\left(\frac{1\text{m}}{1000\text{cm}}\right)\right)\end{array}\right]}\right)\\ \left[\begin{array}{l}\text{0}\text{.355}\times {\text{10}}^{-3}\text{kg}/\text{m}\cdot \text{s}\times \left(z-0.08\text{m}\right)+\\ \left(\text{0}\text{.2958}\text{kg}/\text{m}\cdot \text{s}\right)\times 0.05\text{m}\end{array}\right]\end{array}\right]$

  $=199.72\text{kg}/{\text{s}}^2\times \left(0.355z-1.47\right)\text{kg}/{\text{s}}^2$

The following graph represents the velocities of fluid 1 and 2.

  

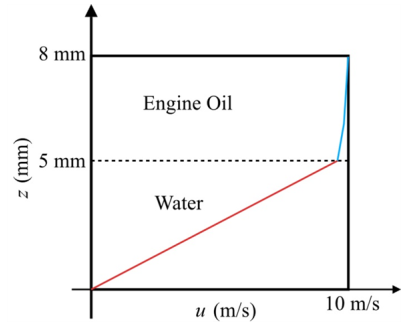
  Figure-(2)

In the fluid 1 the linear curve is increasing with respect to the velocity of flow and height of fluid 1. In the fluid 2 the curve is increasing with respect to the velocity of flow and height of fluid 2.

Conclusion:

The following Figure-(2) represents the velocities of fluid 1 and 2.