
Concept explainers
Interpretation:
For anoverdamped system forced by a square wave given by
Concept Introduction:
Poincare map is defined by
Answer to Problem 3E
Solution:
a)
b)
c) The limits of
d) The Poincare map
e) Using a cobweb picture,
Explanation of Solution
a)
The given system equations are
Multiply the complete equation by
Integrate it with respect to
But,
Divide the complete equation by
Rearrange it as:
Let
Hence, it is proved.
b)
Suppose that the system has a T-periodic solution. Then,
But
Rearrange it as
Hence, it is proved.
c)
Similarly,
These results are plausible. Since as
As
And the solution becomes
d)
Since,
In a general form, it can be written as
It is a straight line equation of the form
The plot of
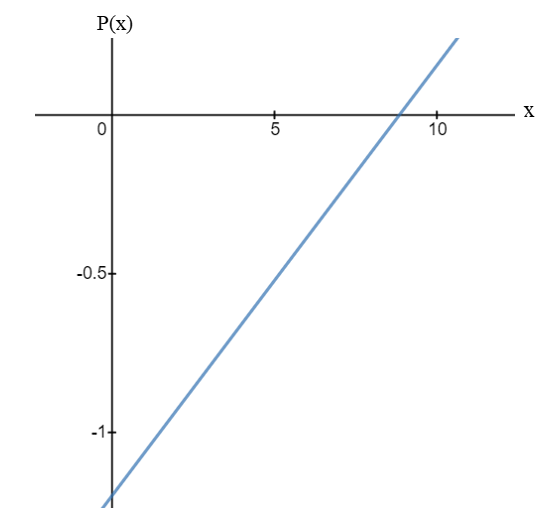
e)
The cobweb plot of the given system at
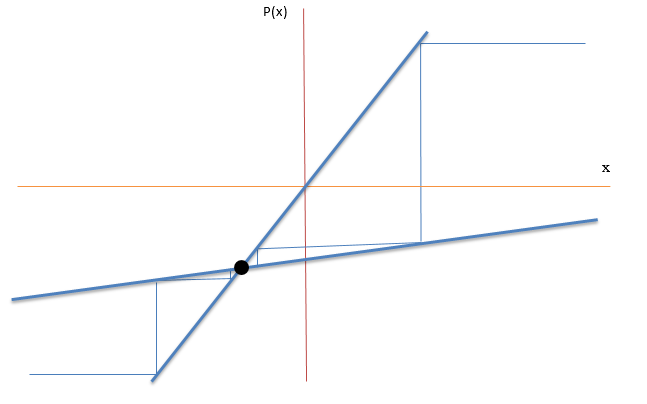
Since
Want to see more full solutions like this?
Chapter 8 Solutions
Nonlinear Dynamics and Chaos
- Pls help asaparrow_forwarda. f(x) = 3 — — x 13. Which of the following has a horizontal asymptote at y = 0 ? 1 - X c. f(x) = 1 b. f(x) == X+2 1 = d. all of the above 17x+4 1 14. What is true about the function f(x)= as x∞o? x+4 a. f(x)0 from above b. f(x)0 from below c. f(x) → 1/1/1 d. f(x)→ ∞ 15. Which function is always positive? a. f(x)= 2 5x+4 1 1 b. f(x)= c. f(x)= d. B and C x²-2x-15 (x-5)²arrow_forwardPls help asaparrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
