Chapter 8.2, Problem 17E

Interpretation Introduction

Interpretation:

To show ${\text{x}}_{\text{1}}^{\text{*}}{\text{= y}}_{\text{2}}^{\text{*}}{\text{= x}}_{\text{2}}^{\text{*}}{\text{= y}}_{\text{2}}^{\text{*}}\text{= u}$ is afixed point for any value of parameter, where u is uniquely defined.

To show the Jacobian matrix for the linearization has the form

$\left(\begin{array}{cccc}{\text{-c}}_{\text{1}}& {\text{-c}}_{\text{2}}& {\text{-c}}_{\text{3}}& \text{0}\\ {\text{d}}_{\text{1}}& {\text{-d}}_{\text{1}}& \text{0}& \text{0}\\ {\text{-c}}_{\text{3}}& \text{0}& {\text{-c}}_{\text{1}}& {\text{-c}}_{\text{2}}\\ \text{0}& \text{0}& {\text{d}}_{\text{1}}& {\text{-d}}_{\text{1}}\end{array}\right)$ and express this matrix in the block-matrix $\left(\begin{array}{cc}\text{A}& \text{B}\\ \text{B}& \text{A}\end{array}\right)$.

Here, A and B are $2\times 2$ matrices. The eigenvalues of the $4\times 4$ block matrix are given by eigenvalues of $\text{A - B and A + B}$

By considering trace and determinant of matrix $\text{A + B}$, show that the all eigenvalues of the matrix are negative.

To show that depending on the sizes of g and T, the determinant of matrix $\text{A - B}$ can be negative (pitchfork bifurcation of u) or positive trace (Hopf bifurcation).

By using computer, show that Hopf bifurcation can be supercritical.

Concept Introduction:

To find fixed point of the system, put $\dot{\text{x}}\text{ = 0 and }\dot{\text{y}}\text{ = 0}$

Jacobian matrix is used to check the stability of the fixed points, and it is given as:

$\text{J}=\left(\begin{array}{cccc}\frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{y}}_{\text{2}}}\\ \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{y}}_{\text{2}}}\\ \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{y}}_{\text{2}}}\\ \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{y}}_{\text{2}}}\end{array}\right)$

The system which is settling down to equilibrium by exponentially damping and its decay rate depends on a control parameter $\mu$. If system is initially stabilizing slowly and gets unstable after $\mu >{\mu }_c$, then it is said that the system has gone through supercritical Hopf bifurcation.

Answer to Problem 17E

Solution:

${\text{x}}_{\text{1}}^{\text{*}}{\text{= y}}_{\text{2}}^{\text{*}}{\text{= x}}_{\text{2}}^{\text{*}}{\text{= y}}_{\text{2}}^{\text{*}}\text{= u}$ is a fixed point for any value of parameter is shown below.

It is shown that the Jacobian matrix for the linearization has the form

$\left(\begin{array}{cccc}{\text{-c}}_{\text{1}}& {\text{-c}}_{\text{2}}& {\text{-c}}_{\text{3}}& \text{0}\\ {\text{d}}_{\text{1}}& {\text{-d}}_{\text{1}}& \text{0}& \text{0}\\ {\text{-c}}_{\text{3}}& \text{0}& {\text{-c}}_{\text{1}}& {\text{-c}}_{\text{2}}\\ \text{0}& \text{0}& {\text{d}}_{\text{1}}& {\text{-d}}_{\text{1}}\end{array}\right)$.

It is shown that all eigenvalues of the matrix $\text{A + B}$ are negative.

It is shown that values of g and T determine whether the determinant of matrix $\text{A - B}$ can be negative (pitchfork bifurcation of u) or positive trace (Hopf bifurcation).

It is shown that the system goes through supercritical Hopf bifurcation.

Explanation of Solution

a)

The system equations are:

$\begin{array}{l}{\dot{\text{x}}}_{\text{1}}{\text{ = - x}}_{\text{1}}\text{ + F}\left({\text{I - bx}}_{\text{2}}{\text{ - gy}}_{\text{1}}\right)\\ {\dot{\text{y}}}_{\text{1}}\text{ = }\left({\text{- y}}_{\text{1}}{\text{ + x}}_{\text{1}}\right)\text{ / T}\\ {\dot{\text{x}}}_{\text{2}}{\text{ = - x}}_{\text{2}}\text{ + F}\left({\text{I - bx}}_{\text{1}}{\text{ - gy}}_{\text{2}}\right)\\ {\dot{\text{y}}}_{\text{2}}\text{ = }\left({\text{- y}}_{\text{2}}{\text{ + x}}_{\text{2}}\right)\text{ / T}\end{array}$

$\text{F(x) = }\frac{1}{{\text{ (1 + e}}^{\text{-x}}\text{)}}$

Assuming that ${\text{x}}_{\text{1}}^{\text{*}}{\text{= y}}_{\text{2}}^{\text{*}}{\text{= x}}_{\text{2}}^{\text{*}}{\text{= y}}_{\text{2}}^{\text{*}}\text{= u}$ is a fixed point for any value of parameter, the system equations are:

$\begin{array}{l}{\dot{\text{x}}}_{\text{1}}\text{ = - u + F}\left(\text{I - bu - gu}\right)\\ {\dot{\text{y}}}_{\text{1}}\text{ = }\left(\text{- u + u}\right)\text{ / T = 0}\\ {\dot{\text{x}}}_{\text{2}}\text{ = - u + F}\left(\text{I - bu - gu}\right)\\ {\dot{\text{y}}}_{\text{2}}\text{ = }\left(\text{- u + u}\right)\text{ / T = 0}\end{array}$

Here, the condition of ${\dot{\text{y}}}_{\text{1}}={\dot{\text{y}}}_2=0$ is satisfied. The condition for ${\dot{\text{x}}}_1{\text{= }\dot{\text{x}}}_1\text{ = 0}$ is:

$\text{0 = - u + F}\left(\text{I - bu - gu}\right)$

$\text{u = F}\left(\text{I - bu - gu}\right)$

$\text{ u =}\frac{\text{1}}{{\text{1+e}}^{\text{- }\left(\text{ I - bu - gu}\right)}}$

In above equation, L.H.S. and R.H.S. are zero and positive respectively when $\text{u = 0}$ and also strictly increasing and decreasing respectively if L.H.S. is greater than R.H.S. and maximum at $\text{u = 0}$ for positive finite value of $\text{u}$.

Thus, the curves intersect and have unique symmetric solution.

b)

The Jacobian matrix is:

$\text{J}=\left(\begin{array}{cccc}\frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{x}}}_{\text{1}}}{\partial {\text{y}}_{\text{2}}}\\ \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{y}}}_{\text{1}}}{\partial {\text{y}}_{\text{2}}}\\ \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{x}}}_{\text{2}}}{\partial {\text{y}}_{\text{2}}}\\ \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{x}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{y}}_{\text{1}}}& \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{x}}_{\text{2}}}& \frac{\partial {\dot{\text{y}}}_{\text{2}}}{\partial {\text{y}}_{\text{2}}}\end{array}\right)$

$\text{J}=\left(\begin{array}{cccc}-1& \frac{-{\text{ge}}^{-{\text{I+bx}}_{\text{2}}{\text{+gy}}_1}}{{\left(1+e^{-{\text{I+bx}}_{\text{2}}{\text{+gy}}_{\text{1}}}\right)}^2}& \frac{-{\text{be}}^{-{\text{I+gx}}_{\text{2}}{\text{+gy}}_1}}{{\left(1+e^{-{\text{I+bx}}_{\text{2}}{\text{+gy}}_{\text{1}}}\right)}^2}& 0\\ \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}& 0& 0\\ \frac{-{\text{be}}^{-{\text{I+bx}}_1{\text{+gy}}_2}}{{\left(1+e^{-{\text{I+bx}}_1{\text{+gy}}_2}\right)}^2}& 0& -1& \frac{-{\text{ge}}^{-{\text{I+bx}}_1{\text{+gy}}_2}}{{\left(1+e^{-{\text{I+bx}}_1{\text{+gy}}_2}\right)}^2}\\ 0& 0& \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}\end{array}\right)$

$\begin{array}{l}\frac{{\text{e}}^{-\text{I+bu+gu}}}{{\left(1+e^{-\text{I+bu+gu}}\right)}^2}=\frac{{\text{1+e}}^{-\text{I+bu+gu}}}{{\left(1+e^{-\text{I+bu+gu}}\right)}^2}-\frac{1}{{\left(1+e^{-\text{I+bu+gu}}\right)}^2}\\ \text{ =}\frac{\text{1}}{\left(1+e^{-\text{I+bu+gu}}\right)}-\frac{1}{{\left(1+e^{-\text{I+bu+gu}}\right)}^2}\\ {\text{ = F(I - bu - gu) - F}}^2\text{(I - bu - gu)}\\ {\text{ = u - u}}^2\end{array}$

${\text{J}}_{\left(\text{u,u,u,u}\right)}=\left(\begin{array}{cccc}-1& -\text{g}\left({\text{u - u}}^2\right)& -\text{b}\left({\text{u - u}}^2\right)& 0\\ \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}& 0& 0\\ -\text{b}\left({\text{u - u}}^2\right)& 0& -1& -\text{g}\left({\text{u - u}}^2\right)\\ 0& 0& \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}\end{array}\right)$

To prove determinant law,

$\left|\begin{array}{cccc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}& \text{b}& \text{0}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}& \text{0}& \text{0}\\ \text{b}& \text{0}& {\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}\\ \text{0}& \text{0}& {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,1}}\end{array}\right|$

Expanding along last column,

$-{\text{a}}_{\text{1,2}}\left|\begin{array}{ccc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}& \text{b}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}& \text{0}\\ \text{0}& \text{0}& {\text{a}}_{\text{1,1}}\end{array}\right|+{\text{a}}_{\text{2,2}}\left|\begin{array}{ccc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}& \text{b}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}& \text{0}\\ \text{0}& \text{0}& {\text{a}}_{\text{1,1}}\end{array}\right|$

Again expanding along bottom row,

$-{\text{a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}\end{array}\right|{\text{+a}}_{\text{1,2}}\text{b}\left|\begin{array}{cc}{\text{a}}_{\text{1,2}}& \text{b}\\ {\text{a}}_{\text{2,2}}& \text{0}\end{array}\right|{\text{+a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}\end{array}\right|$

${\text{- a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}\end{array}\right|\text{-}{\left({\text{a}}_{\text{2,2}}\text{b}\right)}^2{\text{+a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}\end{array}\right|$

$\left({\text{a}}_{\text{1,1}}{\text{a}}_{\text{2,2}}-{\text{a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\right)\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}& {\text{a}}_{\text{1,2}}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}\end{array}\right|\text{-}{\left({\text{a}}_{\text{2,2}}\text{b}\right)}^2$

${\left({\text{a}}_{\text{1,1}}{\text{a}}_{\text{2,2}}-{\text{a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\right)}^2\text{-}{\left({\text{a}}_{\text{2,2}}\text{b}\right)}^2$

$\left(\left({\text{a}}_{\text{1,1}}{\text{a}}_{\text{2,2}}-{\text{a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\right)+{\text{a}}_{\text{2,2}}\text{b}\right)\left(\left({\text{a}}_{\text{1,1}}{\text{a}}_{\text{2,2}}-{\text{a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\right){\text{- a}}_{\text{2,2}}\text{b}\right)$

$\left(\left({\text{a}}_{\text{1,1}}+\text{b}\right){\text{a}}_{\text{2,2}}{\text{- a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\right)\left(\left({\text{a}}_{\text{1,1}}\text{- b}\right){\text{a}}_{\text{2,2}}{\text{- a}}_{\text{1,2}}{\text{a}}_{\text{2,1}}\right)$

$\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}+\text{b}& a_{1,2}\\ a_{2,1}& a_{2,2}\end{array}\right|\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}\text{- b}& a_{1,2}\\ a_{2,1}& a_{2,2}\end{array}\right|$

Therefore,

$\left|\begin{array}{cc}\text{A}& \text{B}\\ \text{B}& \text{A}\end{array}\right|\text{=}\left|\text{A + B}\right|\left|\text{B - A}\right|$

This result is used for calculation of eigenvalues of the $4\times 4$ matrix.

$\left|\begin{array}{cccc}-1-\lambda & -\text{g}\left({\text{u - u}}^2\right)& -\text{b}\left({\text{u - u}}^2\right)& 0\\ \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}-\lambda & 0& 0\\ -\text{b}\left({\text{u - u}}^2\right)& 0& -1-\lambda & -\text{g}\left({\text{u - u}}^2\right)\\ 0& 0& \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}-\lambda \end{array}\right|=0$

$\left|\begin{array}{cc}-1-\text{b}\left({\text{u - u}}^2\right)-\lambda & -\text{g}\left({\text{u - u}}^2\right)\\ \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}-\lambda \end{array}\right|\left|\begin{array}{cc}-1+\text{b}\left({\text{u - u}}^2\right)-\lambda & -\text{g}\left({\text{u - u}}^2\right)\\ \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}-\lambda \end{array}\right|=0$

c)

Using determinant is product of the eigenvalues and trace is sum of eigenvalues,

$\left|\begin{array}{cc}-1-\text{b}\left({\text{u - u}}^2\right)-\lambda & -\text{g}\left({\text{u - u}}^2\right)\\ \frac{\text{1}}{\text{T}}& -\frac{\text{1}}{\text{T}}-\lambda \end{array}\right|$

$\begin{array}{l}\Delta =\left(-1-\text{b}\left({\text{u - u}}^2\right)\right)\left(-\frac{\text{1}}{\text{T}}\right)-\left(-\text{g}\left({\text{u - u}}^2\right)\right)\left(\frac{\text{1}}{\text{T}}\right)\\ \text{ =}\frac{\text{1+}\left(\text{b+g}\right)\left({\text{u - u}}^{\text{2}}\right)}{\text{T}}={\lambda }_1{\lambda }_2\end{array}$

But $\text{u = F}\left(\text{I - bu - gu}\right)=\frac{\text{1}}{{\text{1+e}}^{\text{- }\left(\text{ I - bu - gu}\right)}}$

Here, $0<u<1$ because ${\text{0< F|}}_{u=0}<1$ and F are strictly decreasing. Thus, the intersection will occurfor $0<u<1$.

$\therefore {\text{u - u}}^{\text{2}}>0$ and $0<\frac{\text{1+}\left(\text{b+g}\right)\left({\text{u - u}}^{\text{2}}\right)}{\text{T}}={\lambda }_1{\lambda }_2$

From the above result, ${\text{λ}}_{\text{1}}{\text{,λ}}_{\text{2}}$ both are positive or negative.

The trace $\text{τ}$ is:

$\tau =-1-\text{b(u}-{\text{u}}^{\text{2}})-\frac{\text{1}}{\text{T}}={\text{λ}}_{\text{1}}{\text{+λ}}_{\text{2}}$

$0>-1-\text{b(u}-{\text{u}}^{\text{2}})-\frac{\text{1}}{\text{T}}={\text{λ}}_{\text{1}}{\text{+λ}}_{\text{2}}$

Thus, ${\text{λ}}_{\text{1}}{\text{,λ}}_{\text{2}}$ both are negative.

d)

For the matrix $\text{A-B = }\left|\begin{array}{cc}{\text{a}}_{\text{1,1}}\text{- b}& {\text{a}}_{\text{1,2}}\\ {\text{a}}_{\text{2,1}}& {\text{a}}_{\text{2,2}}\end{array}\right|\text{ = }\left|\begin{array}{cc}{\text{-1 + b(u - u}}^{\text{2}}\text{)}& {\text{-g(u - u}}^{\text{2}}\text{)}\\ \frac{\text{1}}{\text{T}}& \text{-}\frac{\text{1}}{\text{T}}\end{array}\right|$,

The determinant $\Delta =\left(-1+\text{b}(\text{u}-{\text{u}}^2)\right)\left(-\frac{\text{1}}{\text{T}}\right)-\left(-\text{g}(\text{u}-{\text{u}}^2)\right)\left(\frac{\text{1}}{\text{T}}\right)$

$\therefore \Delta =\frac{1+\left(\text{g}-\text{b}\right)\left(\text{u}-{\text{u}}^{\text{2}}\right)}{\text{T}}$,

And trace $\text{τ}=-1+\text{b(u}-{\text{u}}^{\text{2}})-\frac{\text{1}}{\text{T}}$.

From the above results, the determinant is positive if $\text{g > b}$ and negative if $\text{b > g}$.

Trace can negative or positive depending upon values of b and T.

From the above conclusions of eigenvalues, pitchfork or Hopf bifurcation can occur at the point $\left(\text{u,u,u,u}\right)$ by varying parameters g and T.

By adjusting parameter g, if initially trace is negative, and by varying parameter g, its value is shifting towards positive value, then the pitchfork bifurcation occurs at $\left(\text{u,u,u,u}\right)$ when the sign of determinant is switched.

By adjusting parameter T, if the determinant is positive, by changing the parameter T, the trace of the matrix changes its sign, then the Hopf bifurcation occurs at a $\left(\text{u,u,u,u}\right)$.

e)

The plots of $\text{z(t)}$ for three values of T are shown below.

For T being very small, the system is nearly settled down to fixed point $\left(\text{u,u,u,u}\right)$.

Increasing the value of T, the stable limit cycles just appear.

Further increasing the value of T, the size of the limit cycle increases.

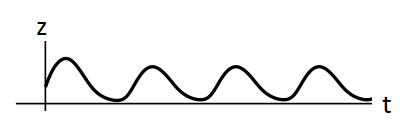
Therefore, the system goes through supercritical Hopf bifurcation.