
a.
Construct a linear regression model for the data.
Test whether there is enough evidence to conclude that
Test whether there is enough evidence to conclude that
a.
Answer to Problem 8E
A simple linear regression model for the data is:
No, there is not enough evidence to conclude that
No, there is not enough evidence to conclude that
Explanation of Solution
Given info:
The data represents the values of the variables amount of deflection in mm
Calculation:
Linear regression model:
A linear regression model is given as
A linear regression model is given as
Regression:
Software procedure:
Step by step procedure to obtain regression using MINITAB software is given as,
- Choose Stat > Regression > General Regression.
- In Response, enter the numeric column containing the response data Y.
- In Model, enter the numeric column containing the predictor variables X.
- Click OK.
Output obtained from MINITAB is given below:

The ‘Coefficient’ column of the regression analysis MINITAB output gives the slopes corresponding to the respective variables stored in the column ‘Term’.
A careful inspection of the output shows that the fitted model is:
Hence, the linear regression model for the data is:
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, intercept of the regression model is not significant.
Alternative hypothesis:
That is, intercept of the regression model is significant.
Level of significance:
Since, the level of significance is not given. The prior level of significance
The ‘P’ column of the regression analysis MINITAB output gives the P- value corresponding to the respective variables stored in the column ‘Term’.
The P- value corresponding to the coefficient
Decision criteria based on P-value approach:
If
If
Conclusion:
The P-value is 0.000 and
Here, P-value is less than the
That is
By the rejection rule, reject the null hypothesis.
Therefore, intercept of the regression model is significant.
Thus, there is not enough evidence to conclude that
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, slope coefficient of the predictor variable distance is not significant.
Alternative hypothesis:
That is, slope coefficient of the predictor variable distance is significant.
From the MINITAB output, the P- value corresponding to the coefficient
Conclusion:
The P-value is 0.001 and
Here, P-value is less than the
That is
By the rejection rule, reject the null hypothesis.
Therefore, the slope coefficient of the predictor variable distance is significant.
Thus, there is not enough evidence to conclude that
b.
Construct a quadratic regression model for the data.
Test whether there is enough evidence to conclude that
Test whether there is enough evidence to conclude that
Test whether there is enough evidence to conclude that
b.
Answer to Problem 8E
The quadratic regression model for the data is
No, there is not enough evidence to conclude that
No, there is not enough evidence to conclude that
Yes, there is enough evidence to conclude that
Explanation of Solution
Calculation:
Quadratic model:
The quadratic regression model would be of the form:
Regression:
Software procedure:
Step by step procedure to obtain quadratic regression model using MINITAB software is given as,
- Choose Stat > Regression > General Regression.
- In Response, enter the numeric column containing the response data Y.
- In Model, enter the numeric column containing the predictor variables X and X-square.
- Click OK.
Output obtained from MINITAB is given below:
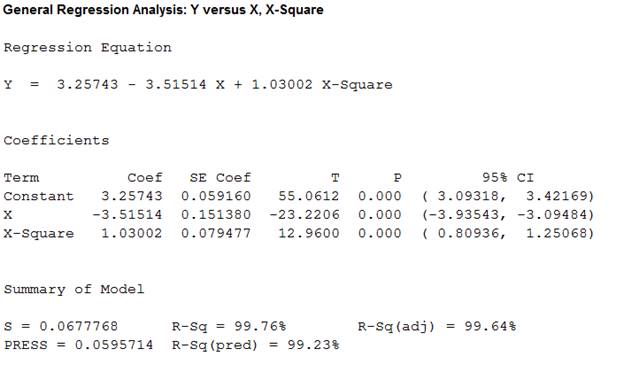
The ‘Coefficient’ column of the
A careful inspection of the output shows that the fitted model is:
Hence, the quadratic regression model for the data is:
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, intercept of the regression model is not significant.
Alternative hypothesis:
That is, intercept of the regression model is significant.
Level of significance:
Since, the level of significance is not given. The prior level of significance
The ‘P’ column of the regression analysis MINITAB output gives the P- value corresponding to the respective variables stored in the column ‘Term’.
The P- value corresponding to the coefficient
Decision criteria based on P-value approach:
If
If
Conclusion:
The P-value is 0.000 and
Here, P-value is less than the
That is
By the rejection rule, fail to reject the null hypothesis.
Therefore, intercept of the regression model is significant.
Thus, there is not enough evidence to conclude that
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, coefficient of the predictor variable distance is not significant.
Alternative hypothesis:
That is, coefficient of the predictor variable distance is significant.
From the MINITAB output, the P- value corresponding to the coefficient
Conclusion:
The P-value is 0.000 and
Here, P-value is less than the
That is
By the rejection rule, fail to reject the null hypothesis.
Therefore, coefficient of the predictor variable distance is significant.
Thus, there is not enough evidence to conclude that
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, coefficient of the predictor variable distance square is not significant.
Alternative hypothesis:
That is, coefficient of the predictor variable distance square is significant.
From the MINITAB output, the P- value corresponding to the coefficient
Conclusion:
The P-value is 0.000 and
Here, P-value is less than the
That is
By the rejection rule, fail to reject the null hypothesis.
Therefore, the coefficient of the predictor variable distance square is significant.
Thus, there is not enough evidence to conclude that
c.
Construct a cubic regression model for the data.
Test whether there is enough evidence to conclude that
Test whether there is enough evidence to conclude that
Test whether there is enough evidence to conclude that
Test whether there is enough evidence to conclude that
c.
Answer to Problem 8E
The quadratic regression model for the data is
No, there is enough evidence to conclude that
No, there is enough evidence to conclude that
Yes, there is enough evidence to conclude that
Yes, there is enough evidence to conclude that
Explanation of Solution
Calculation:
Cubic model:
The cubic regression model would be of the form:
Regression:
Software procedure:
Step by step procedure to obtain cubic regression model using MINITAB software is given as,
- Choose Stat > Regression > General Regression.
- In Response, enter the numeric column containing the response data Y.
- In Model, enter the numeric column containing the predictor variables X, X-square and X-cube.
- Click OK.
Output obtained from MINITAB is given below:
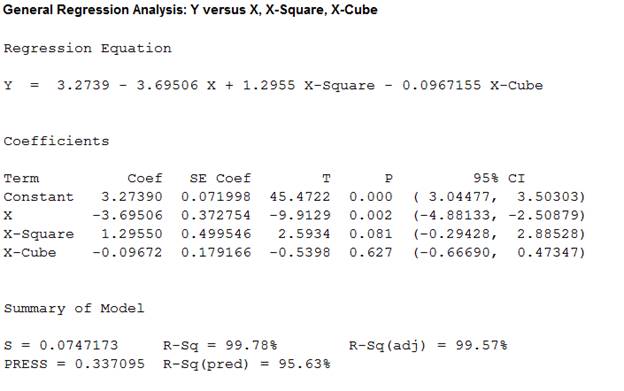
The ‘Coefficient’ column of the regression analysis MINITAB output gives the slopes corresponding to the respective variables stored in the column ‘Predictor’.
A careful inspection of the output shows that the fitted model is:
Hence, the cubic regression model for the data is:
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, intercept of the regression model is not significant.
Alternative hypothesis:
That is, intercept of the regression model is significant.
Level of significance:
Since, the level of significance is not given. The prior level of significance
The ‘P’ column of the regression analysis MINITAB output gives the P- value corresponding to the respective variables stored in the column ‘Term’.
The P- value corresponding to the coefficient
Decision criteria based on P-value approach:
If
If
Conclusion:
The P-value is 0.000 and
Here, P-value is less than the
That is
By the rejection rule, reject the null hypothesis.
Therefore, intercept of the regression model is significant.
Thus, there is not enough evidence to conclude that
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, coefficient of the predictor variable distance is not significant.
Alternative hypothesis:
That is, coefficient of the predictor variable distance is significant.
From the MINITAB output, the P- value corresponding to the coefficient
Conclusion:
The P-value is 0.002 and
Here, P-value is less than the
That is
By the rejection rule, reject the null hypothesis.
Therefore, coefficient of the predictor variable distance is significant.
Thus, there is not enough evidence to conclude that
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, coefficient of the predictor variable distance square is not significant.
Alternative hypothesis:
That is, coefficient of the predictor variable distance square is significant.
From the MINITAB output, the P- value corresponding to the coefficient
Conclusion:
The P-value is 0.081 and
Here, P-value is greater than the
That is
By the rejection rule, fail to reject the null hypothesis.
Therefore, the coefficient of the predictor variable distance square is not significant.
Thus, there is enough evidence to conclude that
Test for slope coefficient
The test hypotheses are given below:
Null hypothesis:
That is, coefficient of the predictor variable distance cube is not significant.
Alternative hypothesis:
That is, coefficient of the predictor variable distance cube is significant.
From the MINITAB output, the P- value corresponding to the coefficient
Conclusion:
The P-value is 0.627 and
Here, P-value is greater than the
That is
By the rejection rule, fail to reject the null hypothesis.
Therefore, the coefficient of the predictor variable distance cube is not significant.
Thus, there is enough evidence to conclude that
d.
Find the best model among the three models obtained in part (a), part (b) and part (c).
d.
Answer to Problem 8E
The model obtained in part (b) is the best model compared to the other two models in part (a) and part (c).
Explanation of Solution
Calculation:
In the model obtained in part (b), all the coefficients of the model are significantly different from zero.
The coefficient of determination is higher for the model obtained in part (b), than for the model obtained in part (a).
That is,
There is not much difference in the coefficient of determination for the model obtained in part (b) and part (c).
That is, 0.9976% and 0.9978% are not much distinct.
Increasing the number of predictors in an analysis increases the complexity of analysis. An investigator usually does not wish to increase the complications of analysis for such a small increase in
Thus, the model obtained in part (b) is the best model compared to the other two models in part (a) and part (c).
e.
Estimate the amount of deflection at a distance of 1m using the most appropriate method.
e.
Answer to Problem 8E
The estimate of the amount of deflection at a distance of 1m is 0.77231mm.
Explanation of Solution
Calculation:
The quadratic model is the most appropriate regression model among the obtained three models.
The quadratic regression model is,
Here,
Estimate of amount of deflection:
Thus, the estimate of the amount of deflection at a distance of 1m is 0.77231mm.
Want to see more full solutions like this?
Chapter 8 Solutions
EBK STATISTICS FOR ENGINEERS AND SCIENT
- Calculate the 90% confidence interval for the population mean difference using the data in the attached image. I need to see where I went wrong.arrow_forwardMicrosoft Excel snapshot for random sampling: Also note the formula used for the last column 02 x✓ fx =INDEX(5852:58551, RANK(C2, $C$2:$C$51)) A B 1 No. States 2 1 ALABAMA Rand No. 0.925957526 3 2 ALASKA 0.372999976 4 3 ARIZONA 0.941323044 5 4 ARKANSAS 0.071266381 Random Sample CALIFORNIA NORTH CAROLINA ARKANSAS WASHINGTON G7 Microsoft Excel snapshot for systematic sampling: xfx INDEX(SD52:50551, F7) A B E F G 1 No. States Rand No. Random Sample population 50 2 1 ALABAMA 0.5296685 NEW HAMPSHIRE sample 10 3 2 ALASKA 0.4493186 OKLAHOMA k 5 4 3 ARIZONA 0.707914 KANSAS 5 4 ARKANSAS 0.4831379 NORTH DAKOTA 6 5 CALIFORNIA 0.7277162 INDIANA Random Sample Sample Name 7 6 COLORADO 0.5865002 MISSISSIPPI 8 7:ONNECTICU 0.7640596 ILLINOIS 9 8 DELAWARE 0.5783029 MISSOURI 525 10 15 INDIANA MARYLAND COLORADOarrow_forwardSuppose the Internal Revenue Service reported that the mean tax refund for the year 2022 was $3401. Assume the standard deviation is $82.5 and that the amounts refunded follow a normal probability distribution. Solve the following three parts? (For the answer to question 14, 15, and 16, start with making a bell curve. Identify on the bell curve where is mean, X, and area(s) to be determined. 1.What percent of the refunds are more than $3,500? 2. What percent of the refunds are more than $3500 but less than $3579? 3. What percent of the refunds are more than $3325 but less than $3579?arrow_forward
- A normal distribution has a mean of 50 and a standard deviation of 4. Solve the following three parts? 1. Compute the probability of a value between 44.0 and 55.0. (The question requires finding probability value between 44 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 44, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the answer of the second part.) 2. Compute the probability of a value greater than 55.0. Use the same formula, x=55 and subtract the answer from 1. 3. Compute the probability of a value between 52.0 and 55.0. (The question requires finding probability value between 52 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 52, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the…arrow_forwardIf a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9. The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24? The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by a step by step creating a chart. Clearly mark the range, identifying the…arrow_forwardClient 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127arrow_forward
- Client 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127 a) Determine the mean change in patient weight from before to after the diet (after – before). What is the 95% confidence interval of this mean difference?arrow_forwardIn order to find probability, you can use this formula in Microsoft Excel: The best way to understand and solve these problems is by first drawing a bell curve and marking key points such as x, the mean, and the areas of interest. Once marked on the bell curve, figure out what calculations are needed to find the area of interest. =NORM.DIST(x, Mean, Standard Dev., TRUE). When the question mentions “greater than” you may have to subtract your answer from 1. When the question mentions “between (two values)”, you need to do separate calculation for both values and then subtract their results to get the answer. 1. Compute the probability of a value between 44.0 and 55.0. (The question requires finding probability value between 44 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 44, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the…arrow_forwardIf a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9. The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24? The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by creating a chart. Clearly mark the range, identifying the lower and upper…arrow_forward
- Problem 1: The mean hourly pay of an American Airlines flight attendant is normally distributed with a mean of 40 per hour and a standard deviation of 3.00 per hour. What is the probability that the hourly pay of a randomly selected flight attendant is: Between the mean and $45 per hour? More than $45 per hour? Less than $32 per hour? Problem 2: The mean of a normal probability distribution is 400 pounds. The standard deviation is 10 pounds. What is the area between 415 pounds and the mean of 400 pounds? What is the area between the mean and 395 pounds? What is the probability of randomly selecting a value less than 395 pounds? Problem 3: In New York State, the mean salary for high school teachers in 2022 was 81,410 with a standard deviation of 9,500. Only Alaska’s mean salary was higher. Assume New York’s state salaries follow a normal distribution. What percent of New York State high school teachers earn between 70,000 and 75,000? What percent of New York State high school…arrow_forwardPls help asaparrow_forwardSolve the following LP problem using the Extreme Point Theorem: Subject to: Maximize Z-6+4y 2+y≤8 2x + y ≤10 2,y20 Solve it using the graphical method. Guidelines for preparation for the teacher's questions: Understand the basics of Linear Programming (LP) 1. Know how to formulate an LP model. 2. Be able to identify decision variables, objective functions, and constraints. Be comfortable with graphical solutions 3. Know how to plot feasible regions and find extreme points. 4. Understand how constraints affect the solution space. Understand the Extreme Point Theorem 5. Know why solutions always occur at extreme points. 6. Be able to explain how optimization changes with different constraints. Think about real-world implications 7. Consider how removing or modifying constraints affects the solution. 8. Be prepared to explain why LP problems are used in business, economics, and operations research.arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





