
International Edition---engineering Mechanics: Statics 4th Edition
4th Edition
ISBN: 9781305856240
Author: Pytel
Publisher: Cengage
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 8, Problem 8.88P
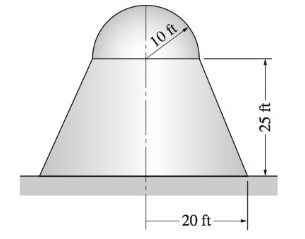
Compute the surface area of the axi-symmetric domed structure.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
practise question
Can you provide steps and an explaination on how the height value to calculate the Pressure at point B is (-5-3.5) and the solution is 86.4kPa.
PROBLEM 3.46
The solid cylindrical rod BC of length L = 600
mm is attached to the rigid lever AB of length a
= 380 mm and to the support at C. When a 500
N force P is applied at A, design specifications
require that the displacement of A not exceed
25 mm when a 500 N force P is applied at A
For the material indicated determine the
required diameter of the rod.
Aluminium: Tall = 65 MPa, G = 27 GPa.
A
Chapter 8 Solutions
International Edition---engineering Mechanics: Statics 4th Edition
Ch. 8 - Use integration to determine the coordinates of...Ch. 8 - Use integration to determine the coordinates of...Ch. 8 - Use integration to determine the coordinates of...Ch. 8 - Use integration to determine the coordinates of...Ch. 8 - Use integration to determine the coordinates of...Ch. 8 - Use integration to determine the coordinates of...Ch. 8 - Using integration, locate the centroid of the area...Ch. 8 - Determine the y-coordinate of the centroid of the...Ch. 8 - Determine the y-coordinate 0f the centroid of the...Ch. 8 - Use integration to locate the centroid of the...
Ch. 8 - Locate the centroid of the parabola by...Ch. 8 - Use integration to locate the centroid of the...Ch. 8 - The parametric equations of the plane curve known...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - Use the method of composite areas to calculate the...Ch. 8 - The plane region is bounded by a semicircle of...Ch. 8 - The centroid of the plane region shown is at C....Ch. 8 - Compute the centroidal coordinates of the L-shaped...Ch. 8 - Find the centroidal coordinates of the plane...Ch. 8 - Using the method of composite areas, find the...Ch. 8 - Given that the centroid of the plane region is at...Ch. 8 - Using the method of composite curves, locate the...Ch. 8 - Using the method of composite curves, locate the...Ch. 8 - Using the method of composite curves, locate the...Ch. 8 - Using the method of composite curves, locate the...Ch. 8 - Using the method of composite curves, locate the...Ch. 8 - Using the method of composite curves, locate the...Ch. 8 - Determine the ratio a/b for which the centroid of...Ch. 8 - Use numerical integration to locate the centroid...Ch. 8 - Determine the centroidal coordinates of the plane...Ch. 8 - Compute the centroidal y-coordinate of the plane...Ch. 8 - The equation of the catenary shown is y = 100 cosh...Ch. 8 - Use integration to locate the centroid of the...Ch. 8 - By integration, find the centroid of the surface...Ch. 8 - Locate the centroid of the volume obtained by...Ch. 8 - Solve Prob. 8.41 assuming that the triangle is...Ch. 8 - Use integration to find the centroidal coordinates...Ch. 8 - Solve Prob. 8.43 assuming that the area is...Ch. 8 - Verify the centroidal z-coordinate of the pyramid...Ch. 8 - Use integration to compute the z-coordinate of the...Ch. 8 - Determine the centroidal z-coordinate of the...Ch. 8 - Prob. 8.48PCh. 8 - Locate the centroid of the volume between the...Ch. 8 - Prob. 8.50PCh. 8 - Prob. 8.51PCh. 8 - By the method of composite volumes, determine the...Ch. 8 - By the method of composite volumes, determine the...Ch. 8 - By the method of composite volumes, determine the...Ch. 8 - By the method of composite volumes, determine the...Ch. 8 - By the method of composite volumes, determine the...Ch. 8 - By the method of composite volumes, determine the...Ch. 8 - Use the method of composite volumes to determine...Ch. 8 - The cylindrical container will have maximum...Ch. 8 - Using the method of composite surfaces, locate the...Ch. 8 - Using the method of composite surfaces, locate the...Ch. 8 - Using the method of composite surfaces, locate the...Ch. 8 - Using the method of composite surfaces, locate the...Ch. 8 - Using the method of composite surfaces, locate the...Ch. 8 - Using the method of composite surfaces, locate the...Ch. 8 - The picture board and its triangular supporting...Ch. 8 - By the method of composite curves, locate the...Ch. 8 - By the method of composite curves, locate the...Ch. 8 - By the method of composite curves, locate the...Ch. 8 - Use numerical integration to find the centroid of...Ch. 8 - Prob. 8.71PCh. 8 - Locate the centroid of the volume generated by...Ch. 8 - Prob. 8.73PCh. 8 - Prob. 8.74PCh. 8 - Prob. 8.75PCh. 8 - A 6-in. diameter hole is drilled in the conical...Ch. 8 - A torus is formed by rotating the circle about the...Ch. 8 - A solid of revolution is formed by rotating the...Ch. 8 - Compute the volume of the spherical cap that is...Ch. 8 - Calculate the surface area of the truncated sphere...Ch. 8 - The rim of a steel V-belt pulley is formed by...Ch. 8 - Determine the volume of the machine part shown.Ch. 8 - A solid is generated by rotating the plane area...Ch. 8 - Prob. 8.84PCh. 8 - Find the surface area of the 90 duct elbow.Ch. 8 - Determine the volume of the concrete arch dam.Ch. 8 - (a) Find the volume of liquid contained in the...Ch. 8 - Compute the surface area of the axi-symmetric...Ch. 8 - The steel cylinder with a cylindrical hole is...Ch. 8 - The hemispherical glass bowl is filled with water....Ch. 8 - What is the ratio L/R for which the uniform wire...Ch. 8 - Small screws are used to fasten a piece of...Ch. 8 - Prob. 8.93PCh. 8 - 3.94 The aluminum cylinder is attached to the...Ch. 8 - Prob. 8.95PCh. 8 - Prob. 8.96PCh. 8 - Prob. 8.97PCh. 8 - Locate the center of gravity of the hammer if the...Ch. 8 - Prob. 8.99PCh. 8 - The cylindrical water tank with R = 10 ft and H =...Ch. 8 - Prob. 8.101PCh. 8 - Five 34-in. diameter holes are to be drilled in a...Ch. 8 - Wind pressure acting on a cylinder can be...Ch. 8 - Prob. 8.104PCh. 8 - The pressure acting on the square plate varies as...Ch. 8 - Prob. 8.106PCh. 8 - Prob. 8.107PCh. 8 - If the intensity of the line loading is...Ch. 8 - Prob. 8.109PCh. 8 - The intensity of the line loading acting on a...Ch. 8 - Determine the resultant force or resultant couple...Ch. 8 - The inside surface of each thin shell carries a...Ch. 8 - Calculate the resultant force caused by the water...Ch. 8 - Determine the resultant force acting on the elbow...Ch. 8 - Determine the smallest distance I) that would...Ch. 8 - Each of the three gates has a constant width 1:...Ch. 8 - The concrete dam shown in cross section holds back...Ch. 8 - A concrete seawater dam is shown in cross section....Ch. 8 - Determine the force F required to pull up the...Ch. 8 - The normal pressure acting on the triangular plate...Ch. 8 - One side of the container has a 03-m square door...Ch. 8 - The 12-ft wide quarter-circular gate AB is hinged...Ch. 8 - The center of gravity of the plane wire figure is...Ch. 8 - The 10-m wide gate restrains water at a depth of 6...Ch. 8 - Find the resultant of the line load shown.Ch. 8 - Prob. 8.126RPCh. 8 - Determine the centroidal coordinates of the volume...Ch. 8 - Prob. 8.128RPCh. 8 - Prob. 8.129RPCh. 8 - Prob. 8.130RPCh. 8 - Using the method of composite areas, find the...Ch. 8 - Find the centroid of the truncated parabolic...Ch. 8 - Prob. 8.133RPCh. 8 - A solid of revolution is formed by rotating the...Ch. 8 - Two hemispherical shells of inner diameter 1 m are...Ch. 8 - Calculate the area of the surface generated when...Ch. 8 - Determine the resultant of the line loading, given...Ch. 8 - Determine the centroidal coordinates of the plane...Ch. 8 - The sheet metal trough has a uniform wall...Ch. 8 - The trough is filled with water (=62.4lb/ft3)....Ch. 8 - The thin-walled cylindrical can with a spherical...Ch. 8 - Find the location of the centroid of the shaded...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Find the equivalent mass of the rocker arm assembly with respect to the x coordinate. k₁ mi m2 k₁arrow_forward2. Figure below shows a U-tube manometer open at both ends and containing a column of liquid mercury of length l and specific weight y. Considering a small displacement x of the manometer meniscus from its equilibrium position (or datum), determine the equivalent spring constant associated with the restoring force. Datum Area, Aarrow_forward1. The consequences of a head-on collision of two automobiles can be studied by considering the impact of the automobile on a barrier, as shown in figure below. Construct a mathematical model (i.e., draw the diagram) by considering the masses of the automobile body, engine, transmission, and suspension and the elasticity of the bumpers, radiator, sheet metal body, driveline, and engine mounts.arrow_forward
- 3.) 15.40 – Collar B moves up at constant velocity vB = 1.5 m/s. Rod AB has length = 1.2 m. The incline is at angle = 25°. Compute an expression for the angular velocity of rod AB, ė and the velocity of end A of the rod (✓✓) as a function of v₂,1,0,0. Then compute numerical answers for ȧ & y_ with 0 = 50°.arrow_forward2.) 15.12 The assembly shown consists of the straight rod ABC which passes through and is welded to the grectangular plate DEFH. The assembly rotates about the axis AC with a constant angular velocity of 9 rad/s. Knowing that the motion when viewed from C is counterclockwise, determine the velocity and acceleration of corner F.arrow_forward500 Q3: The attachment shown in Fig.3 is made of 1040 HR. The static force is 30 kN. Specify the weldment (give the pattern, electrode number, type of weld, length of weld, and leg size). Fig. 3 All dimension in mm 30 kN 100 (10 Marks)arrow_forward
- (read image) (answer given)arrow_forwardA cylinder and a disk are used as pulleys, as shown in the figure. Using the data given in the figure, if a body of mass m = 3 kg is released from rest after falling a height h 1.5 m, find: a) The velocity of the body. b) The angular velocity of the disk. c) The number of revolutions the cylinder has made. T₁ F Rd = 0.2 m md = 2 kg T T₂1 Rc = 0.4 m mc = 5 kg ☐ m = 3 kgarrow_forward(read image) (answer given)arrow_forward
- 11-5. Compute all the dimensional changes for the steel bar when subjected to the loads shown. The proportional limit of the steel is 230 MPa. 265 kN 100 mm 600 kN 25 mm thickness X Z 600 kN 450 mm E=207×103 MPa; μ= 0.25 265 kNarrow_forwardT₁ F Rd = 0.2 m md = 2 kg T₂ Tz1 Rc = 0.4 m mc = 5 kg m = 3 kgarrow_forward2. Find a basis of solutions by the Frobenius method. Try to identify the series as expansions of known functions. (x + 2)²y" + (x + 2)y' - y = 0 ; Hint: Let: z = x+2arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Properties of Fluids: The Basics; Author: Swanson Flo;https://www.youtube.com/watch?v=TgD3nEO1iCA;License: Standard YouTube License, CC-BY
Fluid Mechanics-Lecture-1_Introduction & Basic Concepts; Author: OOkul - UPSC & SSC Exams;https://www.youtube.com/watch?v=6bZodDnmE0o;License: Standard Youtube License