
A simple beam with a rectangular cross section (width, 3,5 inL; height, 12 in,) carries a trapczoi-dally distributed load of 1400 lb/ft at A and 1000 lb/ft at B on a span of 14 ft (sec figure).
Find the principal stresses
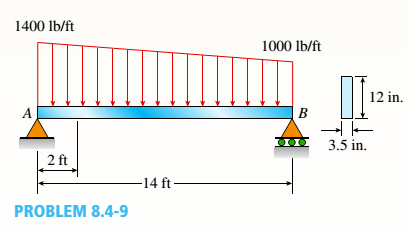
(a).
To find: Values of principal stress and maximum shear stress at neutral axis.
Answer to Problem 8.4.9P
Principal stress:
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Dimensions of beam,
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
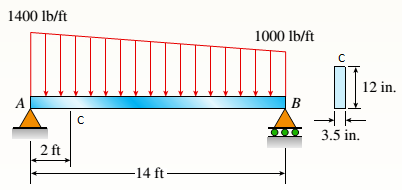
Load at point
From equilibrium;
So, bending moment at point
Shear force at
Moment of inertia:
First moment of area above neutral axis.:
So, bending stress at neutral axis::
And shear stress at that point:
For this situation no stress in
Values of principal and normal stress are given by following equation:
Maximum shear stress:
Conclusion:
Hence, we get:
Principal stresses
Maximum shear stress
(b).
To find: Values of Principal stress and maximum shear stress at 2 in above neutral axis.
Answer to Problem 8.4.9P
Principal stress:
Maximum shear stress:
Explanation of Solution
Given Information:
Beam length
Dimensions of beam,
Concept Used:
Bending stress
Shear stress
Principal normal stresses
Maximum shear stress
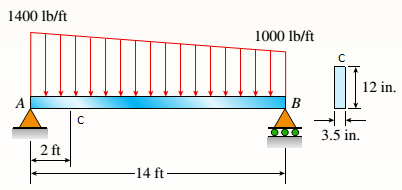
Load at point
From equilibrium:
So, bending moment at point
Shear force at
Moment of inertia:
First moment of area above given point:
So, bending stress at given point:
And shear stress at that point:
For this situation no stress in
Values of principal and normal stress are given by following equation:
Maximum shear stress ::
Conclusion:
Hence, we get;
Principal stresses
Maximum shear stress
(c).
To find: Values of principal stress and maximum shear stress at top of beam.
Answer to Problem 8.4.9P
Values of principal stress;
Maximum shear stress
Explanation of Solution
Given Information:
Beam length
Dimensions of beam,
Concept Used:
Bending stress
Shear stress
Values of principal stress are:
- Maximum shear stress:
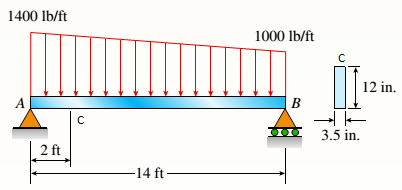
Load at point
From equilibrium:
So, bending moment at point
Moment of inertia:
First moment of area at the top of beam shall be zero,
So, bending stress at top::
And shear stress at that point:
For this situation no stress in
Values of principal and normal stress are given by following equation::
Maximum shear stress:
Conclusion:
Hence, we get:
Values of principal stress:
Maximum shear stress
Want to see more full solutions like this?
Chapter 8 Solutions
Mechanics of Materials, SI Edition
- My ID#016948724 please solve this problems and show me every step clear to follow pleasearrow_forwardMy ID# 016948724arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward
- Please do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward[Q2]: The cost information supplied by the cost accountant is as follows:Sales 20,00 units, $ 10 per unitCalculate the (a/ newsale guantity and (b) new selling price to earn the sameVariable cost $ 6 per unit, Fixed Cost $ 30,000, Profit $ 50,000profit ifi) Variable cost increases by $ 2 per unitil) Fixed cost increase by $ 10,000Ili) Variable cost increase by $ 1 per unit and fixed cost reduces by $ 10,000arrow_forward
- can you please help me perform Visual Inspection and Fractography of the attatched image: Preliminary examination to identify the fracture origin, suspected fatigue striation, and corrosion evidences.arrow_forwardcan you please help[ me conduct Causal Analysis (FTA) on the scenario attatched: FTA diagram which is a fault tree analysis diagram will be used to gain an overview of the entire path of failure from root cause to the top event (i.e., the swing’s detachment) and to identify interactions between misuse, material decay and inspection errors.arrow_forwardhi can you please help me in finding the stress intensity factor using a k-calcluator for the scenario attathced in the images.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
