
Concept explainers
Starting from rest, a 64.0-kg person bungee jumps from a tethered hot-air balloon 65.0 m above the ground. The bungee cord has negligible mass and unstretched length 25.8 m. One end is tied to the basket of the balloon and the other end to a harness around the person’s body. The cord is modeled as a spring that obeys Hooke’s law with a spring constant of 81.0 N/m, and the person’s body is modeled as a particle. The hot-air balloon does not move. (a) Express the gravitational potential energy of the person–Earth system as a function of the person’s variable height y above the ground. (b) Express the elastic potential energy of the cord as a function of y. (c) Express the total potential energy of the person–cord–Earth system as a function of y. (d) Plot a graph of the gravitational, elastic, and total potential energies as functions of y. (e) Assume air resistance is negligible. Determine the minimum height of the person above the ground during his plunge. (f) Docs the potential energy graph show any equilibrium position or positions? If so, at what elevations? Are they stable or unstable? (g) Determine the jumper’s maximum speed.
(a)
To show: The gravitational potential energy of the person–Earth system as a function of the person’s variable height
Answer to Problem 80CP
The gravitational potential energy of the person–Earth system as a function of the person’s variable height
Explanation of Solution
Given info: The mass of the person is
The acceleration due to gravity is
The expression for gravitational potential energy is as follows:
Here,
Substitute
Conclusion:
Therefore, the gravitational potential energy of the person–Earth system as a function of the person’s variable height
(b)
To show: Elastic potential energy of cord as a function of
Answer to Problem 80CP
The elastic potential energy of cord as a function of
Explanation of Solution
Given info: The mass of the person is
The expression for elastic potential energy of spring is as follows:
The cord will stretch by length x only when the person falls more than the length of the cord. Now, the height of the balloon h should be more than the length of the cord l plus the person’s height y, for safe landing.
The expression for extension in spring is as follows:
Here,
Substitute
Substitute
Conclusion:
Therefore, the elastic potential energy of the cord as function of
(c)
To show: The total potential energy of the person-cord–Earth system as a function of
Answer to Problem 80CP
The total potential energy of the person-cord–Earth system as a function of
Explanation of Solution
Given info: The mass of the person is
The expression for total potential energy of the person-cord–Earth system is as follows:
Substitute
Conclusion:
Therefore, the total potential energy of the person-cord–Earth system as a function of
(d)
To draw: The graph of gravitational, elastic, and total potential energies as a function of
Answer to Problem 80CP
The graph of gravitational, elastic, and total potential energies as a function of
Explanation of Solution
Introduction:
The gravitational potential energy above the surface of the earth is directly proportional to the height of the object.
The elastic potential energy is proportional to the square of displacement.
The total potential energy is the sum of all the potential energies in the system.
Given info: The mass of the person is
From part (a), the expression for gravitational potential energy of person as a function of
Table for the above expression is shown below:
The graph of gravitational potential energy with displacement is shown below:

Figure(1)
From part (a), the expression for the elastic potential energy of cord as a function of
The value of elastic potential energy of the cord remains zero till the person does not fall
equal to the length of cord; therefore, the value of the above equation is zero for
Table for the above expression is shown below:
The graph of elastic potential energy with displacement is represented below:
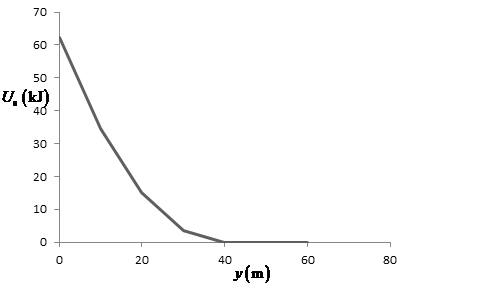
Figure(2)
From part (a), the expression for total potential energy of the person-cord–Earth system as a function of
When the value of
Table for the above expression is shown below:
The graph of total potential energy with displacement is represented below:
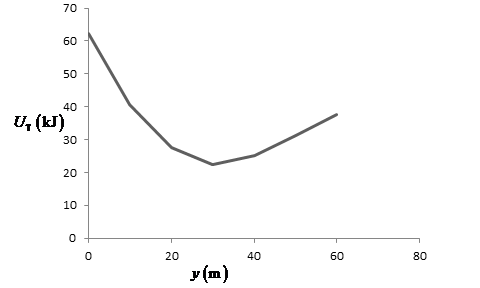
Figure(3)
(e)
The minimum height of the person above the ground during his plunge.
Answer to Problem 80CP
The minimum height of the person above the ground during his plunge is
Explanation of Solution
Given info: The mass of the person is
The expression for change in total energy is as follows:
Here,
The value of initial kinetic energy is zero, as the person is at rest.
The length of cord is
Substitute
At minimum height above the ground during plunge, the person comes to rest and the change in kinetic energy is zero, as both values of initial and final kinetic energies are zero.
Substitute
The expression for the roots of the above quadratic equation is as follows:
Substitute
Conclusion:
Therefore, the minimum height of the person above the ground during his plunge is
(f)
Whether potential energy graph shows any equilibrium position and if so the elevation of equilibrium position, whether the equilibrium points are stable or unstable.
Answer to Problem 80CP
The potential energy graph shows that in an equilibrium position at an elevation of
Explanation of Solution
Given info: The mass of the person is
The graph of potential energy shows the equilibrium position at the place where the value of total potential energy is minimum.
The expression for total potential energy is as follows:
Derive the above equation with the height of the person.
For the expression of minima, equate the above expression equal to zero.
The elevation at the point of equilibrium is
The person could not stop at the elevation of equilibrium position as he has kinetic energy that does not allow the person to stay at the elevation of equilibrium position. The equilibrium position is unstable.
Conclusion:
Therefore, the potential energy graph shows that in an equilibrium position at an elevation of
(g)
The jumper’s maximum speed.
Answer to Problem 80CP
The jumper’s maximum speed is
Explanation of Solution
Given info: The mass of the person is
The expression for change in total energy is as follows:
Substitute
The initial kinetic energy of the jumper is zero; hence, the change in the kinetic energy equals the kinetic energy at that position. Velocity is directly proportional to the square root of the kinetic energy; therefore, for maximum value of kinetic energy, the velocity is maximum.
Differentiate the above expression with respect to
Equate
Substitute
Substitute
The height at which the velocity is maximum is
Substitute
Substitute
Substitute
Conclusion:
Therefore, the jumper’s maximum speed is
Want to see more full solutions like this?
Chapter 8 Solutions
Bundle: Physics for Scientists and Engineers with Modern Physics, Loose-leaf Version, 9th + WebAssign Printed Access Card, Multi-Term
- please answer this asap!!!!arrow_forwardRT = 4.7E-30 18V IT = 2.3E-3A+ 12 38Ω ли 56Ω ли r5 27Ω ли r3 28Ω r4 > 75Ω r6 600 0.343V 75.8A Now figure out how much current in going through the r4 resistor. |4 = unit And then use that current to find the voltage drop across the r resistor. V4 = unitarrow_forward7 Find the volume inside the cone z² = x²+y², above the (x, y) plane, and between the spheres x²+y²+z² = 1 and x² + y²+z² = 4. Hint: use spherical polar coordinates.arrow_forward
- ганм Two long, straight wires are oriented perpendicular to the page, as shown in the figure(Figure 1). The current in one wire is I₁ = 3.0 A, pointing into the page, and the current in the other wire is 12 4.0 A, pointing out of the page. = Find the magnitude and direction of the net magnetic field at point P. Express your answer using two significant figures. VO ΜΕ ΑΣΦ ? Figure P 5.0 cm 5.0 cm ₁ = 3.0 A 12 = 4.0 A B: μΤ You have already submitted this answer. Enter a new answer. No credit lost. Try again. Submit Previous Answers Request Answer 1 of 1 Part B X Express your answer using two significant figures. ΜΕ ΑΣΦ 0 = 0 ? below the dashed line to the right P You have already submitted this answer. Enter a new answer. No credit lost. Try again.arrow_forwardAn infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of −2λ and radius r1, as shown in the figure. What is σinner, the surface charge density (charge per unit area) on the inner surface of the conducting shell? What is σouter, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by −2λ.)arrow_forwardA small conducting spherical shell with inner radius aa and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d (Figure 1). The inner shell has total charge +2q, and the outer shell has charge −2q. What's the total charge on the inner surface of the small shell? What's the total charge on the outer surface of the small shell? What's the total charge on the inner surface of the large shell? What's the total charge on the outer surface of the large shell?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





