
Concept explainers
The switch in Fig. 8.70 is moved from A to B at t = 0 after being at A for a long time. This places the two capacitors in series, thus allowing equal and opposite dc voltages to be trapped on the capacitors. (a) Determine v1(0−), v2(0−), and vR(0−). (b) Find v1(0+), v2(0+), and vR(0+). (c) Determine the time constant of vR(t). (d) Find vR(t), t > 0. (e) Find i(t). (f) Find v1(t) and v2(t) from i(t) and the initial values. (g) Show that the stored energy at t = ∞ plus the total energy dissipated in the 20 kΩ resistor is equal to the energy stored in the capacitors at t = 0.
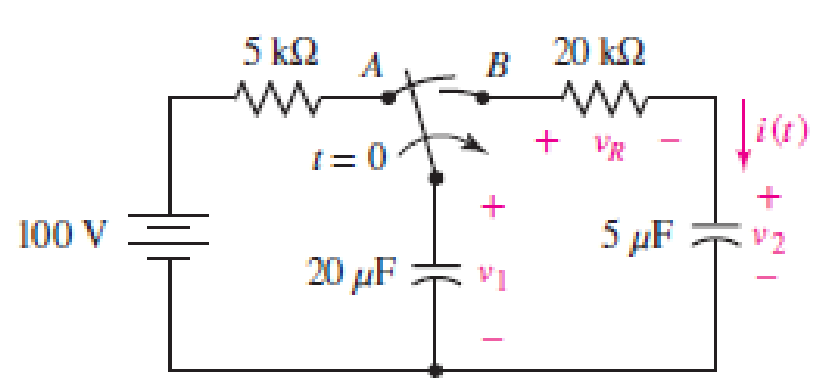
■ FIGURE 8.70
(a)
Find the value of
Answer to Problem 38E
The value of
Explanation of Solution
Given data:
Refer to Figure 8.70 in the textbook.
The switch is moved from
Calculation:
The given circuit is redrawn as shown in Figure 1.
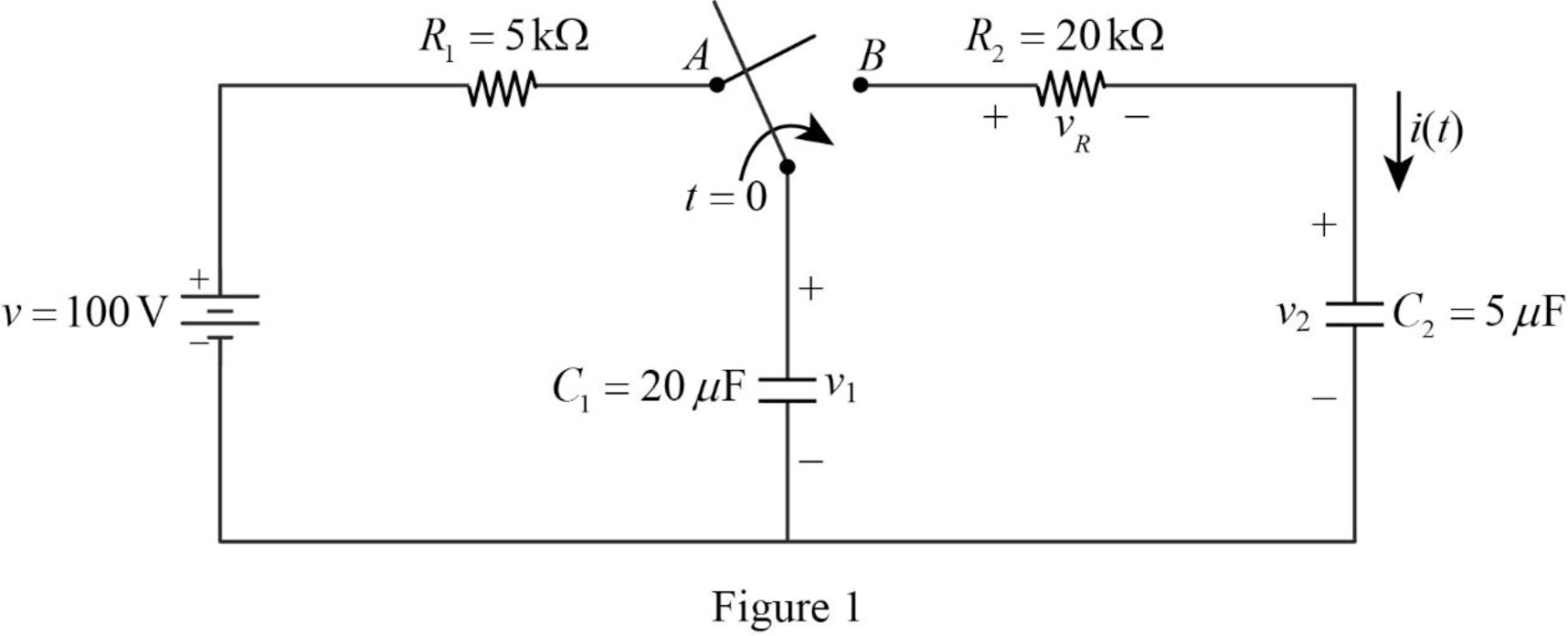
Refer to Figure 1, the voltage across the capacitor
For a DC circuit at steady state condition, when the switch is in position
Now, the Figure 1 is reduced as shown in Figure 2.
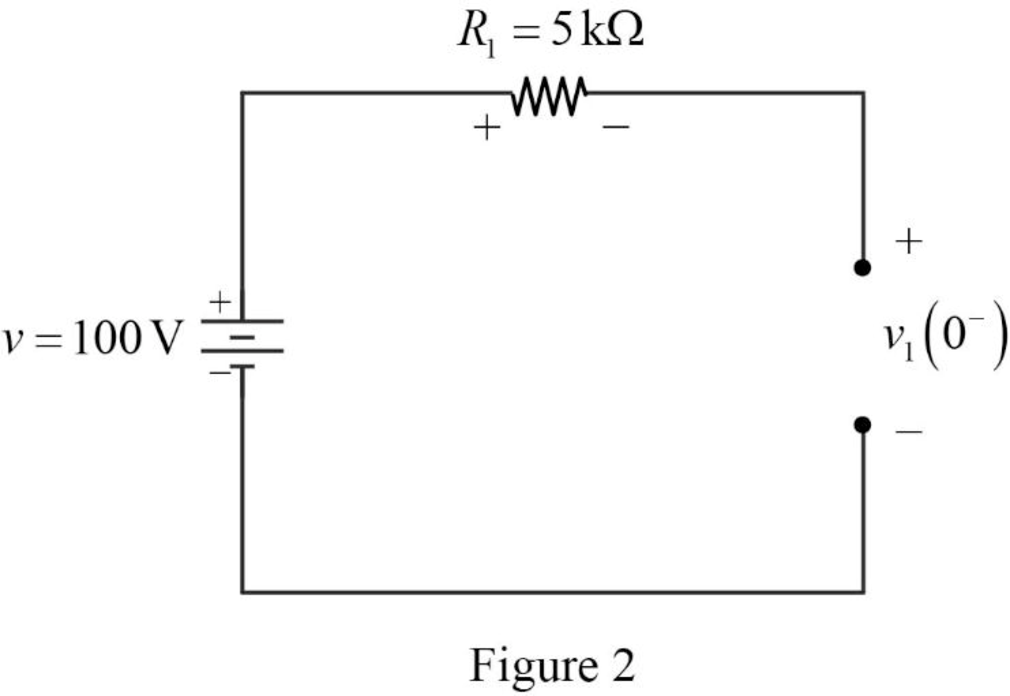
Refer to Figure 2, the voltage source
The voltage across the capacitor
Refer to Figure 2, the resistor
The voltage across the capacitor is always continuous so that,
Conclusion:
Thus, the value of
(b)
Find the value of
Answer to Problem 38E
The value of
Explanation of Solution
Calculation:
For time
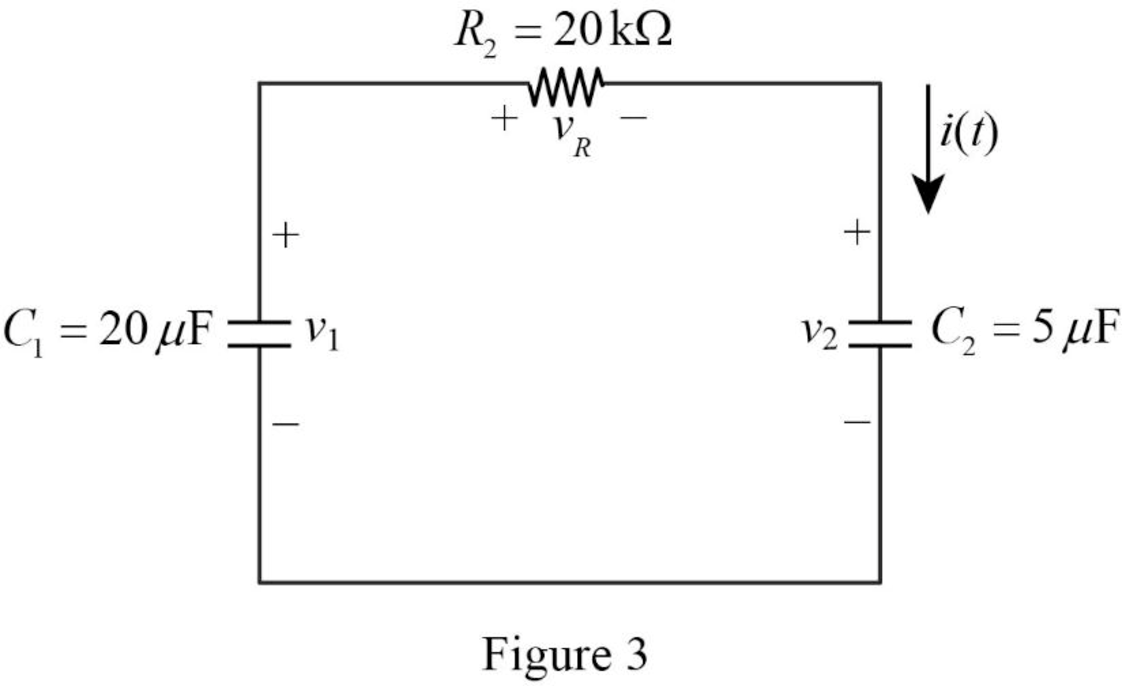
Refer to part (a),
Apply Kirchhoff’s voltage for the circuit shown in Figure 3 for time
Substitute
Conclusion:
Thus, the value of
(c)
Find the value of the time constant.
Answer to Problem 38E
The value of time constant
Explanation of Solution
Formula used:
Write a general expression to calculate the time constant.
Here,
Calculation:
Refer to Figure 3, the capacitors
The equivalent capacitance
Now, the Figure 3 is reduced as shown in Figure 4.
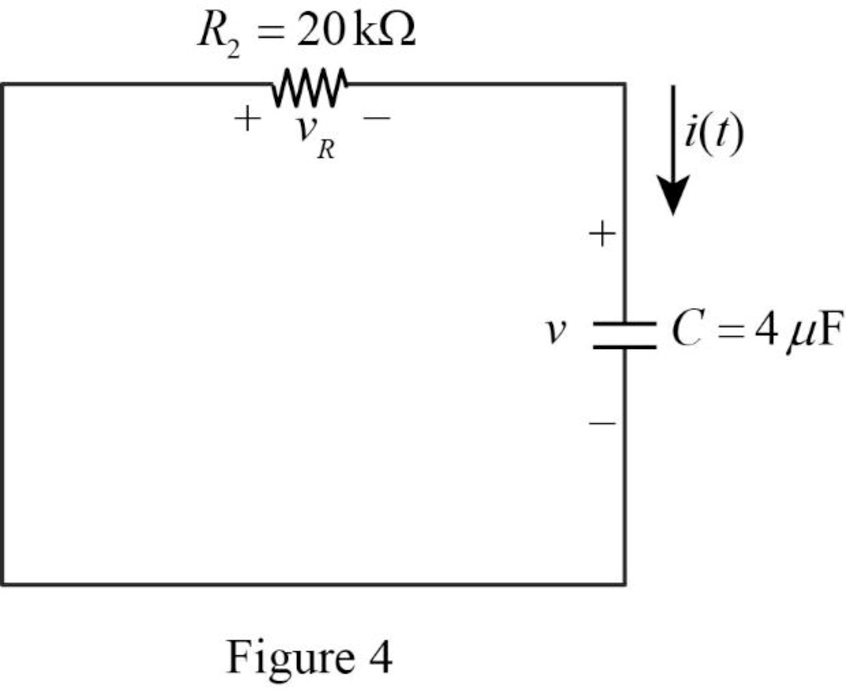
Refer to Figure 4, it shows the
Use equation (1) to find
Substitute
Conclusion:
Thus, the value of time constant
(d)
Find the expression of voltage
Answer to Problem 38E
The expression of voltage
Explanation of Solution
Formula used:
Write a general expression to calculate the voltage response of an
Here,
Refer to Figure 3, the resistor
Substitute
Substitute
Conclusion:
Thus, the expression of voltage
(e)
Find the expression of current
Answer to Problem 38E
The expression of current
Explanation of Solution
Calculation:
Refer to Figure 3, the capacitor
The current
Substitute
Conclusion:
Thus, the expression of current
(f)
Find the value of voltage
Answer to Problem 38E
The value of voltage
Explanation of Solution
Formula used:
Write a general expression to calculate the voltage across the capacitor.
Calculation:
From the given data, the capacitor
Use equation (1) to find the voltage
Substitute
Simplify the above equation to find
Use equation (1) to find the voltage
Substitute
Simplify the above equation to find
Conclusion:
Thus, the value of voltage
(g)
Show that the stored energy at
Explanation of Solution
Formula used:
Write a general expression to calculate the energy stored in a capacitor.
Write a general expression to calculate the energy stored in a resistor.
Here,
Calculation:
Refer to Figure 1, there are two capacitors placed in a circuit. Therefore, the total energy stored in a capacitor is,
Use equation (1) to find
Use equation (1) to find
Substitute equation (7) and (8) in (6).
Substitute
Substitute
Simplify the above equation to find
Refer to part (f),
Substitute
Refer to part (f),
Substitute
Substitute
Substitute
Simplify the above equation to find
Substitute
Simplify the above equation to find
Simplify the above equation to find
Substitute
Add
Therefore,
Therefore, the stored energy at
Conclusion:
Thus, the stored energy at
Want to see more full solutions like this?
Chapter 8 Solutions
Engineering Circuit Analysis
- Explain the advantages of three-phase supply for distribution purposes. (b) Assuming the relationship between the line and phase values of currents and voltages, show that the active power input to a three-phase balanced load is √3VI cos φ, where V and I are line quantities. (c) Three similar inductors, each of resistance 10 Ω and inductance 0.019 H, are delta-connected to a three-phase, 400 V, 50 Hz sinusoidal supply. Calcu late: the value of the line current; the power factor and the active power input to the circuit. ANS: 59.5 A, 0.858 lag, 35.5 kWarrow_forwardnot use ai pleasearrow_forwardA three-phase, 400 V, star-connected motor has an output of 50 kW, with an efficiency of 90 per cent and a power factor of 0.85. Calculate the line current. Sketch a phasor diagram showing the voltages and currents. If the motor windings were connected in mesh, what would be the correct voltage of a three phase supply suitable for the motor? ANS: 90.8 A, 240 Varrow_forward
- Don't use ai to answer I will report you answerarrow_forwardShow with the aid of a phasor diagram that for both star- and delta-connected balanced loads, the total active power is given by √3VI cos φ, where V and I are the line values of voltage and current respectively and φ is the angle between phase values of voltage and current. A balanced three-phase load consists of three coils, each of resistance 4 Ω and inductance 0.02 H. Determine the total active power when the coils are (a) star-connected, (b) delta-connected to a 400 V, three phase, 50 Hz supply. ANS:11.56 kW, 34.7 kWarrow_forwardThe load connected to a three-phase supply comprises three similar coils connected in star. The line currents are 25 A and the apparent and active power inputs are 20 kVA and 11 kW respectively. Find the line and phase voltages, reactive power input and the resistance and reactance of each coil. If the coils are now con nected in delta to the same three-phase supply, calculate the line currents and the active power taken. ANS : 462 V, 267 V, 16.7 kvar, 5.87 Ω, 8.92 Ω; 75 A, 33 kWarrow_forward
- A three-phase delta-connected load, each phase of which has an inductive reactance of 40 Ω and a resistance of 25 Ω, is fed from the secondary of a three-phase star-connected transformer which has a phase voltage of 230 V. Draw the circuit diagram of the system and calculate: (a) the current in each phase of the load; (b) the p.d. across each phase of the load; (c) the current in the transformer secondary windings; the total active power taken from the supply and its power factor.arrow_forwardDerive the numerical relationship between the line and phase currents for a balanced three-phase delta connected load. Three coils are connected in delta to a three-phase, three-wire, 400 V, 50 Hz supply and take a line current of 5 A 0.8 power factor lagging. Calculate the resistance and inductance of the coils. If the coils are star-connected to the same supply, calculate the line current and the total power. Calculate the line cur rents if one coil becomes open-circuited when the coils are connected in star. Ans: 110.7 Ω, 0.264 H; 1.67 A, 926 W; 1.445 A, 1.445 A, 0arrow_forwardDerive, for both star- and delta-connected systems, an expression for the total power input for a balanced three-phase load in terms of line voltage, line current and power factor. The star-connected secondary of a transformer supplies a delta-connected motor taking a power of 90 kW at a lagging power factor of 0.9. If the volt age between lines is 600 V, calculate the current in the transformer winding and in the motor winding. Draw circuit and phasor diagrams, properly labelled, showing all voltages and currents in the transformer secondary and the motor. ANS: . 96.2 A, 55.6 Aarrow_forward
- Deduce the relationship between the phase and the line voltages of a three-phase star-connected generator. If the phase voltage of a three-phase star-connected generator is 200 V, what will be the line voltages: (a) when the phases are correctly connected; (b) when the connections to one of the phases are reversed? ans: 346 V; 346 V, 200 V, 200 Varrow_forwardQ2: Given a discrete sequence x(n) = [1,-1,2,4, 1, 3,-1,1] and its spectrum X(k): i. Show that: X(k) =G(k)+WH(k) k=0,1,2,3,4,5,6,7 where G(k) = DFT[g(n)] and H(k) = DFT[h(n)], g(n) and h(n) are even and odd components of x(n) respectively. ii. Compute G(k) and H(k) using the method of computation of DFTS of two real sequences. (15 marks)arrow_forwardQ2: Given a discrete sequence x(n) = [1,-1,2,4, 1, 3,-1,1] and its spectrum X(k): i. Show that: X(k) = G(k)+WH(k) k = 0,1,2,3,4,5,6,7 where G(k) = DFT[g(n)] and H(k) = DFT[h(n)], g(n) and h(n) are even and odd components of x(n) respectively. ii. Compute G(k) and H(k) using the method of computation of DFTS of two real sequences.arrow_forward
 Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
