Videos
For the digraph shown in Fig. 8-25, find
a. the indegree and outdegree of A.
b. the indegree and outdegree of B.
c. the indegree and outdegree of D.
d. the sum of the indegrees of all the vertices.
e. the sum of the outdegrees of all the vertices.
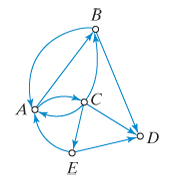
Figure 8-25
(a)
To find:
The in degree and out degree of A in the given digraph.
Answer to Problem 1E
Solution:
The in degree of A is 3 and out degree of A is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (1).
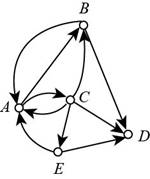
Figure (1)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (1) it can be noticed that there are 3 arcs having their ending vertex as A and 2 arcs having their starting vertex as A.
So, the indegree of A is 3 and outdegree of A is 2.
Conclusion:
Thus, the indegree of A is 3 and outdegree of A is 2.
(b)
To find:
The in degree and out degree of B in the given digraph.
Answer to Problem 1E
Solution:
The in degree of B is 2 and out degree of B is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (2).
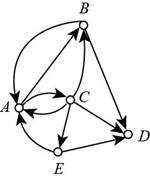
Figure (2)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (2) it can be noticed that there are 2 arcs having their ending vertex as B and 2 arcs having their starting vertex as B.
So, the indegree of B is 2 and outdegree of A is 2.
Conclusion:
Thus, the indegree of B is 2 and outdegree of B is 2.
(c)
To find:
The in degree and out degree of D in the given digraph.
Answer to Problem 1E
Solution:
The in degree of D is 3 and out degree of D is 0.
Explanation of Solution
Given:
The given digraph is shown in figure (3).
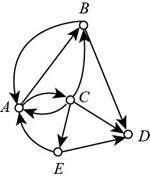
Figure (3)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (3) it can be noticed that there are 3 arcs having their ending vertex as D and no arc having their starting vertex as D.
So, the indegree of D is 3 and outdegree of D is 0.
Conclusion:
Thus, the indegree of D is 3 and outdegree of D is 0.
(d)
To find:
The sum of the in degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the indegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (4).
Figure (4)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (4) it can be noticed that there total 10 arcs, so there will be total 10 indegrees for all the vertices.
Conclusion:
Thus, the sum of all the indegrees is 10.
(e)
To find:
The sum of the out degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the outdegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (5).
Figure (5)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (5) it can be noticed that there total 10 arcs, so there will be total 10 outdegrees for all the vertices.
Conclusion:
Thus, the sum of all the outdegrees is 10.
Want to see more full solutions like this?
Chapter 8 Solutions
Excursions in Modern Mathematics (9th Edition)
- Problem: The probability density function of a random variable is given by the exponential distribution Find the probability that f(x) = {0.55e-0.55 x 0 < x, O elsewhere} a. the time to observe a particle is more than 200 microseconds. b. the time to observe a particle is less than 10 microseconds.arrow_forwardHow to solve it explain it step by step pleasearrow_forwardNot use ai pleasearrow_forward
- 2.3 Vibration amplitude of a machine plotted against time shown in Fig. T2.3. is described by sin(0.8+) In(t + 2) x(t) = t + 0.5 Here, t is in seconds and x is in millimeters 0.6 0.4 0.2 ° -0.2 mmm -0.4 0 10 20 30 40 50 60 70 Time [s] Fig. T2.3: Machine vibration amplitude variation against time Obtain the vibration velocity as a function of time, x(t), if it is measured by a vibration velocity sensor.arrow_forwardO State Jordan's lemma. Calculate the following integrals using complex variable techniques. 2π do (i) 1+8 cos²0' I COS x dx x²-2x+5° Leave your answers in terms of real functions of real variables.arrow_forwardSketch to scale the orbit of Earth about the sun. Graph Icarus’ orbit on the same set of axesWhile the sun is the center of Earth’s orbit, it is a focus of Icarus’ orbit. There aretwo points of intersection on the graph. Based on the graph, what is the approximate distance between the two points of intersection (in AU)?arrow_forward
- Refer to page 138 of the shared file for the numerical methods problem. Use Newton's method to approximate the solution of the given nonlinear system of equations. Start with an initial guess provided in the problem and iterate for at least two steps. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Show the Jacobian matrix, iteration formulas, and each step of the computation.arrow_forwardUnknown to a medical researcher, 7 out of 24 patients have a heart problem that will result in death if they receive the test drug. 5 patients are randomly selected to receive the drug and the rest receive a placebo. What is the probability that less than 4 patients will die? Express as a fraction or a decimal number rounded to four decimal places.arrow_forwardRefer to page 128 for the heat equation problem. Solve the one-dimensional heat equation with the given initial and boundary conditions. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Use Fourier series or other appropriate methods.arrow_forward
- Go to page 137 for the real analysis problem. Determine whether the given infinite series converges or diverges using appropriate convergence tests, such as the ratio test, root test, or comparison test. Justify your choice of test and provide clear steps. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Explain your reasoning and show all calculations.arrow_forwardRefer to page 132 of the document for the linear algebra problem. Solve the given nonhomogeneous system of equations using Gaussian elimination or matrix inverses, and express the general solution in parametric form. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Justify each step in the elimination process and interpret the solution.arrow_forwardTum to page 134 for the vector calculus problem. Verify Stokes' theorem by calculating the surface integral of the curl of a vector field over the given surface S and comparing it to the line integral of the same field over the boundary curve C. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyej KEMg1t2q15dbpVLCS/view? usp=sharing] Provide all detailed steps for calculating the curl, surface integral, and line integral.arrow_forward
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell