
Concept explainers
The compound hexaazaisowurtzitane is one of the highest-energy explosives known (C & E News, Jan. 17, 1994, p. 26). The compound, also known as CL-20, was first synthesized in 1987. The method of synthesis and detailed performance data are still classified because of CL-20’s potential military application in rocket boosters and in warheads of “smart” weapons. The structure of CL-20 is
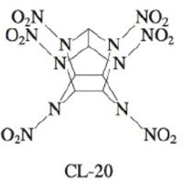
In such shorthand structures, each point where lines meet represents a carbon atom. In addition, the hydrogens attached to the carbon atoms are omitted; each of the six carbon atoms has one hydrogen atom attached. Finally, assume that the two O atoms in the NO2 groups are attached to N with one single bond and one double bond.
Three possible reactions for the explosive decomposition ofCL-20 are
i.
ii. C6H6N12O12(s) → 3CO(g) + 3CO2(g) + 6N2(g) + 3H2O(g)
iii. C6H6N12O12(s) → 6CO2(g) + 6N2(g) + 3H2 (g)
a. Use bond energies to estimate ∆E for these three reactions.
b. Which of the above reactions releases the largest amount of energy per kilogram of CL-20?
(a) (i)
Interpretation: The change in energy for the given chemical reactions has to be calculated.
Concept introduction: In a chemical reaction, energy is either gained, endothermic reactions, or released, exothermic reactions. The change in energy can be stated as the difference between the energy required to break the bonds in case of reactants and the energy released on the formation of the products.
To determine: The change in energy for the stated reactions.
Answer to Problem 163CP
The change in energy
Explanation of Solution
Given
The chemical reaction involved is,
Formula
Energy for reactants,
The total energy
For products,
The total energy
The change in energy
(ii)
Interpretation: The change in energy for the given chemical reactions has to be calculated.
Concept introduction: In a chemical reaction, energy is either gained, endothermic reactions, or released, exothermic reactions. The change in energy can be stated as the difference between the energy required to break the bonds in case of reactants and the energy released on the formation of the products.
To determine: The change in energy for the stated reactions.
Answer to Problem 163CP
The change in energy
Explanation of Solution
Given
The chemical reaction involved is,
Formula
Energy for reactants,
The total energy
For products,
The total energy
The change in energy
(iii)
Interpretation: The change in energy for the given chemical reactions has to be calculated.
Concept introduction: In a chemical reaction, energy is either gained, endothermic reactions, or released, exothermic reactions. The change in energy can be stated as the difference between the energy required to break the bonds in case of reactants and the energy released on the formation of the products.
To determine: The change in energy for the stated reactions.
Answer to Problem 163CP
The change in energy
Explanation of Solution
Given
The chemical reaction involved is,
Formula
Energy for reactants,
The total energy
For products,
The total energy
The change in energy
The change in energy can be stated as the difference between the energy required to break the bonds in case of reactants and the energy released on the formation of the products.
(b)
Interpretation: The change in energy for the given chemical reactions has to be calculated.
Concept introduction: In a chemical reaction, energy is either gained, endothermic reactions, or released, exothermic reactions. The change in energy can be stated as the difference between the energy required to break the bonds in case of reactants and the energy released on the formation of the products.
To determine: The reaction that releases the larger amount of energy per kilogram of
Answer to Problem 163CP
The reaction (iii) releases the largest amount of energy per kilogram of
Explanation of Solution
One mole of
In case of the (i) reaction,
Hence,
In case of the (ii) reaction,
Hence,
In case of the (iii) reaction,
Hence,
The reaction (iii) releases the largest amount of energy per kilogram of
The third stated reaction releases the largest amount of energy per kilogram of
Want to see more full solutions like this?
Chapter 8 Solutions
Chemistry
- Select the product for the following reaction. HO HO PCC OH ○ OH O HO ○ HO HO HOarrow_forward5:45 Х Select the final product for the following reaction sequence. O O 1. Mg. ether 2.D.Oarrow_forwardBased on the chart Two similarities between the molecule with alpha glycosidic linkages. Two similarities between the molecules with beta glycosidtic linkages. Two differences between the alpha and beta glycosidic linkages.arrow_forward
- please help fill in the tablearrow_forwardAnswer F pleasearrow_forward4. Refer to the data below to answer the following questions: The octapeptide saralasin is a specific antagonist of angiotensin II. A derivative of saralasin is used therapeutically as an antihypertensive. Amino acid analysis of saralasin show the presence of the following amino acids: Ala, Arg, His, Pro, Sar, Tyr, Val, Val A.Sar is the abbreviation for sarcosine, N-methyl aminoethanoic acid. Draw the structure of sarcosine. B. N-Terminal analysis by the Edman method shows saralasin contains sarcosine at the N-terminus. Partial hydrolysis of saralasin with dilute hydrochloric acid yields the following fragments: Tyr-Val-His Sar-Arg-Val His-Pro-Ala Val-Tyr-Val Arg-Val-Tyr What is the structure of saralasin?arrow_forward
- What is the structure of the DNA backbone?arrow_forwardPLEASE PLEASE PLEASE use hand drawn structures when possarrow_forward. M 1- MATCH each of the following terms to a structure from the list below. There is only one correct structure for each term and structures may be used more than once. Place the letter of the structure in the blank to the left of the corresponding term. A. Sanger dideoxy method C. Watson-Crick B. GAUCGUAAA D. translation E. HOH2C OH OH G. transcription I. AUGGCUGAG 0 K. OPOH2C 0- OH N- H NH2 F. -OPOH2C 0- OH OH H. Maxam-Gilbert method J. replication N L. HOH2C a. b. C. d. e. f. g. B M. AGATCGCTC a pyrimidine nucleoside RNA base sequence with guanine at the 3' end. DNA base sequence with cytosine at the 3' end. a purine nucleoside DNA sequencing method for the human genome 2'-deoxyadenosine 5'-phosphate process by which mRNA directs protein synthesis OH NH2arrow_forward
- Please use hand drawn structures when neededarrow_forwardB. Classify the following amino acid. Atoms other than carbon and hydrogen are labeled. a. acidic b. basic C. neutral C. Consider the following image. Which level of protein structure is shown here? a. primary b. secondary c. tertiary d. quaternary D. Consider the following image. H RH H HR H R HR HR RH Which level of protein structure is shown in the box? a. primary b. secondary R c. tertiary d. quaternary コー Rarrow_forwardBriefly answer three from the followings: a. What are the four structures of the protein? b. Why is the side chain (R) attached to the alpha carbon in the amino acids is important for the function? c. What are the types of amino acids? And how is it depend on the (R) structure? d. Write a reaction to prepare an amino acid. prodarrow_forward
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning General, Organic, and Biological ChemistryChemistryISBN:9781285853918Author:H. Stephen StokerPublisher:Cengage Learning
General, Organic, and Biological ChemistryChemistryISBN:9781285853918Author:H. Stephen StokerPublisher:Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning





