Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 7.CT, Problem 1CT
Draw and describe the locus of points in the plane that are equidistant from parallel lines l and m.
_________________________________________
________________________________________
Expert Solution & Answer
To determine
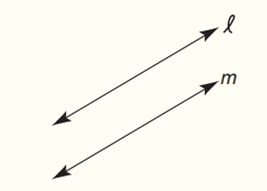
To draw and describe:
The locus of points in the plane that are equidistant from parallel lines l and m.
Answer to Problem 1CT
Solution:
The locus is in between both lines and is parallel to both.
Explanation of Solution
Definition:
A locus is set of all points and only those points that satisfy a given condition or set of conditions.
In must be noted that, the phrase “all points and only those points” has dual meaning as follows:
1. All points of the locus satisfy the given condition.
2. All points satisfying the given locus conditions are included in the locus.
Calculation:
A locus maintains an equal distance from each line.
Thus, we obtain that the locus must be half way between the two lines. In addition, since it maintains a constant distance, it must be parallel to both.
From this we came to know that the locus equidistant from two parallel lines l and m, is a line parallel to both l and m and halfway between them.
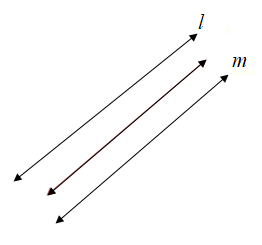
Conclusion:
The path formed by all points the same distance from two parallel lines will be one line halfway between the parallel lines.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Classwork for Geometry 1st X
S Savvas Realize
*
MARYIA DASHUTSINA-Ba
→ CA
savvasrealize.com/dashboard/classes/49ec9fc00d8f48ec9a4b05b30c9ee0ba
A > SIS © = =Wauconda Middle S...
31 WMS 8th Grade Tea... SIS Grades and Attenda....
esc
GEOMETRY 1ST
<
Study Guide T6
K
18
L
63°
9
N
M
Quadrilateral JKLM is a parallelogram. What is the m ZKJN?
mZKJN =
Review Progress
acer
Why is this proof incorrect? State what statement and/or reason is incorrect and why.
Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: Angle 3 is congruent to angle 5
Why is this proof incorrect?
Statements
Reasons
1. Overline OR is congruent to overline OQ, angle N is congruent to angle P
1. Given
2. Overline ON is congruent to overline OP
2. Converse of the Isosceles Triangle Theorem
3. Triangle ONR is congruent to triangle OPQ
3. SAS
4. Angle 3 is congruent to angle 5
4. CPCTC
Given: AABE ~ ACDE.
Prove: AC bisects BD.
Note: quadrilateral properties are not permitted in this proof.
Step
Statement
Reason
AABE ACDE
Given
2
ZDEC ZAEB
Vertical angles are congruent
try
Type of Statement
A
E
B
D
C
Chapter 7 Solutions
Elementary Geometry for College Students
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 3ECh. 7.1 - In Exercises 3 to 8, use the drawing provided....Ch. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 12ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 44ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 46ECh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - What is the general name of the point of...Ch. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Which lines or line segments or rays must be drawn...Ch. 7.2 - Is it really necessary to construct all three...Ch. 7.2 - Prob. 9ECh. 7.2 - a To locate the orthocenter, is it necessary to...Ch. 7.2 - To locate the centroid of a triangle, is it...Ch. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Must the centroid of an isosceles triangle lie on...Ch. 7.2 - Draw a triangle and, by construction, find its...Ch. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Draw an obtuse triangle and, by construction, find...Ch. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Is the incenter always located in the interior of...Ch. 7.2 - Prob. 23ECh. 7.2 - Find the length of the radius of the inscribed...Ch. 7.2 - Find the distance from the circumcenter to each...Ch. 7.2 - A triangle has angles measuring 30, 30, and 120....Ch. 7.2 - Given: Isosceles RST RS=RT=17andST=16. Medians RZ,...Ch. 7.2 - Given: Isosceles RST RS=RT=10andST=16. Medians RZ,...Ch. 7.2 - In MNP, medians MB, NA and PC intersect at...Ch. 7.2 - In MNP for Exercise 29, medians MB, NA and PC...Ch. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Does a rectangle have a an incenter? b a...Ch. 7.2 - Does a square have a an incenter? b a...Ch. 7.2 - Prob. 36ECh. 7.2 - Does a rhombus have a an incenter? b a...Ch. 7.2 - Does a isosceles trapezoid have a an incenter?.b a...Ch. 7.2 - A distributing company plans an Illinois location...Ch. 7.2 - There are plans to locate a disaster response...Ch. 7.2 - A circle is inscribed in an isosceles triangle...Ch. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.3 - Describe, if possible, how you would inscribe a...Ch. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 3ECh. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 5ECh. 7.3 - In Exercises 5 to 8, perform constructions....Ch. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Find the perimeter of a regular octagon if the...Ch. 7.3 - In a regular polygon with each side of length 6.5...Ch. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Prob. 15ECh. 7.3 - Find the lengths of the side and the radius of a...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Prob. 23ECh. 7.3 - Find the measure of each exterior angle of a...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Is there a regular polygon for which each central...Ch. 7.3 - Given regular hexagon ABCDEF with each side of...Ch. 7.3 - Given regular octagon RSTUVWXY with each side of...Ch. 7.3 - Given that RSTVQ is a regular pentagon and PQR is...Ch. 7.3 - Given: Regular pentagon RSTVQ with equilateral ...Ch. 7.3 - Given: Regular pentagon JKLMN not shown with...Ch. 7.3 - Is there a regular polygon with 8 diagonals? If...Ch. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Find the measure of a central angle of a regular...Ch. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 2CRCh. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 4CRCh. 7.CR - Prob. 5CRCh. 7.CR - Prob. 6CRCh. 7.CR - Prob. 7CRCh. 7.CR - Prob. 8CRCh. 7.CR - Prob. 9CRCh. 7.CR - Prob. 10CRCh. 7.CR - Prob. 11CRCh. 7.CR - Prob. 12CRCh. 7.CR - Prob. 13CRCh. 7.CR - Prob. 14CRCh. 7.CR - Prob. 15CRCh. 7.CR - Prob. 16CRCh. 7.CR - Prob. 17CRCh. 7.CR - Prob. 18CRCh. 7.CR - Prob. 19CRCh. 7.CR - Prob. 20CRCh. 7.CR - Prob. 21CRCh. 7.CR - Prob. 22CRCh. 7.CR - Prob. 23CRCh. 7.CR - Prob. 24CRCh. 7.CR - Prob. 25CRCh. 7.CR - Prob. 26CRCh. 7.CR - Prob. 27CRCh. 7.CR - In a regular polygon, each central angle measures...Ch. 7.CR - Prob. 29CRCh. 7.CR - Prob. 30CRCh. 7.CR - Can a circle be inscribed in each of the following...Ch. 7.CR - The length of the radius of a circle inscribed in...Ch. 7.CR - Prob. 33CRCh. 7.CR - Prob. 34CRCh. 7.CT - Draw and describe the locus of points in the plane...Ch. 7.CT - Prob. 2CTCh. 7.CT - Prob. 3CTCh. 7.CT - Prob. 4CTCh. 7.CT - Describe the locus of points in space that are at...Ch. 7.CT - Prob. 6CTCh. 7.CT - For a given triangle such as ABC, what word...Ch. 7.CT - Prob. 8CTCh. 7.CT - Which of the following must be concurrent at an...Ch. 7.CT - Classify as true/false: aA circle can be inscribed...Ch. 7.CT - Prob. 11CTCh. 7.CT - Prob. 12CTCh. 7.CT - Prob. 13CTCh. 7.CT - For a regular octagon, the length of the apothem...Ch. 7.CT - For a regular hexagon ABCDEF, the length of side...Ch. 7.CT - For rectangle MNPQ, points A, B, C and D are the...Ch. 7.CT - Prob. 17CT
Additional Math Textbook Solutions
Find more solutions based on key concepts
23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...
College Algebra (Collegiate Math)
The first derivative of function y=25x4.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
For each hour of class time, how many hours outside of class are recommended for studying and doing homework?
Elementary Algebra For College Students (10th Edition)
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
Fill in each blank so that the resulting statement is true.
1. The degree of the polynomial function is _____....
Algebra and Trigonometry (6th Edition)
Students in a Listening Responses class bought 40 tickets for a piano concert. The number of tickets purchased ...
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- 2) Based on the given information and the diagram, a. Which congruence statements can be proven? Select all that apply.Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: angle 3 is congruent to angle 5A. Overline ON is congruent to overline OPB. Angle 1 is congruent to angle 2C. Overline ON is congruent to overline OR and overline OP is congruent to overine OQD. angle 1 is congruent to angle 3 and angle 2 is congruent to angle 5There are more than one correct answerarrow_forwardnt/Ray Skew Lines/ J K # H L 艹 G C D E F Diagrams m Three Points th a Protractor Answer Attempt 3 out of 3 el 1 is congruent to Submit Answer 103 Log Out REE Young the → C # $arrow_forward4:54 PM Thu Jan 16 cdn.assess.prod.mheducation.com Question 3 The angle bisectors of APQR are PZ, QZ, and RZ. They meet at a single point Z. (In other words, Z is the incenter of APQR.) Suppose YZ = 22, QZ = 23, mz WPY 38°, and mzXQZ = 54°. Find the following measures. Note that the figure is not drawn to scale. P W Z X R Y mzXQW WZ = = 0 mz XRZ = 0°arrow_forward
- Ja дх dx dx Q3: Define the linear functional J: H()-R by تاریخ (v) = ½a(v, v) - (v) == Let u be the unique weak solution to a(u,v) = L(v) in H₁(2) and suppose that a(...) is a symmetric bilinear form on H() prove that a Buy v) = 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under J(u)=u' Au-ub, algebraic form Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer only 1-show that thelation to -Auf in N, u = 0 on a satisfies the stability Vulf and show that V(u-u,)||² = ||vu||2 - ||vu||2 lu-ulls Chu||2 2- Prove that Where =1 ||ul|= a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinear form a(u, v) = (Au, Av) + (Vu, Vv) + (Vu, v) + (u, v) Show that a(u, v) continues and V- elliptic on H(2) (3) (0.0), (3.0)arrow_forwardQ1: A) fill the following: 1- The number of triangular in a triangular region with 5 nodes is quadrilateral with n=5 and m=6 nodés is 2- The complex shape function in 1-D 3- dim(P4(K))=- (7M --- and in the and multiplex shape function in 2-D is 4- The trial space and test space for problem -Auf, u = go on and B) Define the energy norm and prove that the solution u, defined by Galerkin orthogonal satisfies the best approximation. Q2: A) Find the varitional form for the problem 1330 (b(x)) - x²=0, 0arrow_forwardcould you help?arrow_forward(ii)arrow_forwardA convex polygon is said to be regular if all of its sides have the same length and all angles between sides are the same. Let Pr denote the regular convex n-sided polygon. Thus, P3 is the equilateral triangle, P₁ is the square, P is the pentagon etc. Compute a formula for the size of any internal angle of Pn.arrow_forward+ Recall that a map, f: R2 R², is an isometry if |P-Q| = |ƒ(P) — ƒ (Q) for all pairs of points P and Q in R². Thus, f is a distance preserving map. Show that an isometry, f: R² → R² also preserves angles. In other words if two line segments meeting at a point determine an angle a, their image line segments meeting at the image of that point also determine the angle a.arrow_forwardUsing Harriott's formula for the area of a triangle on the unit sphere, S2, compute the Euler characteristic X(S2). Make sure to explain what the Euler characteristic is. (The point of the exercise is to show that this notion is well-defined.)arrow_forwardProve Harriot's Formula (Area of a Triangle on a Sphere).arrow_forwardIn rhombus ABCD, diagonals BD¯¯¯¯¯¯BD¯ and AC¯¯¯¯¯AC¯ intersect at point E. If BE = 4n – 3 and EC = 2n + 5, which expression can be used to represent AD?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY