Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7.1, Problem 8E
Note: Exercises preceded by an asterisk are of a more challenging nature.
In Exercises 3 to 8, use the drawing provided.
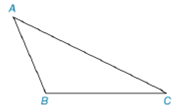
Given: Obtuse
Construct: The altitude from
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Answer number 15
Solve for 14
Solve for y
Chapter 7 Solutions
Elementary Geometry for College Students
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 3ECh. 7.1 - In Exercises 3 to 8, use the drawing provided....Ch. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 12ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 44ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 46ECh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - What is the general name of the point of...Ch. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Which lines or line segments or rays must be drawn...Ch. 7.2 - Is it really necessary to construct all three...Ch. 7.2 - Prob. 9ECh. 7.2 - a To locate the orthocenter, is it necessary to...Ch. 7.2 - To locate the centroid of a triangle, is it...Ch. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Must the centroid of an isosceles triangle lie on...Ch. 7.2 - Draw a triangle and, by construction, find its...Ch. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Draw an obtuse triangle and, by construction, find...Ch. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Is the incenter always located in the interior of...Ch. 7.2 - Prob. 23ECh. 7.2 - Find the length of the radius of the inscribed...Ch. 7.2 - Find the distance from the circumcenter to each...Ch. 7.2 - A triangle has angles measuring 30, 30, and 120....Ch. 7.2 - Given: Isosceles RST RS=RT=17andST=16. Medians RZ,...Ch. 7.2 - Given: Isosceles RST RS=RT=10andST=16. Medians RZ,...Ch. 7.2 - In MNP, medians MB, NA and PC intersect at...Ch. 7.2 - In MNP for Exercise 29, medians MB, NA and PC...Ch. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Does a rectangle have a an incenter? b a...Ch. 7.2 - Does a square have a an incenter? b a...Ch. 7.2 - Prob. 36ECh. 7.2 - Does a rhombus have a an incenter? b a...Ch. 7.2 - Does a isosceles trapezoid have a an incenter?.b a...Ch. 7.2 - A distributing company plans an Illinois location...Ch. 7.2 - There are plans to locate a disaster response...Ch. 7.2 - A circle is inscribed in an isosceles triangle...Ch. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.3 - Describe, if possible, how you would inscribe a...Ch. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 3ECh. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 5ECh. 7.3 - In Exercises 5 to 8, perform constructions....Ch. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Find the perimeter of a regular octagon if the...Ch. 7.3 - In a regular polygon with each side of length 6.5...Ch. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Prob. 15ECh. 7.3 - Find the lengths of the side and the radius of a...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Prob. 23ECh. 7.3 - Find the measure of each exterior angle of a...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Is there a regular polygon for which each central...Ch. 7.3 - Given regular hexagon ABCDEF with each side of...Ch. 7.3 - Given regular octagon RSTUVWXY with each side of...Ch. 7.3 - Given that RSTVQ is a regular pentagon and PQR is...Ch. 7.3 - Given: Regular pentagon RSTVQ with equilateral ...Ch. 7.3 - Given: Regular pentagon JKLMN not shown with...Ch. 7.3 - Is there a regular polygon with 8 diagonals? If...Ch. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Find the measure of a central angle of a regular...Ch. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 2CRCh. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 4CRCh. 7.CR - Prob. 5CRCh. 7.CR - Prob. 6CRCh. 7.CR - Prob. 7CRCh. 7.CR - Prob. 8CRCh. 7.CR - Prob. 9CRCh. 7.CR - Prob. 10CRCh. 7.CR - Prob. 11CRCh. 7.CR - Prob. 12CRCh. 7.CR - Prob. 13CRCh. 7.CR - Prob. 14CRCh. 7.CR - Prob. 15CRCh. 7.CR - Prob. 16CRCh. 7.CR - Prob. 17CRCh. 7.CR - Prob. 18CRCh. 7.CR - Prob. 19CRCh. 7.CR - Prob. 20CRCh. 7.CR - Prob. 21CRCh. 7.CR - Prob. 22CRCh. 7.CR - Prob. 23CRCh. 7.CR - Prob. 24CRCh. 7.CR - Prob. 25CRCh. 7.CR - Prob. 26CRCh. 7.CR - Prob. 27CRCh. 7.CR - In a regular polygon, each central angle measures...Ch. 7.CR - Prob. 29CRCh. 7.CR - Prob. 30CRCh. 7.CR - Can a circle be inscribed in each of the following...Ch. 7.CR - The length of the radius of a circle inscribed in...Ch. 7.CR - Prob. 33CRCh. 7.CR - Prob. 34CRCh. 7.CT - Draw and describe the locus of points in the plane...Ch. 7.CT - Prob. 2CTCh. 7.CT - Prob. 3CTCh. 7.CT - Prob. 4CTCh. 7.CT - Describe the locus of points in space that are at...Ch. 7.CT - Prob. 6CTCh. 7.CT - For a given triangle such as ABC, what word...Ch. 7.CT - Prob. 8CTCh. 7.CT - Which of the following must be concurrent at an...Ch. 7.CT - Classify as true/false: aA circle can be inscribed...Ch. 7.CT - Prob. 11CTCh. 7.CT - Prob. 12CTCh. 7.CT - Prob. 13CTCh. 7.CT - For a regular octagon, the length of the apothem...Ch. 7.CT - For a regular hexagon ABCDEF, the length of side...Ch. 7.CT - For rectangle MNPQ, points A, B, C and D are the...Ch. 7.CT - Prob. 17CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Solve for angle x and yarrow_forwardSolve for angle earrow_forwardUse the figure for Exercises 1-2. Suppose you use geometry software to construct a secant CE and tangent CD that intersect on a circle at point C. File Edit Display Construct Transform Measure Graph Window Help D 1. Suppose you measure /DCE and you measure CBE. Then you drag the points around the circle and measure the angle and arc three more times. What would you expect to find each time? Which theorem from the lesson would you be demonstrating? 2. When the measure of the intercepted arc is 180°, what is the measure of the angle? What does that tell you about the secant?arrow_forward
- A tournament is a complete directed graph, for each pair of vertices x, y either (x, y) is an arc or (y, x) is an arc. One can think of this as a round robin tournament, where the vertices represent teams, each pair plays exactly once, with the direction of the arc indicating which team wins. (a) Prove that every tournament has a direct Hamiltonian path. That is a labeling of the teams V1, V2,..., Un so that vi beats Vi+1. That is a labeling so that team 1 beats team 2, team 2 beats team 3, etc. (b) A digraph is strongly connected if there is a directed path from any vertex to any other vertex. Equivalently, there is no partition of the teams into groups A, B so that every team in A beats every team in B. Prove that every strongly connected tournament has a directed Hamiltonian cycle. Use this to show that for any team there is an ordering as in part (a) for which the given team is first. (c) A king in a tournament is a vertex such that there is a direct path of length at most 2 to any…arrow_forwardThe following is known. The complete graph K2t on an even number of vertices has a 1- factorization (equivalently, its edges can be colored with 2t - 1 colors so that the edges incident to each vertex are distinct). This implies that the complete graph K2t+1 on an odd number of vertices has a factorization into copies of tK2 + K₁ (a matching plus an isolated vertex). A group of 10 people wants to set up a 45 week tennis schedule playing doubles, each week, the players will form 5 pairs. One of the pairs will not play, the other 4 pairs will each play one doubles match, two of the pairs playing each other and the other two pairs playing each other. Set up a schedule with the following constraints: Each pair of players is a doubles team exactly 4 times; during those 4 matches they see each other player exactly once; no two doubles teams play each other more than once. (a) Find a schedule. Hint - think about breaking the 45 weeks into 9 blocks of 5 weeks. Use factorizations of complete…arrow_forward. The two person game of slither is played on a graph. Players 1 and 2 take turns, building a path in the graph. To start, Player 1 picks a vertex. Player 2 then picks an edge incident to the vertex. Then, starting with Player 1, players alternate turns, picking a vertex not already selected that is adjacent to one of the ends of the path created so far. The first player who cannot select a vertex loses. (This happens when all neighbors of the end vertices of the path are on the path.) Prove that Player 2 has a winning strategy if the graph has a perfect matching and Player 1 has a winning strategy if the graph does not have a perfect matching. In each case describe a strategy for the winning player that guarantees that they will always be able to select a vertex. The strategy will be based on using a maximum matching to decide the next choice, and will, for one of the cases involve using the fact that maximality means no augmenting paths. Warning, the game slither is often described…arrow_forward
- Let D be a directed graph, with loops allowed, for which the indegree at each vertex is at most k and the outdegree at each vertex is at most k. Prove that the arcs of D can be colored so that the arcs entering each vertex must have distinct colors and the arcs leaving each vertex have distinct colors. An arc entering a vertex may have the same color as an arc leaving it. It is probably easiest to make use of a known result about edge coloring. Think about splitting each vertex into an ‘in’ and ‘out’ part and consider what type of graph you get.arrow_forward10 20 30 y vernier protractor scales. 60 30 0 30 60 40 30 20 10 0 30 60 0 10. Write the complement of each of the following angles. a. 67° b. 17°41' 11. Write the supplement of each of the following angles. a.41° b.99°32' 30 60 C. 20 10 20 90 60 30 69 30 30 40 50 c. 54°47' 53" 0 30 60 c. 103°03'27" 12. Given: AB CD and EF GH. Determine the value of each angle, 21 through /10, to the nearer minute. A- 25 21 = 22 = 23 = 24 = 25 = 46= 27 = C 28 = 29 = 210 = E 26 22 210 81°00' 29 4 142°00' G H 94°40' B Darrow_forwardName: Tan Tong 16.5 Bonvicino - Period 5 1 Find the exact volume of a right hexagonal prism such that the base is a regular hexagon with a side length of 8 cm and whose distance between the two bases is 5 cm. Show all work. (4 pts) 83 tan 30°= Regular hexagon So length ~ 480 tango Cm Hexagon int angle =36016 8cm Angle bisec isper p bisect Side length 4 X=an 300 2 In the accompanying diagram of circle O, PA is tangent to the circle at A, PDC is a secant, diameter AEOC intersects chord BD at E, chords AB, BC, and DA are drawn, mDA = 46° and mBC is 32° more than mAB. If the radius of the circle is 8 cm, E is the midpoint of AO and the length of ED is 2 less than the length of BE, answer each of the following. Show all work. (a) marrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License