Chapter 7.6, Problem 99AE

Projectile Motion An object is propelled upward at an angle $\theta ,{\text{ 45}}^{\circ }\text{ < }\theta {\text{ < 90}}^{\circ }$, to the horizontal with an initial velocity $v_0$ feet per second from the base of a plane that makes an angle of ${45}^{\circ }$ with the horizontal. See the illustration. If air resistance is ignored, the distance $R$ that it travels up the inclined plane is given by the function

$R\left(\theta \right)\text{ = }\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right)$

Show that

$R\left(\theta \right)\text{ = }\frac{v_0^2\sqrt{2}}{32}[sin\left(2\theta \right)-cos\left(2\theta \right)-1]$

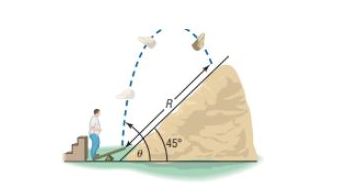
In calculus, you will be asked to find the angle $\theta$ that maximizes $R$ by solving the equation

$\sin \left(2\theta \right)\text{ + cos}\left(2\theta \right)\text{ = 0}$

solve the equation for $\theta$.

What is the maximum distance $R$ if $v_0\text{ =32}$ feet per second?

Graph $R\text{ = }R\left(\theta \right),{\text{ 45}}^{\circ }\le \theta \le {\text{ 90}}^{\circ }$, and find the angle $\theta$ that maximizes the distance $R$. Also find the maximum distance. Use $v_0\text{ = 32 }$ feet per second. Compare the results with the answers found in parts (b) and (c).