Chapter 7.6, Problem 63PPS

a.

To determine

To observe what happens when the given function is multiplied by a constant between 0 and 1.

Explanation of Solution

Given:

  $f(x)=b^x$

Calculation:

Let $f(x)=2^x$

Now multiply the given function with any value between 0 and 1, say $\frac{1}{3}$ .

  $\begin{array}{l}\Rightarrow g(x)=\frac{1}{3}f(x)\\ $ \Rightarrow g(x)=\frac{1}{3}{(2)}^x$\end{array}$

Calculation for graph:

Consider $f(x)=2^x$

Values of x	Values of f (x)
0	1
1	2
-1	0.5
2	4
-2	0.25

From the above table the graph can be plotted.

Calculation for graph:

Consider $g(x)=\frac{1}{3}{(2)}^x$

Values of x	Values of g (x)
0	0.33
1	0.67
-1	0.167
2	1.33
-2	0.833

From the above table the graph can be plotted.

Plotting both the graphs on the same plane:

  

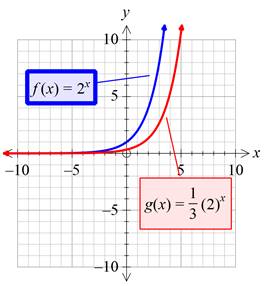
Interpretation:

By multiplying the given function with a value between 0 and 1, it is found that the new function becomes the non-rigid transform of the given function which is vertically shrink by a factor of the number multiplied to the given function, which is $\frac{1}{3}$ in this case.

b.

To determine

To describe the graph as the constant approaches 0

Explanation of Solution

Given:

  $f(x)=b^x$

Calculation:

Let $f(x)=2^x$

Now multiply the given function with any value between 0 and 1, say $\frac{1}{3}$ .

  $\begin{array}{l}\Rightarrow g(x)=\frac{1}{3}f(x)\\ $ \Rightarrow g(x)=\frac{1}{3}{(2)}^x$\end{array}$

Calculation for graph:

Consider $f(x)=2^x$

Values of x	Values of f (x)
0	1
1	2
-1	0.5
2	4
-2	0.25

From the above table the graph can be plotted.

Calculation for graph:

Consider $g(x)=\frac{1}{3}{(2)}^x$

Values of x	Values of g (x)
0	0.33
1	0.67
-1	0.167
2	1.33
-2	0.833

From the above table the graph can be plotted.

Plotting both the graphs on the same plane:

  

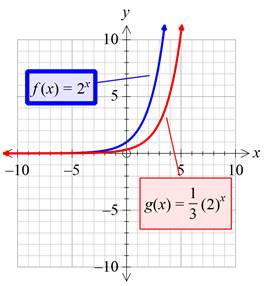
Interpretation:

By multiplying the given function with a value between 0 and 1, it is found that the new function becomes the non-rigid transform of the given function which is vertically shrink by a factor of the number multiplied to the given function, which is $\frac{1}{3}$ in this case.

So, as the value of the constant multiplied, the function decreases and approach to zero the curve and will tend to become flat and ultimately become flat as the value of constant multiplied tends to 0.

c.

To determine

To observe what happens when the given function is multiplied by a constant greater than 1.

Explanation of Solution

Given:

  $f(x)=b^x$

Calculation:

Let $f(x)=2^x$

Now multiply the given function with any value greater than 1, say 3.

  $\begin{array}{l}\Rightarrow g(x)=3f(x)\\ $ \Rightarrow g(x)=3{(2)}^x$\end{array}$

Calculation for graph:

Consider $f(x)=2^x$

Values of x	Values of f (x)
0	1
1	2
-1	0.5
2	4
-2	0.25

From the above table the graph can be plotted.

Calculation for graph:

Consider $g(x)=3{(2)}^x$

Values of x	Values of g (x)
0	3
1	6
-1	3
2	12
-2	0.75

From the above table the graph can be plotted.

Plotting both the graphs on the same plane:

  

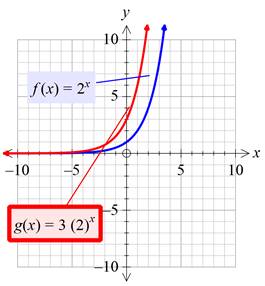
Interpretation:

By multiplying the given function with a value greater than 1, it is found that the new function becomes the non-rigid transform of the given function which is vertically stretched by a factor of the number multiplied to the given function, which is 3 in this case.

d.

To determine

To describe the graph as the constant approaches $\infty$ .

Explanation of Solution

Given:

  $f(x)=b^x$

Calculation:

Let $f(x)=2^x$

Now multiply the given function with any value between 0 and 1, say 3.

  $\begin{array}{l}\Rightarrow g(x)=3f(x)\\ $ \Rightarrow g(x)=3{(2)}^x$\end{array}$

Calculation for graph:

Consider $f(x)=2^x$

Values of x	Values of f (x)
0	1
1	2
-1	0.5
2	4
-2	0.25

From the above table the graph can be plotted.

Calculation for graph:

Consider $g(x)=3{(2)}^x$

Values of x	Values of g (x)
0	3
1	6
-1	3
2	12
-2	0.75

From the above table the graph can be plotted.

Plotting both the graphs on the same plane:

  

Interpretation:

By multiplying the given function with a greater value, it is found that the new function becomes the non-rigid transform of the given function which is vertically stretch by a factor of the number multiplied to the given function, which is 3 in this case.

So, as the value of the constant multiplied is increases and approach to $\infty$ the curve will tend to become flat.