Finite Mathematics, Loose-leaf Version
7th Edition
ISBN: 9781337291262
Author: Stefan Waner, Steven Costenoble
Publisher: Brooks Cole
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 7.4, Problem 37E
Elimination Tournaments The following diagram illustrates a 16-team tournament bracket, in which the 16 participating teams are arranged on the left under Round 1 and the winners of each round are added as the tournament progresses. The top team in each game is considered the “home” team, so the top-to-bottom order matters.
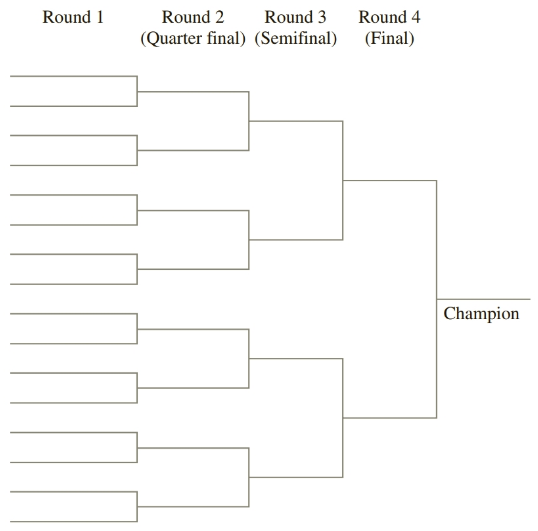
To seed a tournament means to select which teams to play each other in the first round according to their preliminary ranking. For instance, in professional tennis and NCAA basketball the seeding is set up in the following order based on the preliminary rankings: 1 versus 16, 8 versus 9, 5 versus 12, 4 versus 13, 6 versus 11, 3 versus 14, 7 versus 10, and 2 versus 15.48 Exercises 37–40 are based on various types of elimination tournaments. (Leave each answer as a formula.)
In a randomly chosen seeding of a 16-team tournament, what is the probability that the top-ranked team plays the bottom-ranked team, the second-ranked team plays the second-lowest ranked team, and so on? [HinT: See Exercise 65 in Section 7.4.]
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Solve the problems
the larger of two supplementary angles exceeds 7 times the smaller by 4°. Find the measure of the larger angle.
Evaluate the integral using any appropriate algebraic method or trigonometric
identity.
S-
dy
18 √2 (1+y2/3)
y
Chapter 7 Solutions
Finite Mathematics, Loose-leaf Version
Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - Prob. 7ECh. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - Prob. 9ECh. 7.1 - In Exercises 118, describe the sample space S of...
Ch. 7.1 - Prob. 11ECh. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - Prob. 14ECh. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - In Exercises 118, describe the sample space S of...Ch. 7.1 - A packet of gummy candy contains four strawberry...Ch. 7.1 - A bag contains three red marbles, two blue ones,...Ch. 7.1 - President Barack H. Obamas first cabinet consisted...Ch. 7.1 - Prob. 22ECh. 7.1 - Suppose two dice (one red, one green) are rolled....Ch. 7.1 - Suppose two dice (one red, one green) are rolled....Ch. 7.1 - Suppose two dice (one red, one green) are rolled....Ch. 7.1 - Prob. 26ECh. 7.1 - Suppose two dice (one red, one green) are rolled....Ch. 7.1 - Prob. 28ECh. 7.1 - Suppose two dice (one red, one green) are rolled....Ch. 7.1 - Suppose two dice (one red, one green) are rolled....Ch. 7.1 - Let W be the event that you will use the books...Ch. 7.1 - Prob. 32ECh. 7.1 - Let W be the event that you will use the books...Ch. 7.1 - Prob. 34ECh. 7.1 - Let W be the event that you will use the books...Ch. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - In Exercises 3942, Pablo randomly picks three...Ch. 7.1 - In Exercises 3942, Pablo randomly picks three...Ch. 7.1 - In Exercises 3942, Pablo randomly picks three...Ch. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Housing Prices Exercises 4348 are based on the map...Ch. 7.1 - Housing Prices Exercises 4348 are based on the map...Ch. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Publishing Exercises 4956 are based on the...Ch. 7.1 - Publishing Exercises 4956 are based on the...Ch. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Publishing Exercises 4956 are based on the...Ch. 7.1 - Publishing Exercises 4956 are based on the...Ch. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Stocks Exercises 5762 are based on the following...Ch. 7.1 - Prob. 61ECh. 7.1 - Prob. 62ECh. 7.1 - Prob. 63ECh. 7.1 - Animal Psychology Exercises 6368 concern the...Ch. 7.1 - Animal Psychology Exercises 6368 concern the...Ch. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Exercises 6972 use counting arguments from the...Ch. 7.1 - Exercises 6972 use counting arguments from the...Ch. 7.1 - Exercises 6972 use counting arguments from the...Ch. 7.1 - Exercises 6972 use counting arguments from the...Ch. 7.1 - Prob. 73ECh. 7.1 - Prob. 74ECh. 7.1 - Prob. 75ECh. 7.1 - Prob. 76ECh. 7.1 - Prob. 77ECh. 7.1 - Prob. 78ECh. 7.1 - Prob. 79ECh. 7.1 - Prob. 80ECh. 7.1 - Prob. 81ECh. 7.1 - Prob. 82ECh. 7.1 - Prob. 83ECh. 7.1 - Prob. 84ECh. 7.2 - In Exercises 16, calculate the relative frequency...Ch. 7.2 - Prob. 2ECh. 7.2 - In Exercises 16, calculate the relative frequency...Ch. 7.2 - In Exercises 16, calculate the relative frequency...Ch. 7.2 - In Exercises 16, calculate the relative frequency...Ch. 7.2 - In Exercises 16, calculate the relative frequency...Ch. 7.2 - Exercises 712 are based on the following table,...Ch. 7.2 - Exercises 712 are based on the following table,...Ch. 7.2 - Exercises 712 are based on the following table,...Ch. 7.2 - Exercises 712 are based on the following table,...Ch. 7.2 - Exercises 712 are based on the following table,...Ch. 7.2 - Exercises 712 are based on the following table,...Ch. 7.2 - In Exercises 1318, say whether the given...Ch. 7.2 - Prob. 14ECh. 7.2 - In Exercises 1318, say whether the given...Ch. 7.2 - In Exercises 1318, say whether the given...Ch. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - In Exercises 19 and 20, complete the given...Ch. 7.2 - In Exercises 19 and 20, complete the given...Ch. 7.2 - Exercises 2124 require the use of a calculator or...Ch. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Exercises 2124 require the use of a calculator or...Ch. 7.2 - Latin Music Sales: 2013 In a survey of 500 Latin...Ch. 7.2 - Latin Music Sales: 2009 In a survey of 400 Latin...Ch. 7.2 - Prob. 27ECh. 7.2 - Subprime Mortgages during the 20002008 Housing...Ch. 7.2 - Population Age in Mexico The following table shows...Ch. 7.2 - Population Age in the United States The following...Ch. 7.2 - Prob. 31ECh. 7.2 - Motor Vehicle Safety The following table shows...Ch. 7.2 - Prob. 33ECh. 7.2 - Internet Connections The following pie chart shows...Ch. 7.2 - Stock Market Gyrations The following chart shows...Ch. 7.2 - Stock Market Gyrations Repeat Exercise 35 using...Ch. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Publishing Exercises 3746 are based on the...Ch. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Publishing Exercises 3746 are based on the...Ch. 7.2 - Publishing Exercises 3746 are based on the...Ch. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Organic Produce A 2001 Agriculture Department...Ch. 7.2 - Organic Produce Repeat Exercise 49 using the...Ch. 7.2 - Steroids Testing A pharmaceutical company is...Ch. 7.2 - Lie Detectors A manufacturer of lie detectors is...Ch. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.3 - Complete the following probability distribution...Ch. 7.3 - Repeat Exercise 1 using the following table....Ch. 7.3 - In Exercises 38, calculate the (modeled)...Ch. 7.3 - In Exercises 38, calculate the (modeled)...Ch. 7.3 - In Exercises 38, calculate the (modeled)...Ch. 7.3 - In Exercises 38, calculate the (modeled)...Ch. 7.3 - Prob. 7ECh. 7.3 - In Exercises 38, calculate the (modeled)...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - Prob. 13ECh. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - In Exercises 918 an experiment is given together...Ch. 7.3 - Prob. 19ECh. 7.3 - If two indistinguishable dice are rolled, what is...Ch. 7.3 - A die is weighted in such a way that each of 2, 4,...Ch. 7.3 - Another die is weighted in such a way that each of...Ch. 7.3 - A tetrahedral die has four faces, numbered 14. If...Ch. 7.3 - Adodecahedraldiehas12faces, numbered112. If the...Ch. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - Prob. 29ECh. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - Prob. 31ECh. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - Prob. 36ECh. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - In Exercises 2540, use the given information to...Ch. 7.3 - In Exercises 4146, determine whether the...Ch. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - In Exercises 4146, determine whether the...Ch. 7.3 - Prob. 46ECh. 7.3 - Subprime Mortgages during the 20002008 Housing...Ch. 7.3 - Subprime Mortgages during the 20002008 Housing...Ch. 7.3 - Ethnic Diversity The following pie chart shows the...Ch. 7.3 - Ethnic Diversity (Compare Exercise 49.) The...Ch. 7.3 - Internet Investments in the 1990s The following...Ch. 7.3 - Internet Investments in the 1990s The following...Ch. 7.3 - Market Share: Light Vehicles In 2003, 25% of all...Ch. 7.3 - Market Share: Light Vehicles In 2000, 15% of all...Ch. 7.3 - Gambling In Exercises 5562 are detailed some of...Ch. 7.3 - Gambling In Exercises 5562 are detailed some of...Ch. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Gambling In Exercises 5562 are detailed some of...Ch. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Astrology The astrology software package Turbo...Ch. 7.3 - Astrology Another astrology software package, Java...Ch. 7.3 - Polls According to a New York Times/CBS poll...Ch. 7.3 - Polls According to The New York Times/CBS poll of...Ch. 7.3 - Electric Car Sales In 2014 the probability that a...Ch. 7.3 - Hybrid Auto Sales In 2010 the probability that a...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Student Admissions Exercises 6984 are based on the...Ch. 7.3 - Social Security According to The New York...Ch. 7.3 - Prob. 86ECh. 7.3 - Prob. 87ECh. 7.3 - Swords and Sorcery Lance the Wizard has been...Ch. 7.3 - Public Health A study shows that 80% of the...Ch. 7.3 - Public Health A study shows that 75% of the...Ch. 7.3 - Prob. 91ECh. 7.3 - Prob. 92ECh. 7.3 - Prob. 93ECh. 7.3 - Prob. 94ECh. 7.3 - Prob. 95ECh. 7.3 - Prob. 96ECh. 7.3 - Prob. 97ECh. 7.3 - Prob. 98ECh. 7.3 - Prob. 99ECh. 7.3 - Prob. 100ECh. 7.3 - Prob. 101ECh. 7.3 - Prob. 102ECh. 7.3 - Prob. 103ECh. 7.3 - Prob. 104ECh. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Recall from Example 1 that whenever Suzan sees a...Ch. 7.4 - Dogs of the Dow The Dogs of the Dow are the stocks...Ch. 7.4 - Dogs of the Dow The Dogs of the Dow are the stocks...Ch. 7.4 - Dogs of the Dow The Dogs of the Dow are the stocks...Ch. 7.4 - Dogs of the Dow The Dogs of the Dow are the stocks...Ch. 7.4 - Dogs of the Dow The Dogs of the Dow are the stocks...Ch. 7.4 - Dogs of the Dow The Dogs of the Dow are the stocks...Ch. 7.4 - Prob. 17ECh. 7.4 - Tests A test has three parts. Part A consists of...Ch. 7.4 - Poker In Exercises 1924 you are asked to calculate...Ch. 7.4 - Poker In Exercises 1924 you are asked to calculate...Ch. 7.4 - Prob. 21ECh. 7.4 - Poker In Exercises 1924 you are asked to calculate...Ch. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - The Monkey at the Typewriter Suppose that a monkey...Ch. 7.4 - The Cat on the Piano A standard piano keyboard has...Ch. 7.4 - Prob. 27ECh. 7.4 - (Based on a question from the GMAT) Tyler and...Ch. 7.4 - Lotteries The Sorry State Lottery requires you to...Ch. 7.4 - Lotteries The Sad State Lottery requires you to...Ch. 7.4 - Transfers Your company is considering offering 400...Ch. 7.4 - Transfers (Refer back to Exercise 31.) After...Ch. 7.4 - Lotteries In a New York State daily lottery game,...Ch. 7.4 - Lotteries Refer back to Exercise 33. Find the...Ch. 7.4 - Elimination Tournaments In an elimination...Ch. 7.4 - Elimination Tournaments In a (fictitious) soccer...Ch. 7.4 - Elimination Tournaments The following diagram...Ch. 7.4 - Elimination Tournaments The following diagram...Ch. 7.4 - Elimination Tournaments The following diagram...Ch. 7.4 - Elimination Tournaments The following diagram...Ch. 7.4 - Sports The following table shows the results of...Ch. 7.4 - Prob. 42ECh. 7.4 - Graph Searching A graph consists of a collection...Ch. 7.4 - Prob. 44ECh. 7.4 - Product Design Your company has patented an...Ch. 7.4 - Prob. 46ECh. 7.4 - Committees An investigatory committee in the...Ch. 7.4 - Committees A committee is to consist of a chair,...Ch. 7.4 - Prob. 49ECh. 7.4 - What is wrong with the following argument? When we...Ch. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7.4 - Prob. 53ECh. 7.4 - Prob. 54ECh. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - Prob. 3ECh. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - Prob. 9ECh. 7.5 - In Exercises 110, compute the indicated quantity....Ch. 7.5 - In Exercises 1116, fill in the blanks using the...Ch. 7.5 - In Exercises 1116, fill in the blanks using the...Ch. 7.5 - Prob. 13ECh. 7.5 - In Exercises 1116, fill in the blanks using the...Ch. 7.5 - In Exercises 1116, fill in the blanks using the...Ch. 7.5 - In Exercises 1116, fill in the blanks using the...Ch. 7.5 - In Exercises 1722, find the conditional...Ch. 7.5 - In Exercises 1722, find the conditional...Ch. 7.5 - Prob. 19ECh. 7.5 - In Exercises 1722, find the conditional...Ch. 7.5 - Prob. 21ECh. 7.5 - In Exercises 1722, find the conditional...Ch. 7.5 - Exercises 2328 require the use of counting...Ch. 7.5 - Exercises 2328 require the use of counting...Ch. 7.5 - Exercises 2328 require the use of counting...Ch. 7.5 - Exercises 2328 require the use of counting...Ch. 7.5 - Exercises 2328 require the use of counting...Ch. 7.5 - Exercises 2328 require the use of counting...Ch. 7.5 - Prob. 29ECh. 7.5 - In Exercises 2932, supply the missing quantities....Ch. 7.5 - In Exercises 2932, supply the missing quantities....Ch. 7.5 - In Exercises 2932, supply the missing quantities....Ch. 7.5 - In Exercises 3336, say whether the given pair of...Ch. 7.5 - In Exercises 3336, say whether the given pair of...Ch. 7.5 - In Exercises 3336, say whether the given pair of...Ch. 7.5 - In Exercises 3336, say whether the given pair of...Ch. 7.5 - Prob. 37ECh. 7.5 - In Exercises 3742, two dice (one red and one...Ch. 7.5 - In Exercises 3742, two dice (one red and one...Ch. 7.5 - In Exercises 3742, two dice (one red and one...Ch. 7.5 - Prob. 41ECh. 7.5 - In Exercises 3742, two dice (one red and one...Ch. 7.5 - If a coin is tossed 11 times, find the probability...Ch. 7.5 - Prob. 44ECh. 7.5 - Personal Bankruptcy In 2004 the probability that a...Ch. 7.5 - Personal Bankruptcy In 2004 the probability that a...Ch. 7.5 - Existing Home Sales During the year ending April...Ch. 7.5 - Existing Home Sales Refer to the data given in...Ch. 7.5 - Prob. 49ECh. 7.5 - Social Security According to The New York...Ch. 7.5 - Prob. 51ECh. 7.5 - Marketing A market survey shows that 60% of the...Ch. 7.5 - Prob. 53ECh. 7.5 - Prob. 54ECh. 7.5 - Publishing Exercises 5562 are based on the...Ch. 7.5 - Publishing Exercises 5562 are based on the...Ch. 7.5 - Prob. 57ECh. 7.5 - Publishing Exercises 5562 are based on the...Ch. 7.5 - Publishing Exercises 5562 are based on the...Ch. 7.5 - Publishing Exercises 5562 are based on the...Ch. 7.5 - Publishing Exercises 5562 are based on the...Ch. 7.5 - Publishing Exercises 5562 are based on the...Ch. 7.5 - Prob. 63ECh. 7.5 - Prob. 64ECh. 7.5 - In Exercises 6368, draw an appropriate tree...Ch. 7.5 - In Exercises 6368, draw an appropriate tree...Ch. 7.5 - Prob. 67ECh. 7.5 - Prob. 68ECh. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Education and Employment Exercises 6978 are based...Ch. 7.5 - Air Bag Safety According to a 2000 study conducted...Ch. 7.5 - Air Bag Safety According to the study cited in...Ch. 7.5 - Prob. 81ECh. 7.5 - Prob. 82ECh. 7.5 - Internet Use in 2000 The following pie chart shows...Ch. 7.5 - Internet Use in 2001 Repeat Exercise 83 using the...Ch. 7.5 - Auto Theft Exercises 8590 are based on the...Ch. 7.5 - Prob. 86ECh. 7.5 - Prob. 87ECh. 7.5 - Auto Theft Exercises 8590 are based on the...Ch. 7.5 - Prob. 89ECh. 7.5 - Prob. 90ECh. 7.5 - Drug Tests If 90% of the athletes who test...Ch. 7.5 - Fitness Tests If 80% of candidates for the soccer...Ch. 7.5 - Prob. 93ECh. 7.5 - Food Safety According to the study mentioned in...Ch. 7.5 - Prob. 95ECh. 7.5 - Prob. 96ECh. 7.5 - Ultimate Hockey Cyber Video Games, Inc., the...Ch. 7.5 - Ultimate Hockey (See Exercise 97.) Cyber Video...Ch. 7.5 - The probability of misspelling Waner is p and is...Ch. 7.5 - The probability of spelling Waner correctly is p,...Ch. 7.5 - Prob. 101ECh. 7.5 - Name three pairs of independent events when a pair...Ch. 7.5 - Prob. 103ECh. 7.5 - Prob. 104ECh. 7.5 - Prob. 105ECh. 7.5 - Prob. 106ECh. 7.5 - Prob. 107ECh. 7.5 - Prob. 108ECh. 7.5 - Prob. 109ECh. 7.5 - Prob. 110ECh. 7.5 - Prob. 111ECh. 7.5 - Prob. 112ECh. 7.6 - In Exercises 18, use Bayes theorem or a tree...Ch. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - In Exercises 18, use Bayes theorem or a tree...Ch. 7.6 - In Exercises 18, use Bayes theorem or a tree...Ch. 7.6 - In Exercises 18, use Bayes theorem or a tree...Ch. 7.6 - Prob. 7ECh. 7.6 - In Exercises 18, use Bayes theorem or a tree...Ch. 7.6 - Music Downloading According to a study on the...Ch. 7.6 - Music Downloading According to the study cited in...Ch. 7.6 - Weather It snows in Greenland an average of once...Ch. 7.6 - Weather It rains in Spain an average of once every...Ch. 7.6 - University Admissions In fall 2014, 34% of...Ch. 7.6 - University Admissions In fall 2014, 71% of...Ch. 7.6 - Side-Impact Hazard In 2004, 45.4% of all light...Ch. 7.6 - Side-Impact Hazard In 2004, 27.3% of all light...Ch. 7.6 - Athletic Fitness Tests Any athlete who fails the...Ch. 7.6 - Academic Testing Professor Frank Nabarro insists...Ch. 7.6 - Side-Impact Hazard (Compare Exercise 15.) In 2004,...Ch. 7.6 - Side-Impact Hazard In 1986, 23.9% of all light...Ch. 7.6 - University Admissions In fall 2008, UCLA admitted...Ch. 7.6 - Prob. 22ECh. 7.6 - Prob. 23ECh. 7.6 - Internet Use (Historical) In 2000, 59% of all...Ch. 7.6 - Market Surveys A New York Times survey of...Ch. 7.6 - Prob. 26ECh. 7.6 - Grade Complaints Two of the mathematics professors...Ch. 7.6 - Weather Prediction A local TV station employs...Ch. 7.6 - Employment in the 1980s In a 1987 survey of...Ch. 7.6 - Employment in the 1980s Repeat Exercise 29 in the...Ch. 7.6 - Prob. 31ECh. 7.6 - Prob. 32ECh. 7.6 - Benefits of Exercise According to a study in The...Ch. 7.6 - Prob. 34ECh. 7.6 - Air Bag Safety According to a 2000 study conducted...Ch. 7.6 - Prob. 36ECh. 7.6 - Prob. 37ECh. 7.6 - Prob. 38ECh. 7.6 - Prob. 39ECh. 7.6 - Prob. 40ECh. 7.6 - Prob. 41ECh. 7.6 - Write down an expanded form of Bayes theorem that...Ch. 7.6 - Prob. 43ECh. 7.6 - Politics Refer back to Exercise 43. If the letter...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - Prob. 9ECh. 7.7 - In Exercises 110, write down the transition matrix...Ch. 7.7 - In Exercises 1124, you are given a transition...Ch. 7.7 - In Exercises 1124, you are given a transition...Ch. 7.7 - Prob. 13ECh. 7.7 - In Exercises 1124, you are given a transition...Ch. 7.7 - In Exercises 1124, you are given a transition...Ch. 7.7 - In Exercises 1124, you are given a transition...Ch. 7.7 - Prob. 17ECh. 7.7 - Prob. 18ECh. 7.7 - Prob. 19ECh. 7.7 - In Exercises 1124, you are given a transition...Ch. 7.7 - Prob. 21ECh. 7.7 - Prob. 22ECh. 7.7 - Prob. 23ECh. 7.7 - Prob. 24ECh. 7.7 - In Exercises 2536, you are given a transition...Ch. 7.7 - In Exercises 2536, you are given a transition...Ch. 7.7 - Prob. 27ECh. 7.7 - Prob. 28ECh. 7.7 - Prob. 29ECh. 7.7 - In Exercises 2536, you are given a transition...Ch. 7.7 - In Exercises 2536, you are given a transition...Ch. 7.7 - Prob. 32ECh. 7.7 - Prob. 33ECh. 7.7 - Prob. 34ECh. 7.7 - In Exercises 2536, you are given a transition...Ch. 7.7 - Prob. 36ECh. 7.7 - Marketing A market survey shows that half the...Ch. 7.7 - Major Switching At Suburban Community College, 10%...Ch. 7.7 - Pest Control In an experiment to test the...Ch. 7.7 - Employment You have worked for the Department of...Ch. 7.7 - Prob. 41ECh. 7.7 - Debt Analysis A credit card company classifies its...Ch. 7.7 - Textbook Adoptions College instructors who adopt...Ch. 7.7 - Confidence Level Tommy the Dunkers performance on...Ch. 7.7 - Debt Analysis As the manager of a large retailing...Ch. 7.7 - Prob. 46ECh. 7.7 - Prob. 51ECh. 7.7 - Dissipation Consider the following five-state...Ch. 7.7 - Prob. 54ECh. 7.7 - Prob. 55ECh. 7.7 - Prob. 56ECh. 7.7 - Describe some drawbacks to using Markov processes...Ch. 7.7 - Prob. 58ECh. 7.7 - Prob. 59ECh. 7.7 - Prob. 60ECh. 7.7 - Prob. 61ECh. 7.7 - Prob. 62ECh. 7.7 - Prob. 63ECh. 7.7 - Prob. 64ECh. 7.7 - Prob. 65ECh. 7.7 - Prob. 66ECh. 7 - In Exercises 16, say how many elements are in the...Ch. 7 - In Exercises 16, say how many elements are in the...Ch. 7 - In Exercises 16, say how many elements are in the...Ch. 7 - In Exercises 16, say how many elements are in the...Ch. 7 - In Exercises 16, say how many elements are in the...Ch. 7 - In Exercises 16, say how many elements are in the...Ch. 7 - In Exercises 710, calculate the relative frequency...Ch. 7 - In Exercises 710, calculate the relative frequency...Ch. 7 - In Exercises 710, calculate the relative frequency...Ch. 7 - In Exercises 710, calculate the relative frequency...Ch. 7 - In Exercises 1114, calculate the probability P(E)....Ch. 7 - In Exercises 1114, calculate the probability P(E)....Ch. 7 - In Exercises 1114, calculate the probability P(E)....Ch. 7 - In Exercises 1114, calculate the probability P(E)....Ch. 7 - A bag contains four red marbles, two green ones,...Ch. 7 - Prob. 16RECh. 7 - A bag contains four red marbles, two green ones,...Ch. 7 - A bag contains four red marbles, two green ones,...Ch. 7 - A bag contains four red marbles, two green ones,...Ch. 7 - Prob. 20RECh. 7 - In Exercises 2126, find the probability of being...Ch. 7 - In Exercises 2126, find the probability of being...Ch. 7 - In Exercises 2126, find the probability of being...Ch. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Two dice, one green and one yellow, are rolled. In...Ch. 7 - Two dice, one green and one yellow, are rolled. In...Ch. 7 - Prob. 29RECh. 7 - Two dice, one green and one yellow, are rolled. In...Ch. 7 - Prob. 31RECh. 7 - Two dice, one green and one yellow, are rolled. In...Ch. 7 - A poll shows that half the consumers who use Brand...Ch. 7 - A poll shows that half the consumers who use Brand...Ch. 7 - A poll shows that half the consumers who use Brand...Ch. 7 - A poll shows that half the consumers who use Brand...Ch. 7 - Inventory OHaganBooks.com currently operates three...Ch. 7 - Prob. 38RECh. 7 - Inventory OHaganBooks.com currently operates three...Ch. 7 - Prob. 40RECh. 7 - Inventory OHaganBooks.com currently operates three...Ch. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Marketing To gauge the effectiveness of the...Ch. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Sales According to statistics gathered by...Ch. 7 - Prob. 52RECh. 7 - University Admissions In the year when Billy-Sean...Ch. 7 - Prob. 54RECh. 7 - Competition As was mentioned earlier,...Ch. 7 - Competition As was mentioned earlier,...Ch. 7 - Prob. 57RECh. 7 - Prob. 58RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- iid B1 Suppose X1, ..., Xn fx(x), where 2 fx(x) = x exp(−x²/0), 0<< (0 otherwise). (a) Find the maximum likelihood estimator of 0. (b) Show that the MLE is an unbiased estimator of 0. (c) Find the MSE of the MLE. Hint: For parts (b) and (c), you may use integration by parts.arrow_forward4. Suppose the demand for a certain item is given by D(p)=-2 p² - 4p+350, where p represents the price of the item in dollars. a) Find the rate of change of demand with respect to price. b) Find and interpret the rate of change of demand when the price is $11.arrow_forward√3-x, x≤3, 2. For f(x) = 1 find each of the following. x > 3, x-3' 1. f(-6) 2. f(3) 3. f(7) 3. Find the domain of each of the following functions.arrow_forward
- 1. Using the definition of the derivative, find f'(x). Then find f'(2), f'(0) and f'(3) when the derivative exists. a) f(x)=5x²-6x-1arrow_forward2. f(x)=√7-x 4. A manufacturer has a monthly fixed cost of $40,000 and a production cost of $8 for each unit produced. The product sells for $12 per unit. 1. What is the cost function? 2. What is the revenue function? 3. Compute the profit corresponding to 12,000 units. 5. A rectangular box is to have a square base and a volume of 20 ft3. The material for the base costs $0.30 per ft2, the material for the sides cost $0.10 per ft2, and the material for the top costs $0.20 per ft2. Letting x denote the length of one side of the base,arrow_forwardSolve using superposition principlearrow_forward
- review problems please help!arrow_forwardSolve the problems on the imagearrow_forward3. f(7) 3. Find the domain of each of the following functions. 1 1. f(x)=2-6x+8 2. f(x)=√√7-x 4. A manufacturer has a monthly fixed cost of $40,000 and a production cost of $8 for each unit produced. The product sells for $12 per unit.arrow_forward
- 7. Evaluate the following limits and justify each step. (a) lim (3x²+2x+1) 1 x²+4x-12 (b) lim 1 2 x² - 2x t-√√3t+4 (c) lim t-0 4-t x²-6x+5 (d) lim (e) lim x 5 x-5 x→2 x²+2x+3 4u+1-3 (f) lim u➡2 u-2 1 (g) lim x-3 2 x 55 x - 7x4 +4 (h) lim xx 5x+2x-1 x+1 (i) lim x²-2x+5 - 7x8+4x7 +5xarrow_forward6. Given the following graph f(x). (-2,2) 2- -5 -3 -2 (-2,-1) -1 (0,1) -2- 1 (3,0) 2 3 4 5 (3,-1) א X Compute each of the following. (a) f(-2) (b) lim f(x) #129 (c) lim f(x) *→12+ (d) lim f(x) 811H (e) f(0) (f) lim f(x) 8011 (m) Is the function continuous at x = -2,0,3? Why or why not? (g) lim f(x) +0x (h) lim f(x) x 0 (i) f(3) (j) lim f(x) x-3- (k) lim f(x) x+3+ (1) lim f(x) #13arrow_forward(i) For a given constant a > 0, let an investor's preference be represented by the Gaussian utility function U(w)=1-e-aw² For what range of wealth level w will the investor be non-satiated and risk-averse? Explain your answer. (ii) Give an example of a utility function that exhibits DARA and verify it. (iii) Determine the class of utility functions with relative risk aversion coefficient R(w)= w², w> 0.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Find number of persons in a part with 66 handshakes Combinations; Author: Anil Kumar;https://www.youtube.com/watch?v=33TgLi-wp3E;License: Standard YouTube License, CC-BY
Discrete Math 6.3.1 Permutations and Combinations; Author: Kimberly Brehm;https://www.youtube.com/watch?v=J1m9sB5XZQc;License: Standard YouTube License, CC-BY
How to use permutations and combinations; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=NEGxh_D7yKU;License: Standard YouTube License, CC-BY
Permutations and Combinations | Counting | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=0NAASclUm4k;License: Standard Youtube License
Permutations and Combinations Tutorial; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=XJnIdRXUi7A;License: Standard YouTube License, CC-BY