
a.
To graph: The solid's volume created by rotating the area defined by the
a.
Explanation of Solution
Given Information: To determine the solid's formed by rotating volume
Graph: To get the solid's volume created by rotating the area in the
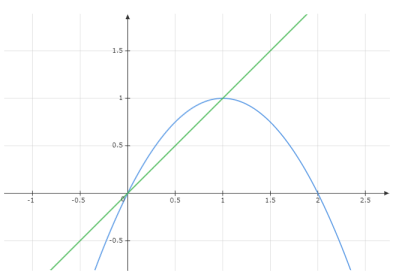
It then rotates about the

The volume calculation formula.
The graph above resembles a cylindrical shell when it rotates at the
Remember the location of the cylinder-shaped shell.
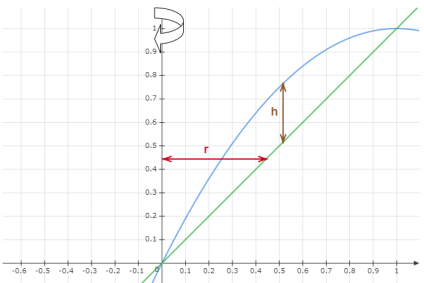
To start, locate the intersections. In place of equation
Then use factoring to determine the values of
The points of the
Substitute the
The points of intersection are
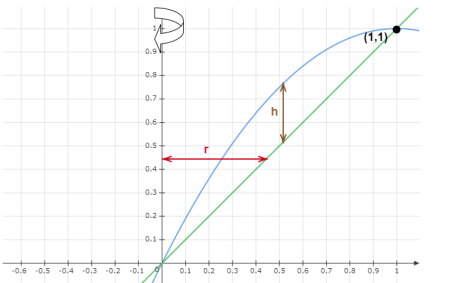
A little area around the cylindrical shell in the graph must be used to solve the volume problem.
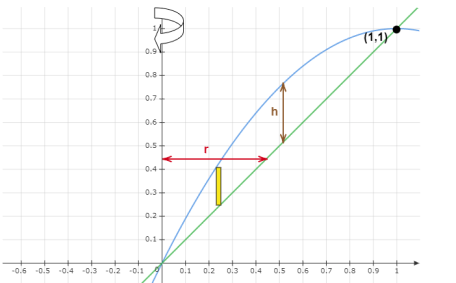
Substitute equation (4) to equation (3).
\
The interval
Integrate after applying the distributive property.
Substitute the results of the above calculation.
b.
To graph: To determine the solid's volume created by rotating the area around constrained by
b.
Explanation of Solution
Given Information: To calculate the volume of the solid produced by rotating the area at the line
Graph: The previous equation
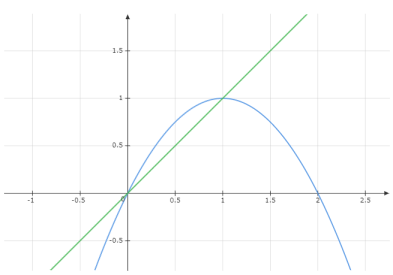
It then rotates at line
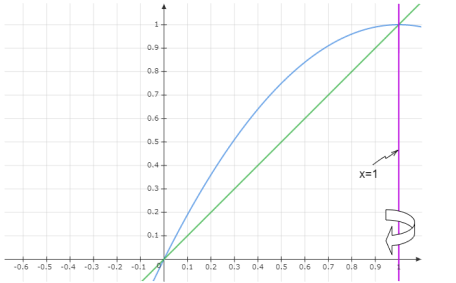
Remember the volume formula.
The graph above resembles a cylindrical shell when it rotates at the
Remember the location of the cylinder-shaped shell.
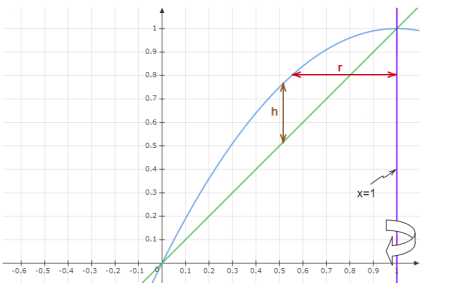
Find the junction point or points first. In place of equation
Then use factoring to determine the values of
The points
Then modify equation by substituting the
Consequently,
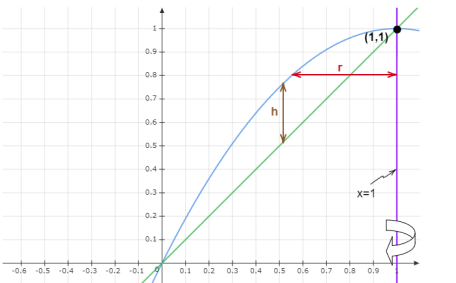
A little section of the graph's cylindrical shell area can be used to solve the volume problem.
Substitute equation
See how the interval
Integrate after applying the distributive property.
After that, swap out the values from the previous result.
Consequently, the volume is
Chapter 7 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- Let f be a function whose graph consists of 5 line segments and a semicircle as shown in the figure below. Let g(x) = √ƒƒ(t) dt . 0 3 2 -2 2 4 5 6 7 8 9 10 11 12 13 14 15 1. g(0) = 2. g(2) = 3. g(4) = 4. g(6) = 5. g'(3) = 6. g'(13)=arrow_forwardThe expression 3 | (3+1/+1) of the following integrals? A Ов E + + + + 18 3+1+1 3++1 3++1 (A) √2×14 dx x+1 (C) 1½-½√ √ ² ( 14 ) d x (B) √31dx (D) So 3+x -dx is a Riemann sum approximation of which 5 (E) 1½√√3dx 2x+1arrow_forward2. Suppose the population of Wakanda t years after 2000 is given by the equation f(t) = 45000(1.006). If this trend continues, in what year will the population reach 50,000 people? Show all your work, round your answer to two decimal places, and include units. (4 points)arrow_forward
- 3. Solve the equation, give the answer exactly (no calculator approximations), and show all your work. (4 points) log5 2x = 3arrow_forwardLet I = f(x) dx, where f is the function whose graph is shown. 4 2 y f X 1 2 3 4 (a) Use the graph to find L2, R2 and M2. R₂ M2 = = = (b) Are these underestimates or overestimates of I? O 42 is an underestimate. O 42 is an overestimate. ◇ R2 is an underestimate. OR2 is an overestimate. OM2 is an underestimate. ○ M2 is an overestimate. (c) Use the graph to find T2. T₂ =arrow_forwardVector u has a magnitude of 23 and vector v has a magnitude of 83. The angle between the two vectors is 126 degrees.a) Draw a fully-labelled vector diagram showing the two vectors and the resultant vector when they are added together.b) Find the magnitude of the resultant vector.c) Find the direction of the resultant vector relative to vector u. Solding by finding the x and y of the vectors and addingarrow_forward
- 3) If a is a positive number, what is the value of the following double integral? 2a Love Lv 2ay-y² .x2 + y2 dadyarrow_forward16. Solve each of the following equations for x. (a) 42x+1 = 64 (b) 27-3815 (c) 92. 27² = 3-1 (d) log x + log(x - 21) = 2 (e) 3 = 14 (f) 2x+1 = 51-2xarrow_forward11. Find the composition fog and gof for the following functions. 2 (a) f(x) = 2x+5, g(x) = x² 2 (b) f(x) = x²+x, g(x) = √√x 1 (c) f(x) = -1/2) 9 9(x) = х = - Xarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





