Chapter 7.5, Problem 14E

$\text{(a)}$

To determine

To explain: How to approximate to force against the end of the tank by the Riemann sum.

Answer to Problem 14E

The answer is:

Explanation of Solution

Given information:

The vertical end of the tank contained water weight $62.4\text{lb}/{\text{ft}}^3$ has the given shape.

The figure is:

  

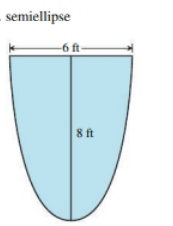
Calculation:

Let's first review the equation for a fluid force in a constant-depth surface in order to determine the force acting against the end of the tank.

  $\begin{array}{c}F=pA\\ =whA\end{array}$

Where,

  $\begin{array}{c}p=\text{ pressure }\\ A=\text{ area }\\ w=\text{ weight-density }\\ h=\text{ height }\end{array}$

in order to approximate the force using Riemann sum, let divide the height of the of the tank into $k$ -partitions. Since the tank is a semi-ellipse, then this implies that

  $\begin{array}{c}a=8\\ b-3\end{array}$

Now assume that the centre of the semi-ellipse is $(0,0)$ and obtain its equation.

  $\begin{array}{c}\frac{y^2}{{(8)}^2}+\frac{x^2}{{(3)}^2}=1\\ \Rightarrow \frac{y^2}{{(8)}^2}=1-\frac{x^2}{{(3)}^2}\\ \Rightarrow y^2=8^2\left(1-\frac{x^2}{{(3)}^2}\right)\\ =64\left(1-\frac{x^2}{9}\right)\\ \Rightarrow y=\sqrt{64\left(1-\frac{x^2}{9}\right)}\end{array}$

Put the tank in the plane of cartesian coordinates will allow us to draw one strip as seen below.

  

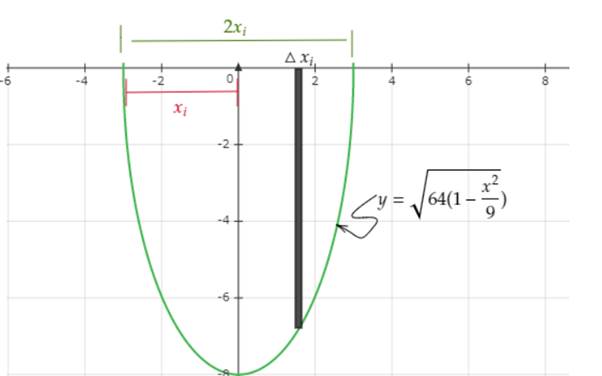
Where,

  $\begin{array}{c}2x_i=\text{ strip depth }\\ \sqrt{9-x^2}=\text{ strip length }\\ \text{Δ}x=\text{ width of the strip}\end{array}$

Now, The Riemann sum formula for the force is given below.

To generate the force approximation, substitute the value from the graph into equation $(1)$ along with the weight-density specified in the issue $\left(62.4lb/f{t}^3\right)$:

$\text{(b)}$

To determine

To find: The force as an integral.

Answer to Problem 14E

The answer: $2295.2lb$

Explanation of Solution

Given information:

The vertical end of the tank contained water weight $62.4\text{lb}/{\text{ft}}^3$ has the given shape.

The figure is:

  

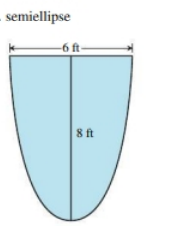
Calculation:

Have a look at the graph above. The y-axis of the graph is symmetric, as can be seen. multiply by two and integrate the right side using the same strip. Put the integral together,

  

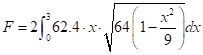
Now let,

  $\begin{array}{c}u=\left(1-\frac{x^2}{9}\right)\\ du=-\frac{2x}{9}dx\\ xdx=-\frac{9du}{2}\end{array}$

New boundaries of integration:

Upper boundary:

  $\begin{array}{c}x=3\\ \to u=\left(1-\frac{3^2}{9}\right)\\ =0\end{array}$

Lower boundary:

  $\begin{array}{c}x=0\\ \to u=\left(1-\frac{{(0)}^2}{9}\right)\\ =1\end{array}$

Put everything to the integration:

  

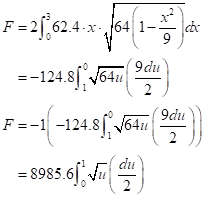
Now evaluate the integral:

  

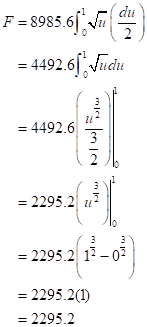
Therefore, the required force as an integral is $2295.2lb$ .