Chapter 7.2, Problem 31E

To determine

To find: The area of the region enclosed by the lines and curve.

Answer to Problem 31E

The area is: $A=\frac{4}{\pi }-1$

Explanation of Solution

Given information:

The curves are:

  $\begin{array}{c}y=\sin (\pi x/2)\\ y=x\end{array}$

Calculation:

To find the area of the region which is enclosed by the curves are:

  $\begin{array}{c}y=\sin (\pi x/2)\mathrm{.....}(1)\\ y=x\mathrm{.....}(2)\end{array}$

Find the intersection points, i.e. the limits of integrations. Therefore, equalize the $(1)$ and $(2)$ .

This equation $(1)=(2)$ cannot be solve to use the elementary methods, so use the program Geogebra. Therefore, see on the picture of area of the region is enclosed by $(1)$ and $(2)$ .

From $x=-1$

To

  $x=0$

And from

  $x=0$

To

  $x=1$ .

Hence, the area is:

  

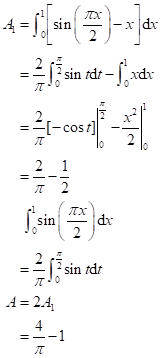
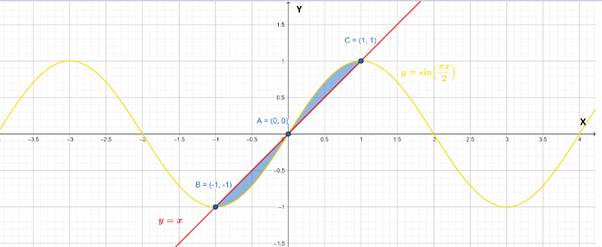
The graph is shown below:

  

Therefore, the required area of the region enclosed by the lines and curve is $\frac{4}{\pi }-1$ .