Chapter 7.3, Problem 109E

Solution

a.

To calculate: The characteristic polynomial $C\left(x\right)$ .

  $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$

The polynomial is $C\left(x\right)=x^2-8x+13$ .

Given Information:

The matrix is $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$.

Calculation:

Consider the given matrix,

  $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$

Polynomial is defined as,

  $C\left(x\right)=\det \left(x{I}_2-A\right)$

Substitute the values and find $x{I}_2-A$ .

  $\begin{array}{c}x{I}_2-A=x\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]-\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]\\ =\left[\begin{array}{cc}x& 0\\ 0& x\end{array}\right]-\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]\\ =\left[\begin{array}{cc}x-3& -2\\ -1& x-5\end{array}\right]\end{array}$

Find the determinant.

  $\begin{array}{c}C\left(x\right)=\det \left(x{I}_2-A\right)\\ =\left|\begin{array}{cc}x-3& -2\\ -1& x-5\end{array}\right|\\ =\left(x-5\right)\left(x-3\right)-2\\ =x^2-8x+13\end{array}$

Therefore, the obtained function is $C\left(x\right)=x^2-8x+13$ .

b.

To graph: The function $C\left(x\right)=x^2-8x+13$ as $y=C\left(x\right)$ .

The required graph is shown as below,

  

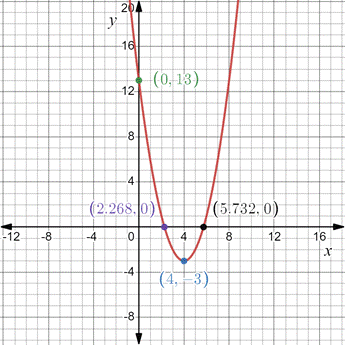
Given Information:

The function is $C\left(x\right)=x^2-8x+13$ .

Explanation:

Consider the given information,

  $C\left(x\right)=x^2-8x+13$

Find the intercept of the function by using 0 for x and 0 for y one by one.

  $\begin{array}{c}y=0^2-8\left(0\right)+13\\ =13\end{array}$

And,

  $\begin{array}{c}{x}^2-8x+13=0\\ x=\frac{8\pm \sqrt{64-4\left(13\right)\left(1\right)}}{2}\\ =\frac{8\pm \sqrt{12}}{2}\\ =\text{5}\text{.732},\text{2}\text{.268}\end{array}$

And,

  $\begin{array}{c}C\left(x\right)=x^2-8x+16-3\\ ={\left(x-4\right)}^2-3\end{array}$

The vertex is $\left(4,-3\right)$ .

Now, make the graph.

  

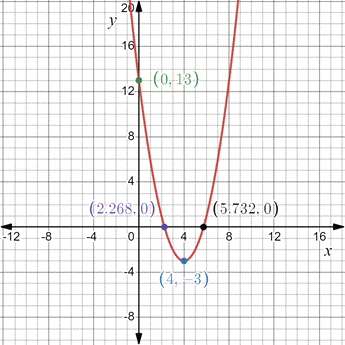
Therefore, the required graph is above graph.

c.

To calculate: The Eigen values of the given matrix $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$.

Eigen values are $4+\sqrt{3}$ and $4-\sqrt{3}$ .

Given Information:

The matrix is $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$.

Calculation:

Consider the given information,

  $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$

Now, find the Eigen values.

  $\begin{array}{r}\det \left(A-\lambda I\right)=0\\ \det \left(\left[\begin{array}{cc}3-\lambda & 2\\ 1& 5-\lambda \end{array}\right]\right)=0\\ \left(3-\lambda \right)\left(5-\lambda \right)-2=0\\ {\lambda }^2-8\lambda +13=0\end{array}$

And the root can be taken form the previous part (b).

  $4+\sqrt{3},4-\sqrt{3}$

Therefore, the Eigen values are $4+\sqrt{3}$ and $4-\sqrt{3}$ .

d.

To determine: The compression between determinant of the given matrix and the y -intercept.

The value of $\det A$ and the y -intercept is 13.

Given Information:

The matrix is $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$.

Calculation:

Consider the given information,

  $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$

Now, find the determinant.

  $\begin{array}{c}\det \left(\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]\right)=\left|\begin{array}{cc}3& 2\\ 1& 5\end{array}\right|\\ =5\left(3\right)-1\left(2\right)\\ =15-2\\ =13\end{array}$

And, the y -intercept is 13.

Therefore, the both the values are equal.

e.

To determine: The comparison between the sum of the main diagonal elements of A with the sum of the eigenvalues.

The main diagonal elements of A with the sum is equal to the sum of the eigenvalues.

Given Information:

The matrix is $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$.

Calculation:

Consider the given information,

  $A=\left[\begin{array}{cc}3& 2\\ 1& 5\end{array}\right]$

Now, find the sum of diagonal entries of the matrix.

  $\begin{array}{c}{a}_{11}+a_{22}=3+5\\ =8\end{array}$

Refer the Eigen values form the previous part and add them.

  $\begin{array}{c}4+\sqrt{3}+4-\sqrt{3}=4+4\\ =8\end{array}$

Therefore, the both the values are equal.